Матем. модели законов природы, из к-рых получаются ур-ния, описывающие любое физ. явление, не зависят от выбора системы мер. Поэтому ур-ния, описывающие фнз. явления, можно привести к безразмерному виду путём введения нек-рых характерных значений для каждого из определяющих физ. параметров. Тогда безразмерные коэф. новой безразмерной системы ур-ний, составленные из определяющих физ. параметров, и будут П. к. рассматриваемого явления (процесса). Величины П. к. зависят от выбора характерных значений определяющих параметров.
Так, в ур-нии 2-го закона Ньютона F = mw определяющими движение тела физ. параметрами являются действующая на движущееся тело сила F, масса тела т, длина пути l и время t (w = d2l/dt2 - ускорение тела). Обозначив чертой сверху безразмерные переменные, отнесённые к нек-рым характерным значениям F, m, l, t, получим безразмерное ур-ние
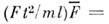
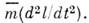 Коэф. Ft2/ml = Ne в левой части ур-ния является П. к.
механич. движения и наз. числом Ньютона.
Коэф. Ft2/ml = Ne в левой части ур-ния является П. к.
механич. движения и наз. числом Ньютона.
Когда ур-ния, описывающие физ. явление, неизвестны, П. к. отыскиваются при помощи анализа размерностей определяющих физ. параметров. Напр., состояние движения вязкой жидкости в цилиндрич. трубе определяется четырьмя параметрами: плотностью
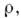 скоростью v, вязкостью жидкости
скоростью v, вязкостью жидкости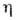 и диаметром трубы d. Из четырёх параметров можно составить только
одно безразмерное число - Рейнолъдса число
и диаметром трубы d. Из четырёх параметров можно составить только
одно безразмерное число - Рейнолъдса число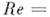
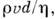 к-рое
и является П. к. рассматриваемого движения. Каждый из П. к. имеет свой
физ. смысл, как величина, пропорц. отношению однотипных физ. величин. Из
записи числа Re в виде
к-рое
и является П. к. рассматриваемого движения. Каждый из П. к. имеет свой
физ. смысл, как величина, пропорц. отношению однотипных физ. величин. Из
записи числа Re в виде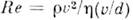 следует, что числитель пропорционален динамич. напору потока (силам инерции),
а знаменатель - силам вязкого (молекулярного) трения.
следует, что числитель пропорционален динамич. напору потока (силам инерции),
а знаменатель - силам вязкого (молекулярного) трения.
П. к. используются при моделировании и установлении общих фпз. закономерностей (критериальных зависимостей) в теории упругости, гпдроаэромеханике, теплофизике, электротехнике и электродинамике, магн. гидродинамике и др. областях физики.
При изучении упругих деформаций конструкции под воздействием внеш. сил осн. П. к. являются коэф. Пуассона для материала конструкции
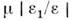 и критерии
и критерии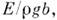 F/Eb2, где
F/Eb2, где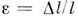 - относит. продольная деформация,
- относит. продольная деформация,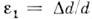 - относит. поперечная деформация, Е - модуль Юнга (см. Модули
упругости),
- относит. поперечная деформация, Е - модуль Юнга (см. Модули
упругости),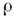 - плотность
материала конструкции, F - характерная внеш. сила,
b - характерный
размер конструкции, g - ускорение свободного падения.
- плотность
материала конструкции, F - характерная внеш. сила,
b - характерный
размер конструкции, g - ускорение свободного падения.
В процессах, изменяющихся с течением времени t, осн. П. к., характеризующим одинаковость протекания процессов во времени, является критерий гомохронности Но = vt/l.
При изучении гидроаэромеханич. процессов, теплопередачи и массопередачи различают П. к. в виде безразмерных постоянных, характеризующих вещество (среду), и П. к., связанные с переносом импульса, теплоты или массы. П. к., характеризующие вещество: Прандтля число Рr = v/а, Шмидта число Sc = v/D, Льюиса число Le = a/D, а также отношение уд. теплоёмкостей при пост. давлении и пост. объёме
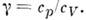 Здесь
Здесь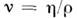 - коэф. кннематич. вязкости, а =
- коэф. кннематич. вязкости, а =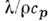 - коэф. температуропроводности,
- коэф. температуропроводности,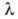 - коэф. теплопроводности, D - коэф. диффузии.
- коэф. теплопроводности, D - коэф. диффузии.
П. к., связанные с переносом импульса: Рейнольдса число Re = vl/v, Эйлера число
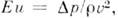 Фруда число Fr = v2/gl, число Вебера
Фруда число Fr = v2/gl, число Вебера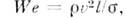 Маха
число М = v/c, Кнудсена число
Маха
число М = v/c, Кнудсена число и
Струхаля
число Sh = lf/v, являющееся критерием гомохронности в гидроаэромеханике.
При изучении нек-рых процессов удобно пользоваться также Архимеда числом
и
Струхаля
число Sh = lf/v, являющееся критерием гомохронности в гидроаэромеханике.
При изучении нек-рых процессов удобно пользоваться также Архимеда числом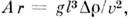 числом Галилея Ga = Re2/ Fr, числом кавитации
числом Галилея Ga = Re2/ Fr, числом кавитации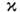 =
2Еи и
др. П. к. В приведённых выражениях
=
2Еи и
др. П. к. В приведённых выражениях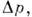
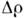 - характерные разности давлений и плотностей, с - скорость звука,
- характерные разности давлений и плотностей, с - скорость звука,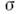 - поверхностное натяжение,
- поверхностное натяжение,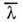 - длина свободного пробега молекул, f - характерная частота.
- длина свободного пробега молекул, f - характерная частота.
П. к., связанные с переносом теплоты: температурный фактор
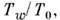 Нусселъта
число
Нусселъта
число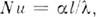 Стентона
число
Стентона
число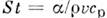 ,
Грасгофа
число
,
Грасгофа
число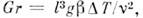 Пепле
число Ре = Re х Pr, Рэлея число Ra = Gr х Pr и
Фурье
число Fo = at/l2, являющееся критерием гомохронности тепловых
процессов. (См. также Био число
Пепле
число Ре = Re х Pr, Рэлея число Ra = Gr х Pr и
Фурье
число Fo = at/l2, являющееся критерием гомохронности тепловых
процессов. (См. также Био число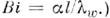 В этих выражениях Тw.,
В этих выражениях Тw.,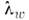 - темп-pa и коэф. теплопроводности стенки, обтекаемой жидкостью или
газом, Т0 - темп-pa торможения потока,
- темп-pa и коэф. теплопроводности стенки, обтекаемой жидкостью или
газом, Т0 - темп-pa торможения потока,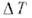 - характерная разность температур,
- характерная разность температур,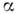 - коэф. теплопередачи.
- коэф. теплопередачи.
Аналогичные П. к. характеризуют перенос материи в бинарной смеси (массопередачу): число Нуссельта для массопередачи
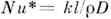 (наз. также диффузионным числом Нуссельта NuD), число
Пекле для массопередачи
(наз. также диффузионным числом Нуссельта NuD), число
Пекле для массопередачи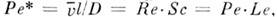 число Стентона
число Стентона
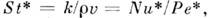 число Грасгофа
число Грасгофа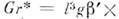
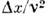 и число Фурье Fo* = Dt/l2 = Fo/Le, являющееся
критерием гомохронности для массопередачи. Здесь k - коэф. массопередачп,
и число Фурье Fo* = Dt/l2 = Fo/Le, являющееся
критерием гомохронности для массопередачи. Здесь k - коэф. массопередачп,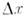 - характерная разность мольных долен вещества в смеси,
- характерная разность мольных долен вещества в смеси,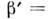
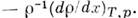 Основными П. к. в магн. гидродинамике являются магн. число Прандтля
Основными П. к. в магн. гидродинамике являются магн. число Прандтля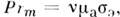 магн. число Рейнольдса
магн. число Рейнольдса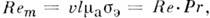 Алъвена
число Аl = v/vА, Гартмана число
Алъвена
число Аl = v/vА, Гартмана число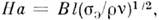 числа
Каулинга Со1 = На2/Re и Со2
= Аl-2 и критерий магнитодинамич. гомохронности
числа
Каулинга Со1 = На2/Re и Со2
= Аl-2 и критерий магнитодинамич. гомохронности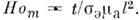 В этих выражениях
В этих выражениях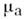 - абс. магн. проницаемость,
- абс. магн. проницаемость,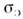 - уд. проводимость, В - плотность магн. потока (магн. индукция),
- уд. проводимость, В - плотность магн. потока (магн. индукция),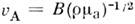 - альвеновская скорость.
- альвеновская скорость.
В электротехнике в случае подобия электрич. цепей с распределёнными параметрами основными П. к. являются L/Rt и C/Gt, где L - индуктивность, R - электрич. сопротивление, С - ёмкость, G - электрич. проводимость.
Построены и используются П. к. для гидродинамики стратифицир. сред (число Ричардсона), газожидкостных (число Марангони) и дисперсных систем, лучистого теплообмена (числа Планка, Бугера, Больцмана) и др. физ. процессов.

