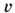частицы жидкости на оси координат представляются в виде частных производныхПотенциальное течение - безвихревое движение жидкости или газа, при к-ром каждый малый объём деформируется и перемещается
поступательно, но не имеет вращения (вихря). При П. т. проекции скорости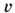
частицы жидкости на оси координат представляются в виде частных производных
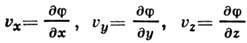
от функции f координат и времени, наз. потенциалом
скорости течения. Движение реальных жидкостей и газов будет потенциальным в
тех областях, в к-рых действие сил вязкости ничтожно мало по сравнению с действием
сил давления (жидкость считается идеальной) и в к-рых нет завихрений, образовавшихся
за счёт срыва со стенок пограничного слоя или за счёт неравномерного нагревания.
Необходимыми и достаточными условиями потенциальности течения являются равенства
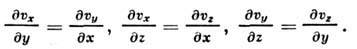
Простейшими примерами П. т. служат поступат.
течение с пост. скоростью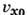 
вдоль
оси x (
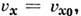
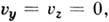потенциал 
''
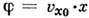+ const), а также источник
и сток в пространстве, для к-рых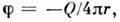 
где Q - постоянная (Q = const) или переменная (Q = Q(t))мощность источника (стока), 
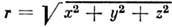- расстояние от начала координат. При Q > 0 жидкость вытекает из начала
координат во всех направлениях (точечный источник), а при Q < 0 -
втекает в начало координат (сток).
Движение идеальной жидкости, возникшее из состояния
покоя, будет потенциальным; будучи потенциальным в к--л. момент времени, оно
будет потенциальным и в последующее время, если давление зависит только от плотности
и массовые силы являются консервативными (см. Консервативная система ).Движение
идеальной несжимаемой (плотность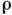 
=
const) жидкости, вызванное мгновенным приложением импульс-них давлений (внезапное
движение погружённого тела, удар тела о
поверхность жидкости), будет также потенциальным.
Для П. т. дифференц. ур-ния движения идеальной
жидкости приводятся к интегралу Лагранжа - Коши:
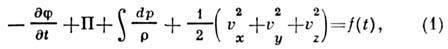
где П - потенц. энергия поля массовых сил,
приходящаяся на единицу массы,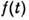 
-
произвольная функция от времени t.
Для установившегося движения соотношение (1)
принимает вид
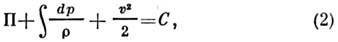
где С - постоянная для всей области П.
т. сжимаемой жидкости. Т. о., для изучения П. т. достаточно определить потенциал
скоростей с помощью неразрывности уравнения, соотношения (2) и ур-ния
физ. состояния. Для несжимаемой жидкости ур-ние неразрывности имеет вид
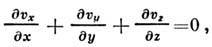
и поэтому изучение П. т. сводится к, решению
ур-ния Лапласа
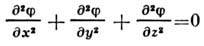
с учётом граничных условий на твёрдых стенках
и на свободной поверхности (условий безотрывности обтекания твёрдых стенок и
условия постоянства давления на свободной поверхности).
Для плоскопараллельного П. т. несжимаемой жидкости
ур-ние неразрывности позволяет ввести функцию тока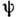
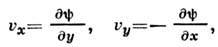
к-рая в комбинации с потенциалом скоростей f
составляет комплексный потенциал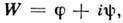 
представляющий функцию от комплексного переменного
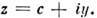С помощью комплексного потенциала скоростей изучаются безотрывное обтекание
плоского контура, струйное обтекание стенок и волновое движение. Безотрывное
П. т. вокруг плоского контура может быть бесциркуляционным или циркуляционным.
В первом случае результирующее воздействие жидкости на плоский контур равно
нулю (см. Д-Аламбера - Эйлера парадокс), во втором - результирующее
воздействие потока жидкости на контур сводится к подъёмной силе, а в
случае струйного П. т. вокруг плоского контура - к силе сопротивления, пропорциональной
квадрату скорости. П. т. имеет место также при движениях сжимаемой жидкости
или газа, представляющих собой малые возмущения нек-рого известного состояния
равновесия пли движения, напр. при распространении звука в среде; при этом малый
избыток давления над давлением в состоянии равновесия среды связан с потенциалом
скоростей соотношением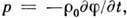 
а из ур-ния неразрывности в случае, когда потенциал массовых сил не зависит
от времени, получается волновое ур-ние
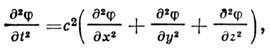
где с - скорость распространения звука,
вычисленная для невозмущённого состояния покоя: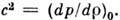
Для П. т. газа при адиабатич. законе дифференц. ур-ние для потенциала скоростей
становится нелинейным, но с помощью преобразования С. А. Чаплыгина оно приводится
к линейному ур-нию, разрешаемому в ряде случаев.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
