Стокса теорема. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Стокса теорема - обобщение Стокса формулы, утверждение о равенстве интеграла от внеш. дифференциала dw дифференциальной формы по ориентированному компактному многообразию М интегралу от самой формы по ориентированному (согласованно с ориентацией многообразия М)краю дМ многообразия М:

Широко известными частными случаями ( * ) являются Гаусса - Остроградского формула, Грина формулы. СТОКСА ФОРМУЛА - одна из осн. интегральных теорем векторного анализа, связывающая поверхностный интеграл с криволинейным:

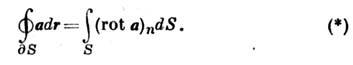
Здесь dS - замкнутая кривая, ограничивающая поверхность S, (rot a)_n- проекция на внеш. нормаль к поверхности. Согласно С. ф., циркуляция векторного поля а вдоль любой замкнутой кривой (левая часть равенства) равна потоку поля rota через поверхность, опирающуюся на эту кривую. Из С. ф. следует, что циркуляция безвихревого поля (т. е. такого, что rot a = 0) вдоль любой замкнутой кривой равна 0. С. ф. и Гаусса - Остроградского формула являются частными случаями Стокса теоремы, к-рая связывает между собой интегралы от внешних дифференциальных форм разных размерностей.

Знаете ли Вы, как разрешается парадокс Ольберса?
(Фотометрический парадокс, парадокс Ольберса - это один из парадоксов космологии, заключающийся в том, что во Вселенной, равномерно заполненной звёздами, яркость неба (в том числе ночного) должна быть примерно равна яркости солнечного диска. Это должно иметь место потому, что по любому направлению неба луч зрения рано или поздно упрется в поверхность звезды.
Иными словами парадос Ольберса заключается в том, что если Вселенная бесконечна, то черного неба мы не увидим, так как излучение дальних звезд будет суммироваться с излучением ближних, и небо должно иметь среднюю температуру фотосфер звезд. При поглощении света межзвездным веществом, оно будет разогреваться до температуры звездных фотосфер и излучать также ярко, как звезды. Однако в дело вступает явление "усталости света", открытое Эдвином Хабблом, который показал, что чем дальше от нас расположена галактика, тем больше становится красным свет ее излучения, то есть фотоны как бы "устают", отдают свою энергию межзвездной среде. На очень больших расстояниях галактики видны только в радиодиапазоне, так как их свет вовсе потерял энергию идя через бескрайние просторы Вселенной. Подробнее читайте в FAQ по эфирной физике.