Трмодинамика низкотемпературной плазмы. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Трмодинамика низкотемпературной плазмы

Трмодинамика низкотемпературной плазмы - раздел физики плазмы, изучающий общие свойства макроскопич. плазменных систем, находящихся в состоянии термодинамич. равновесия. Обычно равновесное состояние системы при разных значениях параметров (давление р, темп-pa Т)изображается на фазовой диаграмме р-Т. Плазменные состояния вещества занимают осн. часть фазовой диаграммы и чрезвычайно многообразны (см. рис. к ст. Неидеальная плазма ).Термодинамика плазмы проста лишь на периферии этой диаграммы - при экстремально высоких плотностях и при высоких темп-pax. В обоих предельных случаях - это системы идеальных газов - электронов и ионов, но в первом случае вырожденных, а во втором - классических. К этим областям прилегают области слабой неидеальности, в к-рых методами теории возмущений найдены поправки на слабые межчастичные взаимодействия. В значит. части фазовой диаграммы плазма неидеальна, и последоват. теоретич. описание возможно, если осуществима перенормировка взаимодействия, как, напр., в случае образования связанных электронно-ионных пар, т. е. атомов в низкотемпературной плазме (НП) или в случае образования ионной решётки. В областях сильной неидеальности теоретич. модели опираются на результаты измерений. Экспериментально наиб. изучена частично ионизованная плазма, используемая во мн. приложениях. Модельная однокомпо-нентная плазма детально исследована теоретически.

Однокомпонентная плазма. Модель классич. однокомпонентной плазмы представляет собой плазму точечных ионов с зарядом Ze, помещённых в равномерно распределённую среду электронов. Состояние плазмы характеризуется единственным параметром - параметром неидеальности g= (Ze)²/r_ikT, где r_i= [3/(4pn_i)]^1/3-ср. расстояние между ионами. Плазма неидеальна, если g>1. Такова плазма недр звёзд белых карликов и планет-гигантов Солнечной системы, где величины g имеют порядок 100 или 10, а электронный газ у них вырожден и идеален.

Термодинамика однокомпонентной плазмы проста в предельных случаях. Если g << 1 (малые плотности, высокие температуры-идеальная плазма), плазма газообразна, она описывается дебаевским приближением. На расстоянии дебаевского радиуса экранирования r_D = (4pn_iZ²e²/kT)^-1/2осуществляется экранировка заряда, а поправка к внутр. энергии идеального газа равна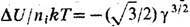

В пределе сильной неидеальности, когда g >>1, сильное кулоновское отталкивание локализует ионы в пространственную структуру (кулоновский кристалл), внутр. энергия к-рой близка к U/п_ikТ= -0,9g. Примерами такой неидеальной плазмы является кристаллизованная одно-компонентная плазма примеси многозарядных (Z >> 1) ионов в недрах тяжёлых планет и двумерная одноком-понентная плазма электронов на поверхности жидкого гелия.

Область промежуточных g исследована методами машинного эксперимента. По мере роста g нарастают межионные корреляции, что ясно отражается на виде бинарной корреляц. функции ионов g(r)(рис. 1) [1 ]. Расчёты показывают, что кулоновский кристалл плавится при g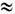170.

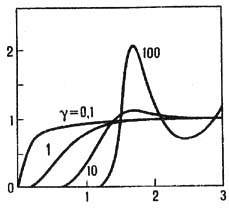
Рис. 1. Расчётные бинарные корреляционные функции ионов g(r/r_i) при различных параметрах неидеальности однокомпонентной плазмы (по горизонтальной оси r/r_i).

Вырожденной однокомпонентной плазмой является при низких темп-pax электронная плазма на положительно заряженном фоне. Её состояние характеризует величина ср. межэлектронного расстояния r_s, выраженного в радиусах Бора a₀: r_s= [3/{4pn_e)]^1/3/a₀. Через r_s выражается параметр неидеальности вырожденной электронной плазмы g_в= 0,543 r_s (см. Неидеальная плазма). К вырожденной однокомпонентной плазме близка плазма валентных электронов в металлах, для к-рых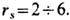

При T=0 электроны в сильно сжатой плазме, когда r_s<< l, представляют собой слабо неидеальный газ. Энергия основного состояния в расчёте на. один электрон, выраженная в Ry (ридберг равен энергии ионизации атома водорода), имеет вид:

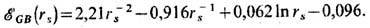
Сюда дают вклады кинетич. энергия, обменная энергия (см. Обменное взаимодействие)и вычисленная М. Гелл-Маном и К. Бракнером (М. Gell-Mann, К. Brueckner, 1957) корреляционная энергия. В противоположном пределе r_s>> 1, когда электроны находятся в поле положительного равномерно распределённого заряда при низких температурах и на расстояниях значительно больших Бора радиуса ,электроны настолько коррелированы, что образуют вигнеров-ский кристалл. В этих условиях энергия основного состояния имеет вид:

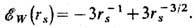
Принято считать, что вигнеровский кристалл плавится при r_s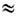20. Однако эта цифра требует уточнения.

Точное выражение для корреляц. энергии при промежуточных r_s отсутствует. Имеется целый набор интер-поляц. ф-л для корреляц. энергии, начиная с простейшей, предложенной Е. Вигнером (Е. Wigner, 1934): 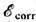= -0,88(r_s + 7,8)^-1. Величина 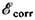через структурный фактор S(q)однокомпонентной плазмы связана с её ди-электрич. проницаемостью e(q, w) и может быть вычислена, если последняя известна.

Частично ионизованная невырожденная плазма. Если энергия ионизации атома I значительно превосходит температуру, электронно-ионное взаимодействие приводит к образованию связанных электронно-ионных состояний - атомов. Это имеет место, если выполняется неравенство Ry/kT >>1. Т.к. появляются атомы, плазма становится трёхкомпонентной. Она оказывается также классической, поскольку расстояние макс. сближения электронов e²/kT>>l_e (l_e-тепловая длина волны электрона). Трёх-компонентная, иначе говоря, частично ионизованная, плазма существует в области I (см. рис. к ст. Неидеальная плазма ).Она является невырожденной. Слабое взаимодействие между оставшимися свободными электронами и ионами вычисляется в рамках теории возмущений. Частично ионизованная плазма возникает в многочисл. газоразрядных техн. устройствах.

Концентрации свободных электронов, атомов и ионов связаны ур-нием Саха:

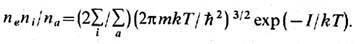
Здесь -внутр. статистич. суммы иона и атома.

Вследствие 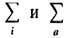дальнодействия кулоновских сил статистич. сумма уединённого атома есть расходящийся ряд. Напр., для атома водорода

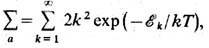
где 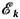= Ry/k²; расходится и второй вириальный коэф., т. к. расходятся интегралы 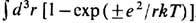, но эти расходимости взаимно сокращаются. Корректный учёт взаимодействия исходных электронов и ионов приводит к перенормировке статистич. суммы

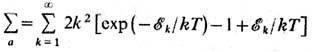
и к уменьшению энергии ионизации на величину DI=e²/r_D, где радиус экранирования

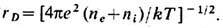
Такая плазма представляет собой смесь идеальных газов электронов, атомов и ионов. Поправка к свободной энергии идеальной классич. плазмы обусловлена корреляцией заряж. частиц

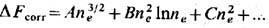
Первый член описывает длинноволновые дебаевские корреляции DF_D= - Т/12pr³_D ; его учёт приводит к ур-нию состояния в виде Дальтона закона (давление идеальных газов равно сумме парциальных давлений) с малой поправкой: р= Тп_а + 2Тп_е(1 - e²/3r_DT). Второй член в плазме с однократной ионизацией исчезает.

Неидеальная классическая плазма. На рис. 2 изображена расчётная зависимость степени ионизации х = п_е/(п_i + п_а)водородной плазмы от плотности и температуры [4]. При малых плотностях ионизация является термической: х уменьшается при сжатии (сплошные кривые слева) и возрастает при нагреве в соответствии с ур-нием Саха. Степень неидеальности характеризуется параметром g = e²/kTr_i. Измерения ур-ния состояния цезиевых паров, сжатых в подогреваемых ударных трубах, показали, что вплоть до значений g, близких к единице, термодинамика неидеальной классич. плазмы близка к термодинамике идеальной плазмы.

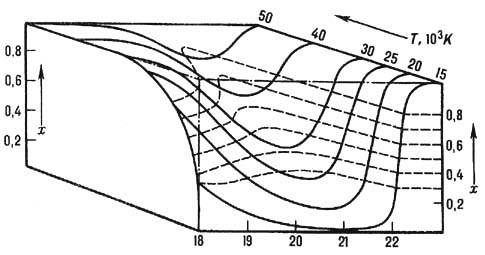
Рис. 2. Зависимость степени ионизации x водородной плазмы от плотности (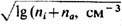 ) и температуры ( штриховые кривые).

При высоких плотностях рост степени ионизации вызван сжатием вещества. Это область сильно неидеальной плазмы. Соответствующие ей участки кривых (сплошные в правой части рис. 2) являются ориентировочными. Энергетич. спектр атомов деформируется, поскольку поля ионов экранируются на малых расстояниях. Постепенно радиусом экранирования становится не дебаевский, а среднее межчастичное расстояние r_i.

По мере дальнейшего сжатия исчезают возбуждённые состояния, соответственно понижается граница континуума. Когда радиус экранирования оказывается близким к размеру атома в основном состоянии а₀, энергетич. щель в спектре закрывается и атомы исчезают. Это условие наз. критерием Мотта для перехода вещества в металлич. состояние (см. Моттовские диэлектрики ).Измерения электропроводности, выполненные при изобарич. нагреве жидких металлов в омических печах, показали, что переход из металлич. состояния в пары металлов (переход Мотта) является не скачкообразным, а довольно плавным (см. Переход металл - диэлектрик).

Эксперименты указывают на высокие значения концентраций заряж. частиц в окрестности критич. точек ряда металлов. Возможно, что за конденсацию вещества в этой области ответственно сильное кулоновское взаимодействие.

Вырожденная плазма сильно сжатого вещества. При сильном сжатии электронная компонента вырождается и становится тем более идеальна, чем выше плотность. Все электроны в результате сжатия вещества и смятия электронных оболочек оторваны от ядер и образуют однородный электронный газ. Если ср. расстояние r_ср между частицами этого газа меньше радиуса оболочки r_cp<a₀/Z, то параметр неидеальности по взаимодействию электронов с ядрами имеет вид:

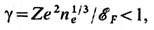
где 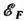-энергия Ферми. Система положительно заряженных ядер, ещё очень далёкая от вырождения, сильно неидеальна и образует упорядоченную решётку. Соответственно этому давление даётся выражением

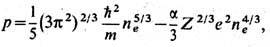
где a - т. н. постоянная Маделунга, зависящая от конкретной структуры решётки. Так, напр., для вигнеровских ячеек (см. Вигнеровский кристалл)a =0,9(4p/3)^1/3. Плазма сильно сжатого вещества (т. е. при высоких давлениях) может считаться холодной вплоть до чрезвычайно высоких температур (см. рис. 1,2 к ст. Низкотемпературная плазма). Т. о., при экстремально высоких давлениях свойства веществ универсализуются - ат. номер входит в виде комбинаций pZ^-10/3, n_eZ^-2, TZ^-4/3. Такие условия реализуются, напр., в недрах звёзд.

С уменьшением плотности возникают новые эффекты. При не очень высоких темп-pax основными из них являются обменные и квантовые, к-рые в случае слабой неоднородности дают поправку к давлению

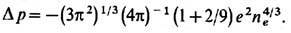
Диапазон плотностей, в к-ром выполняются неравенства a₀^-3<< n_e<<Z²a₀^-3, достаточно широк для плазмы тяжёлых элементов (Z>>l). На своей ниж. границе он соответствует давлению р= е²a₀^-4 = 300 Мбар. Давления, близкие к 100 Мбар, зафиксированы экспериментально за ударными волнами, порождаемыми мощными взрывами. В этих условиях пространственное распределение электронов становится неоднородным, поскольку они притягиваются к ядрам. Существенно, что каждое ядро экранируется своими Z электронами, и плазма разбивается на совокупность независимых ячеек.

В таком ячеечном приближении слабонеоднородная плазма описывается Томаса - Ферми методом. Ур-ние Томаса- Ферми, решаемое в конечном объёме ячейки (4p/3)r_i³, описывает атом в сжатом состоянии. При этом сохраняется автомодельность по Z. В области низких давлений метод Томаса - Ферми, даже с учётом обменных, квантовых и корреляц. эффектов, даёт только качеств. описание усреднённых характеристик, к-рые измеряются при изоэнтропич. расширении конденсированного вещества, предварительно сжатого и разогретого во фронте ударной волны. На рис. 3 представлена изобара объёма u, приходящегося на один атом вещества [5]. Кривая, проведённая по эксперим. точкам, отражает осцилляции, вызванные обо-лочечными эффектами, обусловленными дискретным спектром энергии. Кривая, рассчитанная методом Томаса- Ферми (МТФ), передаёт усреднённый ход u(Z),

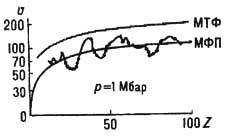
Рис. 3. Зависимости изобары объёма и, приходящегося на один атом вещества, от величины заряда Z; МТF - расчёт методом Томаса - Ферми; МФП - расчёт методом функционала плотности; осциллирующая кривая-экспериментальная.

На рис, 3 представлена также зависимость u(Z), полученная с помощью одного из простейших вариантов метода функционала плотности (МФП) термодинамич, потенциала. Этот метод наиб. перспективен; он позволяет описать термодинамику сжатой плазмы в широком диапазоне параметров.

Литература по

Ichimaru S., Strongly coupled plasmas: high-density classical plasmas and degenerate electron liquids, "Revs Mod. Phys,", 1982, v, 54, № 4, p. 1017; 2) Фортов В. Е,, Якубов И. Т., Неидеальная плазма, М,, 1994; 3) Веденов А. А., Термодинамика плазмы, в сб.: Вопросы теории плазмы, под ред. М. А. Леонтовича, в. 1, М., 1963, с. 273; 4) Крефт В--Д., Кремп Д., Эбелинг В., Рёпке Г., Квантовая статистика систем заряженных частиц, пер. с англ., М., 1988; 5) Киржниц Д. А., Лозовик Ю. Е., Шпата-ковская Г. В., Статистическая модель вещества, "УФН", 1975, т. 117, с, 3. И. Т. Якубов.

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что, как и всякая идолопоклонническая религия, релятивизм представляет собой инструмент идеологического подчинения одних людей другим с помощью абсолютно бессовестной манипуляции их психикой для достижения интересов определенных групп людей, стоящих у руля этой воровской машины? Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира