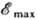 от интенсивности света, линейную зависимость
от интенсивности света, линейную зависимость 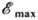 от его частоты со и существование граничной (мин.) частоты w0 (пороговой
энергии
от его частоты со и существование граничной (мин.) частоты w0 (пороговой
энергии 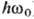 ) Фотоэффекта.
) Фотоэффекта.Фотоэффект - испускание электронов веществом при поглощении им квантов эл--магн. излучения
(фотонов). Ф. был открыт Г. Герцем (G. Hertz) (1887), к-рый установил, что длина
искры в разряднике увеличивается при попадании на его металлич. электроды света
от искры др. разрядника. Первые исследования Ф. выполнены А. Г. Столетовым (1888).
Ф. Ленард (Ph. Lenard) и Дж. Дж. Томсон (J. J. Thomson) (1889) доказали, что
при Ф. испускаются электроны. Открытие и исследование Ф. сыграло важную роль
в эксперим. обосновании квантовой теории. Только на основе гипотезы о квантовании
энергии эл--магн. поля, проявляющемся в процессах испускания и поглощения света,
удалось объяснить осн. закономерности Ф.: независимость макс. кинетич. энергии фотоэлектронов 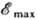 от интенсивности света, линейную зависимость
от интенсивности света, линейную зависимость 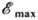 от его частоты со и существование граничной (мин.) частоты w0 (пороговой
энергии
от его частоты со и существование граничной (мин.) частоты w0 (пороговой
энергии 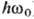 ) Фотоэффекта.
) Фотоэффекта.
Свободный электрон не может поглотить фотон, т. к. при этом не могут быть одновременно соблюдены законы
сохранения энергии 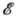 и импульса р. Это видно уже из того, что для оптич. перехода свободного
электрона из состояния
и импульса р. Это видно уже из того, что для оптич. перехода свободного
электрона из состояния 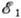 ,
p1 в состояние
,
p1 в состояние 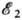 ,
р2 в отсутствие 3-го тела (конденсир. среды, атома
или рассеянного фотона) законы сохранения энергии и импульса
,
р2 в отсутствие 3-го тела (конденсир. среды, атома
или рассеянного фотона) законы сохранения энергии и импульса 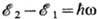 , p2- p1=
, p2- p1=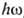 /c несовместимы ни при какой скорости электрона u<c. В конденсир.
среде связь электрона с окружением характеризуется работой выхода Ф.
Кинетич. энергия фотоэлектрона
/c несовместимы ни при какой скорости электрона u<c. В конденсир.
среде связь электрона с окружением характеризуется работой выхода Ф.
Кинетич. энергия фотоэлектрона 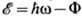 .
При температуре T=0 К и не очень высокой интенсивности света, когда многофотонные
процессы практически отсутствуют, Ф. возникает только при
.
При температуре T=0 К и не очень высокой интенсивности света, когда многофотонные
процессы практически отсутствуют, Ф. возникает только при 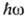 >=Ф.
По установившейся терминологии, Ф. в конденсир. среде наз. фотоэлектронной
эмиссией, а переход электрона из одного из связанных состояний в атоме или
молекуле в непрерывный спектр наз. фотоионизацией (см. Ионизация ).Для
водородоподобного атома необходимая для фотоионизации энергия фотона равна
>=Ф.
По установившейся терминологии, Ф. в конденсир. среде наз. фотоэлектронной
эмиссией, а переход электрона из одного из связанных состояний в атоме или
молекуле в непрерывный спектр наз. фотоионизацией (см. Ионизация ).Для
водородоподобного атома необходимая для фотоионизации энергия фотона равна
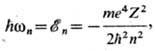
где Z-заряд ядра
в единицах заряда электрона, n - гл. квантовое число связанного состояния.
Энергия, необходимая для перевода электрона из осн. состояния в атоме (n=1)
в состояние непрерывного спектра с нулевой кинетич. энергией, наз. энергией
ионизации атома, а если она измеряется в эВ-потенциалом ионизации I.
В водородоподобном
атоме 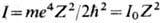 ,
где I0 - энергия ионизации атома водорода. В многоэлектронных
атомах фотоны достаточно большой энергии могут выбивать электроны из разных
электронных оболочек. Такие атомы имеют неск. потенциалов ионизации.
,
где I0 - энергия ионизации атома водорода. В многоэлектронных
атомах фотоны достаточно большой энергии могут выбивать электроны из разных
электронных оболочек. Такие атомы имеют неск. потенциалов ионизации.
Др. характеристика Ф.-
сечение фотоионизации а. Оно равно отношению числа актов ионизации, приходящихся
на один атом в единицу времени в единице объёма, к интенсивности потока фотонов
(монохроматических). Величина а может быть вычислена аналитически для атома
водорода и для водородоподобного иона с зарядом ядра Z<<137. В нерелятивистском
случае (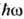 <<тс2)дифференц. сечение фотоионизации с испусканием электрона в элемент телесного
угла do
<<тс2)дифференц. сечение фотоионизации с испусканием электрона в элемент телесного
угла do
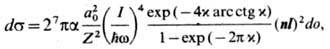
где a = е2/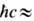 1/137
- постоянная тонкой структуры, a0 = =
1/137
- постоянная тонкой структуры, a0 = =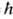 2/те2,
2/те2, 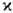 =Ze2/
=Ze2/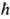 u,
n - единичный вектор направления вылета электронов, l-единичный
вектор поляризации фотонов. Величина (nl)2 определяет
угл. распределение фотоэлектронов. В полярных координатах с осью oz вдоль
направления распространения света угл. распределение фотоэлектронов имеет вид
u,
n - единичный вектор направления вылета электронов, l-единичный
вектор поляризации фотонов. Величина (nl)2 определяет
угл. распределение фотоэлектронов. В полярных координатах с осью oz вдоль
направления распространения света угл. распределение фотоэлектронов имеет вид
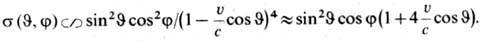
При малых скоростях электронов
(u<<c)они вылетают в осн. в направлении электрич. вектора
световой волны.
При неполяризованном свете
максимум распределения лежит в экваториальной плоскости J= p/2. С увеличением
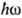 и соответственно
u максимум смещается в направлении распространения света на величину
угла Jmax
и соответственно
u максимум смещается в направлении распространения света на величину
угла Jmax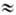 p/2
- 4u/c (рис. 1). Полное сечение Ф. для перехода из основного 1s-состояния
(см. Атом)
p/2
- 4u/c (рис. 1). Полное сечение Ф. для перехода из основного 1s-состояния
(см. Атом)
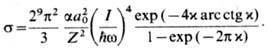
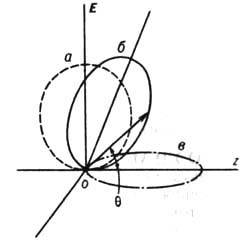
Рис. 1. Угловое распределение
фотоэлектронов. Полярная диаграмма в плоскости j= 0. Ось oz - направление
распространения излучения, ось оЕ-направление электрического вектора
световой волны; а -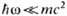 , в-
, в-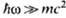 б-
б-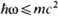 .
.
Видно, что непосредственно
у порога Ф. сечение а стремится к постоянной величине. Предельное значение а
при 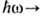 I
(
I
(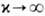 ) равно
) равно
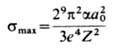
(здесь е = 2,718...).
При небольшом превышении
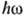 над I,
когда ещё
над I,
когда ещё 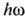 -I<<I (
-I<<I (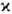 >>1),
s~(I/
>>1),
s~(I/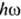 )8/3.
При
)8/3.
При 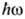 -I
-I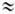 I
(
I
(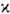 ~1) s~(I/
~1) s~(I/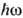 )3,
а вдали от границы поглощения при
)3,
а вдали от границы поглощения при 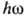 >>I
(
>>I
(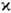 <<1,
но ещё
<<1,
но ещё 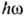 <<mс2)
s~(I/
<<mс2)
s~(I/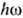 )7/2.
В табл. приведены потенциалы ионизации и сечения фотоэффекта нек-рых атомов
и молекул, а на рис. 2 - зависимости а(
)7/2.
В табл. приведены потенциалы ионизации и сечения фотоэффекта нек-рых атомов
и молекул, а на рис. 2 - зависимости а(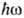 /I)
для атомов Н, Не и иона Н-.
/I)
для атомов Н, Не и иона Н-.
Для нерелятивистских скоростей
фотоэлектронов получены точные ф-лы для а возбуждённых атомов (переходы из состояний
с n>1). В приближённых расчётах для n>=1 и 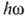 <=I
часто пользуются квазиклассической Крамерса ф-лой:
<=I
часто пользуются квазиклассической Крамерса ф-лой:
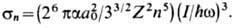
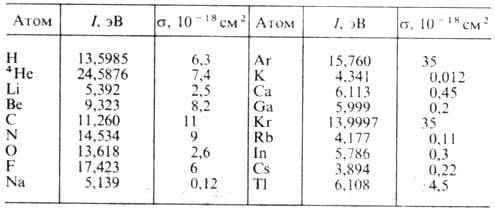
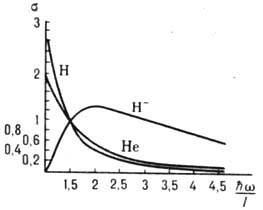
Рис. 2. Зависимость
сечения фотоэффекта а из основных состояний атомов Н, Не и иона Н- от
энергии фотонов. Масштабы кривых (в относительных единицах) выбраны так, чтобы
s=1 при 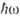 /I=1,5.
/I=1,5.
В многоэлектронных атомах
со средними и большими Z в рентг. и у-излучении Ф. происходит на электронах
внутр. оболочек, в осн. на К-электронах. При увеличении (2p/h)w
и достижении значения 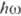 =
IK s скачкообразно увеличивается. При дальнейшем возрастании
энергии фотонов в конкуренцию с Ф. вступает рассеяние фотона на электроне (Комптона
эффект), а в релятивистском случае, когда
=
IK s скачкообразно увеличивается. При дальнейшем возрастании
энергии фотонов в конкуренцию с Ф. вступает рассеяние фотона на электроне (Комптона
эффект), а в релятивистском случае, когда 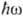 /2тс2>=1-рождение электрон-позитронных
пар. На рис. 3 приведены зависимости сечений трёх процессов от энергии фотонов
при прохождении излучения через молибден (Z = 42), к-рые дают представление
об их соотношении. При очень больших энергиях фотонов (
/2тс2>=1-рождение электрон-позитронных
пар. На рис. 3 приведены зависимости сечений трёх процессов от энергии фотонов
при прохождении излучения через молибден (Z = 42), к-рые дают представление
об их соотношении. При очень больших энергиях фотонов (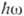 >>mс2,
ультрарелятивистский случай) сечение Ф. равно
>>mс2,
ультрарелятивистский случай) сечение Ф. равно
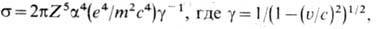
фотоэлектроны испускаются в осн. в малый телесный угол в направлении распространения излучения.
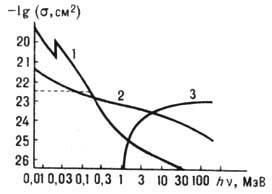
Рис. 3. Сечения фотоэффекта
(1), рассеяния фотонов (2) и
рождения пар (3) в молибдене (Z = 42).
Механизм Ф. на валентных
электронах водородоподоб-ных примесных атомов в полупроводниках при 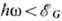 (
(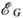 -ширина
запрещённой зоны полупроводника) подобен описанному с той разницей, что атом
находится в кристалле и в него же испускаются фотоэлектроны. Вследствие этого
в соответствующих выражениях фигурируют диэлектрич. проницаемость кристалла
и эфф. масса электрона. В водородоподобных примесях нек-рых полупроводников
а может достигать ~ 10-15 см2.
-ширина
запрещённой зоны полупроводника) подобен описанному с той разницей, что атом
находится в кристалле и в него же испускаются фотоэлектроны. Вследствие этого
в соответствующих выражениях фигурируют диэлектрич. проницаемость кристалла
и эфф. масса электрона. В водородоподобных примесях нек-рых полупроводников
а может достигать ~ 10-15 см2.

Бете Г., Солпитер Э., Квантовая механика атомов с одним и двумя электронами, пер. с англ., М., 1960, с. 464-503;
Бете Г., Квантовая механика, пер. с англ., М., 1965, с. 205-10;
Собельман И. И., Введение в теорию атомных спектров, 2 изд., М., 1977, с. 248-55; с. 261-68;
Физические величины. Справочник, под ред. И. С. Григорьева, Е. 3. Мейлихова, М., 1991, с. 409-12.
Т. М. Лифшиц.
|
|