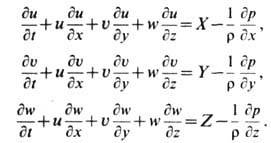
Эйлера уравнение в гидромеханике - дифференц. ур-ние движения идеальной жидкости в переменных Эйлера. Если давление р, плотность р, проекции скоростей частиц жидкости и, v, w к проекции
действующей объёмной силы X, Y, Z рассматривать как функции координат х,
у, z точек пространства и времени t (переменные Эйлера), то
Э. у. в проекциях на оси прямоуг. декартовой системы координат принимает вид
системы ур-ний:
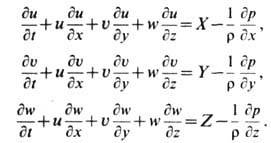
Решение общей задачи гидромеханики в переменных
Эйлера сводится к тому, чтобы, зная X, Y, Z, а также начальные и граничные
условия, определить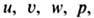
р как функции х, у, z и t. Для этого к Э. у. присоединяют ур-ние
неразрывности в переменных Эйлера:
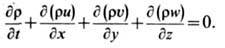
В случае баротропной жидкости, у к-рой плотность
зависит только от давления, 5-м ур-нием будет ур-ние состояния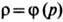
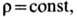(иликогда
жидкость несжимаема).
Э. у. пользуются при решении разнообразных
задач гидромеханики.
Литература по
Лойцянский Л. Г., Механика жидкости
и газа, 6 изд., М„ 1987. С.
M. Торг.
Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.
р как функции х, у, z и t. Для этого к Э. у. присоединяют ур-ние
неразрывности в переменных Эйлера:
(или
когда
жидкость несжимаема).
