Электронные линзы - устройства, создающие магн. или электрич. поля для фокусировки электронных
пучков, их формирования и получения электронно-оптич. изображений (аналогичные
устройства для ионных пучков наз. ионными линзами). Их классифицируют по типу
поля (магнитные, электростатические), по виду симметрии (осе-симметричные, цилиндрические,
квадрупольные и др.) и по др. характерным признакам.
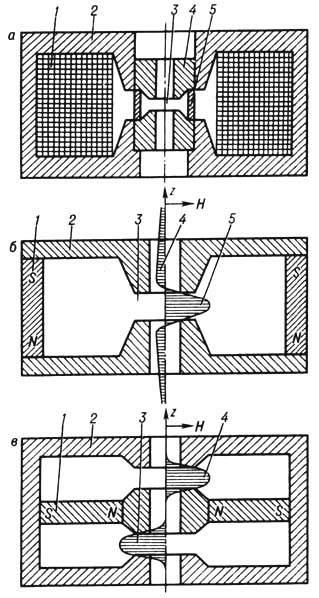
Магнитные электронные линзы. по способу возбуждения магн. поля делятся на электромагнитные и магнитостатические. Эл--магн. панцирная (бронированная) линза (рис. 1,a) состоит из обмотки 1, по к-рой протекает ток, возбуждающий фокусирующее магн. поле в межполюсном зазоре 3 (щели) линзы, магнитопровода 2, окружающего обмотку (создаёт панцирь, откуда и название), и полюсного наконечника 4. Последний изготовляется из магнитомягких сплавов с большой индукцией насыщения и применяется в линзах с большой оптической силой (малым фокусным расстоянием). Фокусировка пучка производится регулированием тока возбуждения, стабильность к-рого должна быть на уровне, обеспечивающем низкие хроматич. аберрации.
Рис. 1. Магнитные электронные
линзы: а-электромагнитная электронная линза: 1-обмотка возбуждения;
2-магнитопровод; 3-межполюсный зазор; 4-полюсный наконечник;
5 -немагнитная вставка, соединяющая полюсы наконечника; б-магнитостатическая
электронная линза: 1 -постоянный магнит; 2 - магнитопровод; 3-межполюсный
зазор; 4-кривая
распределения напряжённости поля рассеяния на оси вне линзы; 5-кривая
распределения напряжённости
поля в линзе; в - блок из двух магнитостатических
линз: 1 - постоянный магнит; 2-магнитопровод;
3,4-кривые распределения поля в линзах.
Проблема стабильности фокусирующего
поля не возникает в магнитостатич. линзе, поле к-рой создаётся с помощью пост.
магнитов. Однако в линзе с одним фокусирующим полем (рис. 1,б) образуются
большие поля рассеяния вокруг её корпуса, а также на оптич. оси вне щели.
Наличие полей на оси следует
из закона полного тока
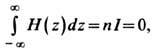к-рый приводит к равенству:
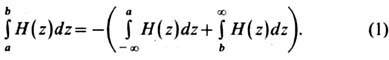
Здесь H(Z)- напряжённость
магн. поля на оптич. оси z, nI-ампервитки, равные нулю в магнитостатич.
Э.л., а и b-границы поля линзы. В левой части (I)стоит
магнитодвижущая сила (МДС) фокусирующего поля, а в правой - МДС полей рассеяния
на оси z вне линзы. Знак минус перед правой частью означает, что направления
магн. полей рассеяния и полей линзы противоположны. Из равенства МДС по абс.
величине следует, что поля рассеяния очень большие, а это ухудшает электрооптич.
параметры линзы и вредно влияет на соседние с ней элементы оптич. системы.
В конструкции, состоящей
из двух магнитостатич. линз (рис. 1, в), магн. поток полностью замкнут
и противоположно направленные поля существуют только в межполюсных зазорах двух
линз. Преимущество магнитостатич. линз - стабильность фокусирующего поля; недостатки
- относительно низкая индукция поля и сложность регулирования их оптич. силы.
Магн. линза считается слабой
(тонкой в световой оптике), если её фокусное расстояние f многократно
превышает протяжённость фокусирующего поля вдоль оси. В этом случае оптич. силу
можно вычислить по ф-ле:
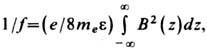
где е, те,
e - заряд, масса и энергия электронов соответственно, B(z) - осевое
распределение индукции магн. поля. Предмет и изображение в слабой линзе расположены
вне поля, и её кардинальные элементы определяются так же, как в световой оптике
(рис. 2, а). Для определения фокальных точек и главных плоскостей достаточно
знать две траектории (т.е. 2 линейно независимых решения ур-ний (9) в ст. Электронная
и ионная оптика). Эти траектории (главные лучи) входят в поле Э.л. параллельно
оптич. оси-одна из пространства предметов, а другая и из пространства изображений
- и пересекают ось z в точках фокусов F0 и Fi. Касательные к лучам в точках фокусов и продолжения параллельных оси участков
этих же лучей, пересекаясь, определяют координаты главных плоскостей Hi и H0. (В отличие от световой оптики, главные плоскости
Э.л. расположены на оси в обратной последовательности.) Известное положение
фокусов и главных плоскостей позволяет построить изображение. Построение изображения
В предмета А проводится по методу Листинга с помощью двух главных
лучей, состоящих из отрезков прямых, к-рые не везде совпадают с реальными лучами
(рис. 2, а). Оба выходят из точки предмета А -один параллельно
оси z (1), другой (2) - через точку фокуса F0· Луч
1 преломляется в главной плоскости Hi и далее идёт
через фокус Fi; луч 2 проходит через фокус F0,
преломляется плоскостью H0 и далее идёт параллельно оси z.
Точка их пересечения
в пространстве изображений дает сопряжённую точку В. Как и в световых
линзах, для тонких линз выполняется ур-ние Ньютона Z0Zi=f0fi,
где Z0 и Zi - расстояния от предмета и от
изображения до соответствующих точек фокусов; f0 и fi
- фокусные расстояния в пространстве предметов и изображений соответственно.
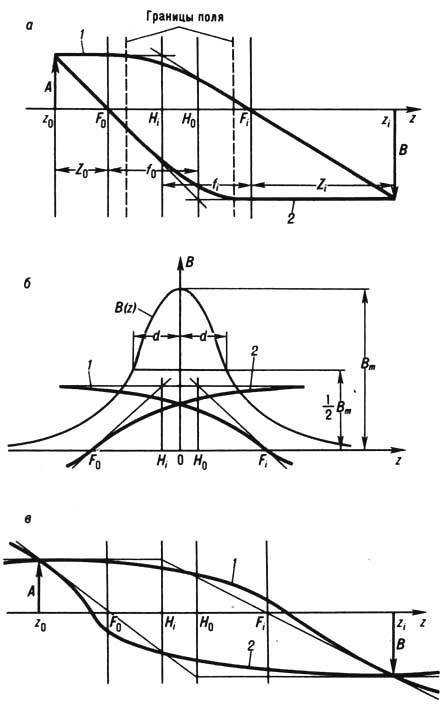
Рис. 2. Построение изображения
В предмета А в фокусирующих полях электронных линз при помощи
главных лучей 1 и 2 и кардинальных элементов- фокальных F0,
Fi и главных H0, Hi плоскостей:
а - предмет и изображение находятся вне поля линзы и выполняется
условие Z0Zi=f0fi;
б-предмет и изображение находятся в колоколообразном поле B(z)=Bm(1+(z/a)2)-1,
Вт-максимальная индукция поля, d-полуширина
кривой распределения поля; в-предмет и изображение находятся в поле любой
формы.
Аберрации магн. линзы зависят
от её МДС и положения плоскости предметов относительно фокусирующего поля. В
частности, сферическая и хроматическая аберрации уменьшаются, если МДС увеличивать
и эту плоскость приближать к центру линзы, где индукция поля максимальна. Поэтому
в целях уменьшения аберраций в электронной оптике чаще используют линзы с большой
МДС, в к-рых предмет и изображение расположены в поле линзы.
Кривая распределения индукции
поля В (z) на оси z магн. линз имеет колоколообразную форму (рис. 2,б), причём наибольшая крутизна падения индукции поля по обе стороны от максимума
наблюдается у линз, у к-рых отсутствует насыщение полюсов. С появлением насыщения
меняется форма кривой B(z), она становится более широкой и пологой, т.е.
уменьшается крутизна боковых ветвей кривой. Для расчёта линз используют семейство
аппроксимирующих поле функций B(z) = Bm [l +(z/a)2
]-m, крутизна падения боковых ветвей к-рых зависит от параметра
m. Здесь Вт - макс. индукция поля, а-параметр,
связанный соотношением a = d/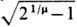
с полушириной d кривой распределения индукции поля. Полуширина d определяется следующим образом: z = d при B(z) = (1/2)Вт. Др. аппроксимирующая функция, к-рую тоже используют для ненасыщенных линз,
B(z) = Bm/ch(z/a)с полушириной d= a.arch
2, убывает по экспоненте при больших z.
Аппроксимирующие функции
позволяют вычислить оптич. параметры линз. Их подставляют в параксиальные ур-ния
траекторий электронов, вычисляют главные лучи и определяют кардинальные элементы
линз. На рис. 2, в представлены главные лучи и построение изображений
для предмета, находящегося в поле линзы: главный луч 1, касательная к
к-рому в точке плоскости предмета A(z=z0)параллельна
оси z, и луч 2, касательная к к-рому в сопряжённой точке изображения В (z
= zi) параллельна той же оси. Главная плоскость Hi проходит через точку пересечения двух касательных к главному лучу 1 в
сопряжённых точках предмета и изображения. Плоскость H0
проходит через точку пересечения таких же касательных к лучу 2. Кардинальными
элементами являются также точки мнимых фокусов F0 и Fi,
в к-рых с оптич. осью пересекаются касательные к лучам 2 и 1 в
точках предмета и изображения соответственно. Построение изображения В предмета
А производится, как и в случае 2a, с помощью касательных к реальным
лучам, состоящих из отрезков прямых, исходящих из точек предмета. Один - параллельно
оси z, другой проходит через точку фокуса F0 (рис. 2, в).
Такое построение остаётся в силе для любых координат предмета z0,
если положение кардинальных элементов фиксированное. В противном случае для
каждого положения предмета необходимо заново находить кардинальные элементы.
Существует класс полей,
в к-рых координаты кардинальных элементов не зависят от положения предмета,
находящегося, как и его изображение, в пределах поля. В Э.л. с такими полями
выполняется ур-ние Ньютона и поля этих линз наз. ньютоновыми. Из приведённых
выше аппроксимирующих функций к ньютоновым полям относится функция простого колоколообразного
поля при m=1: B(z) = Bm [l +(z/d)2]-1.
С помощью этой функции исследовано поведение сильных линз. В частности, показано,
что в пределах одного поля может быть неск. фокусов и изображений при достаточно
больших Вт и d и, следовательно, одно поле может работать
как неск. линз. Его кардинальные элементы (рис. 2, б)определяются с
помощью главных лучей 1 и 2, асимптоты к-рых параллельны оптич.
оси. Главные плоскости H0 и Hi проходят
через точки пересечения асимптот и касательных к соответствующим
лучам в реальных точках фокусов F0 и Fi.
Узловые точки находятся на главных плоскостях. Кардинальные элементы поля, работающего
как одна линза, вычисляются по ф-лам:
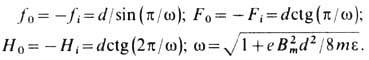
Из ф-л для фокусных расстояний
следует, что макс. оптич. сила достигается при w = 2. С помощью функции простого
колоколообразного поля получены аналитич. выражения для коэф. аберраций, напр.
установлено, что коэф. сферич. аберрации минимален при w = 2
Аппроксимирующие функции используются гл. обр. для оценки парамеров линз и не всегда пригодны для точных
расчётов. Для расчёта с высокой точностью полей, траекторий электронов, кардинальных
элементов и коэф. аберраций на ЭВМ разработаны спец. пакеты программ.
Электростатические осесимметричные
линзы делятся на иммерсионные, одиночные и катодные. Они состоят из неск.
электродов разл. формы, находящихся под разн. потенциалами. Это - диафрагмы
с круглыми отверстиями, полые цилиндры, конусы и т. п. Простейшей линзой является
о д и н о ч н а я д и а ф р а г м а, поле к-рой с одной или с двух сторон граничит
с однородными электрич. полями. В зависимости от приложенного к диафрагме потенциала
и направления примыкающих полей она может быть как собирающей, так и рассеивающей.
На рис. 3 представлено поле собирающей линзы, к к-рому с одной стороны примыкает
однородное поле. На электроде и эк-випотенциалях в условных единицах указаны
их потенциалы. За нулевой принят потенциал, при к-ром энергия электронов равна
нулю. Продольная составляющая напряжённости поля Ez тормозит,
а радиальная составляющая Er фокусирует электроны.
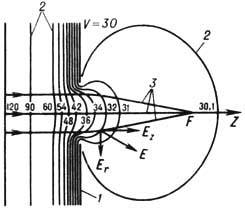
Рис. 3. Электростатическая
линза-диафрагма с круглым отверстием (собирающая): 1 - электрод-диафрагма;
2-эквипотенциальные поверхности; 3-траектории электронов; F-фокус
линзы.
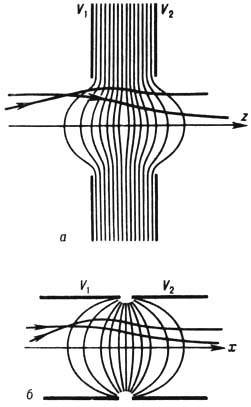
Рис. 4. Электростатические иммерсионные линзы, состоящие из двух диафрагм (а) и двух цилиндров (б). Тонкие линии - эквипотенциали, кривые со стрелками- траектории заряженных частиц, V1 и V2 - потенциалы электродов.
Э.л. наз. и м м е р с и
о н н ы м и, если потенциалы V крайних электродов разные, т. к. (по аналогии
со световой оптикой)
показатели преломления, пропорциональные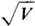 
,
в этом случае по обе
стороны линзы будут разные. На рис. 4 изображены
иммерсион. линзы с плоскими и цилиндрич. электродами.
Фокусные расстояния
и потенциалы иммерсионных линз в пространстве предметов f0,
V0 и изображений fi, Vi связаны соотношением: f0/fi= -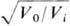
. Если оба фокусных расстояния многократно превышают осевую протяжённость поля
линзы (тонкая линза), то её оптич. силу можно вычислить по ф-ле
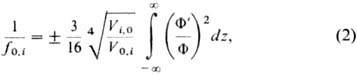
где F - осевое распределение
потенциала, Ф' - осевое распределение производной по z.
В отличие от магн. Э. л.,
в к-рых. скорость электронов меняется только по направлению, в электростатич.
линзах, напр. в иммерсионных, скорость электронов изменяется и по величине.
Последовательность иммерсионных линз, ускоряющих электроны, образует ускоритель
электронов прямого действия. Форма его электродов - цилиндрическая или коническая
(рис. 5) - экранирует электронный пучок от влияния паразитных электрич. и магн.
полей. Энергия, приобретаемая электронами в таком ускорителе, может достигать
неск. МэВ.
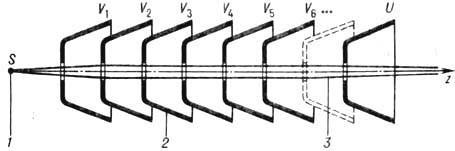
Рис. 5. Ускоритель прямого
действия, состоящий из последовательности
иммерсионных линз, электроды к-рых
в форме усечённых конусов экранируют электронный
пучок от внешних полей: 1 -источник электронов ( им
может быть кроссовер электронной пушки); 2- электроды;
3 - электронный пучок; V1, V2,
··· - промежуточные
потенциалы электродов; U-ускоряющее напряжение.
Линза, крайние электроды
к-рой имеют одинаковые потенциалы V1, наз. одиночной
(рис. 6). Потенциал среднего электрода V2 может быть
как меньше, так и больше V1. Если V2<V1, электроны пучка в начале поля линзы рассеиваются, в средней части собираются,
а на выходе снова рассеиваются. Однако общий эффект всего поля линзы - собирающий.
При V2 > V1 все происходит наоборот,
однако и в этом случае общий эффект - собирающий. Если в области седловой точки
поля (рис. 6) потенциал F ниже потенциала, при к-ром энергия электронов
равна нулю, происходит отражение электронов и линза работает как электронное
зеркало. Плоскости предмета и изображения одиночной
линзы находятся вне поля, и её кардинальные элементы
определяются так же, как в слабых магн. линзах (рис. 2, а), и так же
проводится построение изображения.
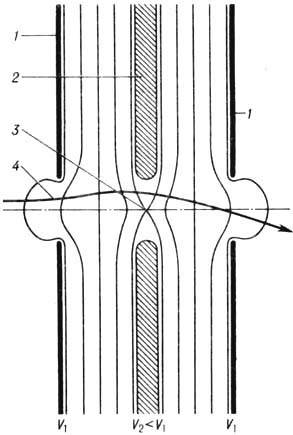
Рис. 6. Электростатическая
одиночная электронная линза:
1 - внешние электроды; 2-внутренний электрод; 3-седловая
точка; 4-траектория электрона; V1, V2-потенциалы
электродов.
В катодной линзе предмет
является катодом (источником электронов) и одновременно электродом оптич. системы.
Её наз. иммерсионным объективом, т. к. показатели преломления по обе стороны
линзы различные. В объективе происходит ускорение электронов, испущенных термо-,
фото-, автокатодом или катодом вторичной эмиссии, и формирование его изображения.
Иммерсионный объектив, состоящий из катода и анода, не может фокусировать электронные
пучки, поэтому вводят дополнит. фокусирующий электрод (рис. 7) или применяют
магн. фокусирующее поле.
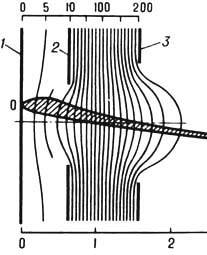
Рис. 7. Электростатическая
катодная электронная линза: 1-катод;
2 -фокусирующий электрод; 3 - анод. Тонкие линии-эквипотенциали;
О-одна из точек катода. Заштрихованное
пространство - сечение области, занятой потоком электронов, испущенных точкой
О.
Другие типы Э. л. Магн. и электростатич. цилиндрич. Э.л. фокусируют пучки заряж. частиц в одной плоскости и по своему действию подобны цилиндрич. линзам световой оптики. Электростатич. цилиндрич. Э.л. состоят из щелевых диафрагм или продольных пластин - электродов, расположенных симметрично относительно средней плоскости (рис. 8 и 9), и действуют (по аналогии с осесим-метричной оптикой) как одиночные диафрагмы или иммерсионные, катодные и одиночные линзы.
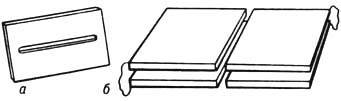
Рис. 8. Электростатические
цилиндрические электронные линзы:
а-диафрагма со щелью; б-иммерсионная линза, состоящая
из двух пластин. В области прохождения заряженных
частиц поле линз не изменяется в направлении, параллельном
щелям диафрагм или зазорам между пластинами
соседних электродов.
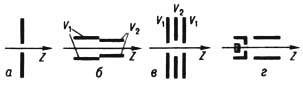
Рис. 9. Сечение электродов
электростатических цилиндрических
линз плоскостью, проходящей через ось
z перпендикулярно средней плоскости; a-цилиндрическая
(щелевая) диафрагма; б-иммерсионная
цилиндрическая линза; в-одиночная цилиндрическая
линза; г-катодная цилиндрическая линза; V1 и
V2 - потенциалы соответствующих электродов.
Поля трансаксиальных электростатич.
линз обладают симметрией вращения относительно оси (ось x на рис. 10),
к-рая перпендикулярна оптич. оси. Пучок, выходящий из точки А предмета,
после фокусировки полем линзы становится астигматическим и образует два линейных
изображения В и В'. Однако при надлежащем подборе параметров Э.
л. изображение может стать стигматическим.
Квадрупольные магн. и электростатич. линзы имеют поля с двумя взаимно перпендикулярными плоскостями симметрии. Векторы напряжённости полей в области распространения электронного пучка почти перпендикулярны скоростям электронов (рис. 11). Благодаря этому фокусирующее действие на пучки электронов многократно возрастает по сравнению с осесимметричным полем. Одна квадрупольная Э.л. не создаёт стигматич. изображения, она действует в одной меридиональной плоскости как собирающая, а в другой, ей перпендикулярной, как рассеивающая линза. Два последовательно расположенных и надлежащим образом ориентированных по азимуту квадруполя (дублет, рис. 12) создают стигматич. изображение, но с дисторсией, т. к. увеличения в двух взаимно перпендикулярных плоскостях разные. Стигматич. изображение без дисторсии получается с помощью двух дублертов. Благодаря большой оптич. силе квадрупольные системы способны фокусировать пучки заряж. частиц с большими энергиями, а в случае магн. линз - и с большими массами, чем осесимметричные системы.
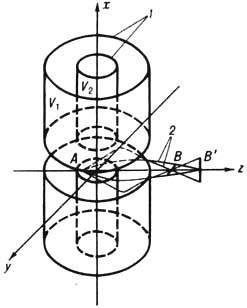
Рис. 10. Электростатическая
трансаксиальная электронная линза с электродами в виде двух соосных цилиндров
с кольцевыми щелями для прохождения пучка электронов; 1-цилиндрические
электроды; 2-траектории электронов; V1 и V2
- потенциалы электродов.
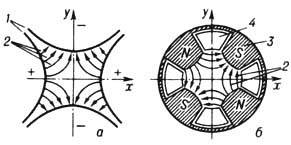
Рис. 11. Сечения квадрупольных
электростатической (а) и
магнитной (б)электронных линз, перпендикулярные направлению
движения пучка электронов: 1-электроды; 2-силовые
линии полей; 3 - магнитный полюс; 4 - обмотка
возбуждения.
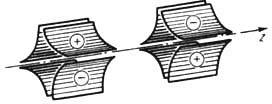
Рис. 12. Дублет из двух квадрупольных электростатических линз, поля к-рых повернуты вокруг оптической оси z системы одно относительно другого на угол 90°.
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
