Глоссарий по физике

Электронная и ионная оптика

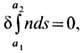
Электронная и ионная оптика - раздел физики, в к-ром изучают законы распространения пучков за-ряж. частиц - электронов и ионов - в макроскопич. магн. и электрич. полях и вопросы их фокусировки, отклонения и формирования изображений. Развитие электронной оптики (ЭО) началось с изучения катодных лучей, при помощи к-рых было получено теневое изображение объекта, свидетельствовавшее, что характер их распространения подобен распространению световых лучей в геометрической оптике. Смещение изображения под действием магн. поля показало, что катодные лучи представляют собой поток заряж. частиц [У. Крукс (W. Crookes), 1879]. Опыты по отклонению заряж. частиц совмещёнными электрич. и магн. полями привели к открытию электрона [Дж. Дж. Томсон (J. J. Thomson), 1897]. Одним из первых электронно-лучевых приборов стала осциллографич. электроннолучевая трубка (ЭЛТ) [К. Ф. Браун (К. F. Braun), 1897]. В ходе совершенствования ЭЛТ была осуществлена фокусировка электронного пучка магн. полем катушки с током [И. Е. Вихерт (I. E. Vichert), 1899]. Теоретич. и эксперим. исследования движения электронов в осесимметричном магн. поле катушки с током показали, что она пригодна для формирования электронно-оптич. изображений и, следовательно, является электронной линзой [X. Буш (Н. Busch), 1926]. Создание панцирных линз, магнито-проводы к-рых концентрируют поле катушки, а также электростатич. линз и др. устройств открыло путь к созданию электронных микроскопов, электронно-оптических преобразователей, технологич. электронно-лучевых установок и др. Конструирование спец. ЭЛТ для телевизионной и радиолокац. аппаратуры, для записи, хранения и воспроизведения информации и т. п. привело к дальнейшему развитию разделов ЭО, связанных с управлением пучками заряж. частиц. Ионная оптика (ИО) стала развиваться в связи с разработкой масс-спектрометров ,фокусирующих систем для ускорителей заряженных частиц, технологич. установок ионного травления и эпитаксии, ионных микроскопов и др. устройств.

По аналогии со световой оптикой Э. и и. о. делится на геометрическую и волновую. В геометрической Э. и и. о. предполагают, что длина волны электронов и ионов мала и не влияет на их траектории. В волновой оптике изучают вопросы, учитывающие дифракцию электронов и ионов, такие как разрешающая способность электронных микроскопов, формирование электронных и ионных зондов предельно малых размеров и т. п. В рамках геом. Э. и и. о. пучок состоит из семейства траекторий заряж. частиц, в световой геом. оптике рассматривают пучок световых лучей. Однако между световой оптикой и Э. и и. о. существует более глубокая аналогия, на к-рую впервые указал У. Гамильтон (W. R. Hamilton, 1827).

Законы геом. световой оптики являются следствием фундаментального Ферма принципа (P. Fermat, 1660), согласно к-рому световые лучи распространяются между двумя точками a₁ и а₂ по такому пути s, на прохождение к-рого затрачивается наименьшее время t. Более строго принцип Ферма формулируется как вариационная проблема

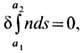
означающая, что длина оптич. пути, по к-рому распространяется свет, экстремальна.

Наименьшего действия принцип Мопертюи (Maupertuis, 1740) в механике, описывающий движение материальных тел в силовых полях, столь же универсален в ЭО и ИО, как принцип Ферма в световой. Он формулируется следующим образом:

где a₁ и а₂ - начальная и конечная точки искомой траектории заряж. частицы, а р - обобщённый импульс, приобретённый ею в электрич. и магн. полях. Для определённости речь далее пойдет об электронах, хотя все приведённые ниже соотношения справедливы и для ионных пучков при замене заряда и массы электрона на соответствующие параметры ионов. Обобщённый импульс электронов

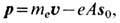
где u, e и т_е - скорость, заряд и масса движущихся электронов соответственно, А - векторный потенциал магн. поля, s₀ - единичный вектор, касательный к траектории. В выражении (1) р имеет смысл показателя преломления среды. Чтобы сделать его безразмерным, как п в оптике, обобщенный импульс относят к начальному импульсу р₀, приобретенному электронами после предварит. ускорения. Из (1) получаем выражение, аналогичное принципу Ферма:

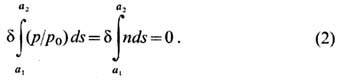
Электронно-оптич. показатель преломления п=р/р₀ в электрич. поле зависит только от координат, и такая среда для распространения электронных пучков изотропна. При наличии магн. поля (совместно с электрическим или без него) среда анизотропна, т. к. в этом случае п зависит ещё и от направления движения электронов, тогда

где т₀ - масса покоя электрона. Абсолютная величина скорости электрона зависит от потенциала поля j и её находят с помощью соотношения

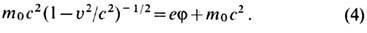
Из (3) и (4) следует:

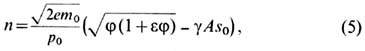
где g=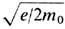 , e= е/2т₀с² - релятивистская поправка.

На принципе наименьшего действия (2) построены все осн. соотношения ЭО и ИО, включая и расчёт аберраций методом эйконала .Таким же фундаментальным соотношением для ЭО и ИО следует считать и ур-ние Лоренца, с помощью к-рого, рассматривая траектории заряж. частиц (в данном случае электронов), можно вывести те же соотношения, включая и расчёт аберраций:

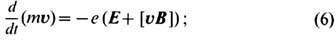
здесь Е= - gradj - вектор напряжённости электрич. поля, a B = rotA - вектор индукции магн. поля. Базовые соотношения (2) и (6) следуют одно из другого. Так, для вывода (6) из (2) нужно выражение (3) преобразовать так, чтобы неявно входящее в него время t стало независимой переменной; используем для этого соотношения

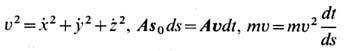
(точки над х, у, z означают производные по t). Подставляя преобразованный показатель преломления (3) в (2), получаем:

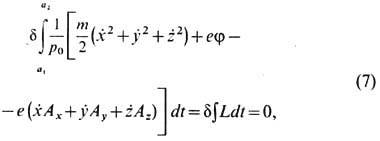
где А_х, А_у, A_z- проекции векторного потенциала А на координатные оси. Подынтегральное выражение в (7), обозначенное символом L, есть функция Лагранжа, удовлетворяющая ур-ниям Эйлера:

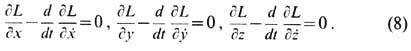
Подставляя её в (8) и объединяя три ур-ния в одно векторное, получим ур-ние Лоренца (6). Расчет траекторий с его помощью можно рассматривать как решение чисто механич. задачи движения массы под действием приложенных к ней сил. Решение той же задачи вариационным методом предпочтительнее, если упрощаются расчёты. Так, напр., для вычисления луча (траектории) в электрич. и магн. полях достаточно использовать (5) и, полагая 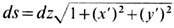, сформулировать вариационную задачу:

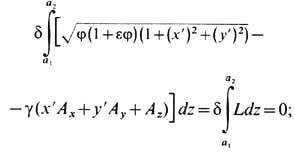
здесь штрихи означают производные по z. Затем с помощью ур-ний Эйлера (8), в к-рых t заменяется на z, можно получить искомые ур-ния луча:

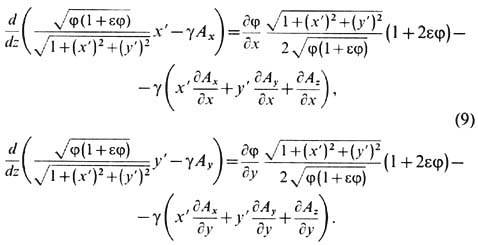
Дальнейший расчёт возможен, если известно распределение электрич. и магн. полей. При заданных краевых условиях поля вычисляются с помощью ур-ния Лапласа или с помощью ур-ния Пуассона при учёте влияния пространственного заряда. Аналитич. решение найдено лишь в нек-рых простейших случаях. Поэтому для аппроксимации экспериментально измеренных полей предложен ряд функций. Однако большинство задач решается численными методами с помощью ЭВМ. Широко используются методы сеток с прямоугольными (метод конечных разностей) и с треугольными (метод конечных элементов) ячейками. В обоих случаях вычисляют потенциалы при помощи сетки, наложенной на рассчитываемую область поля, включая границы, и формул, связывающих потенциал текущей точки расчёта с потенциалами соседних узлов сетки. Применяют также метод граничных элементов, в к-ром рассчитываются распределения плотности зарядов на электродах системы с заданными потенциалами и с их помощью определяется распределение потенциалов в области прохождения траекторий электронов.

В анализе траекторий труднее всего поддаются расчёту электронно-оптич. свойства трёхмерных полей без к--л. симметрии. Но в Э. и и. о. используются гл. обр. осесим-метричные системы, устройства с плоской симметрией или с неск. плоскостями симметрии, что определилось потребностями приборостроения. Для расчёта траекторий электронов в осесимметричной линзе можно использовать ур-ния луча (9). Они нелинейны, а из этого следует, что конический пучок с конечным углом раскрытия, исходящий из внеосевой точки плоскости предметов, не даст точечного изображения. Близкое к точечному соответствие между плоскостями предметов и изображений может быть достигнуто лишь с помощью параксиальных пучков, имеющих небольшие углы раскрытия и исходящих из малой приосевой области плоскости предметов. Искажения изображения, вызванные конечными величинами углов и расстояний от оси, рассматриваются в теории аберраций.

Ур-ния траекторий (9) в осесимметричном поле упрощаются. В частности, при осевой симметрии существует только азимутальная составляющая векторного потенциала A_q(r, z), к-рая, как и потенциал j(r, z), не зависит от азимутального угла q. Условие параксиальности пучков позволяет сделать дополнит. упрощения, использовав только первые члены разложения j и А_q в степенные ряды:

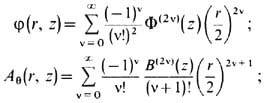
здесь Ф(z) - распределение электрич. потенциалов на оси симметрии z, B(z) - распределение магн. индукции на той же оси. После упрощений ур-ния параксиальных траекторий без релятивистской поправки (e=l) приобретают следующий вид:

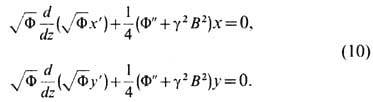
Вследствие влияния магн. поля азимутальный угол q радиальной плоскости, в к-рой перемещается электрон, изменяется, и его траектория закручивается вокруг оси z. Угол поворота плоскости

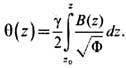
Ур-ния (10) получены в системе координат, вращающейся вместе с радиальной плоскостью. Совместив одну из координатных осей с начальным положением вращающейся плоскости и обозначив расстояние от точек траектории до оси z через s(z), получим ур-ние траектории в этой плоскости:

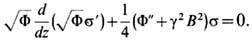
С помощью двух его частных решений, одно из к-рых w(z) не обращается в нуль ни в плоскости предмета (z = z₀), ни в плоскости изображения (z = z₁), а другое, u(z), в обоих случаях равно нулю, можно вычислить линейное М и угловое a увеличения:

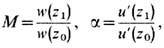
а также найти соотношение, существующее между ними:

в к-ром Ф₀ и Ф₁-потенциалы в пространстве предметов и в пространстве изображений соответственно.

Соотношение (11) аналогично соотношению между линейным и угловым увеличениями линзы в световой оптике (теорема Гельмгольца), однако оно имеет более общий характер, т. к. электронно-оптич. среда неоднородна и анизотропна.

Применение параксиальных пучков в линзах снижает точечное несоответствие между плоскостями предмета и изображения, но не устраняет его. Пучок, исходящий из точки предмета, пройдя электронную линзу, образует не сопряжённую точку изображения, а нек-рую фигуру рассеяния вокруг нее вследствие аберраций. В электростатич. линзах их пять: сферическая, кома, астигматизм, кривизна поля изображения и дисторсия. В магн. линзах к ним добавляются анизотропные кома, астигматизм и дисторсия. Структура пучков и аберрационных фигур аналогична световым. Фигуру рассеяния образуют все аберрации, кроме дистор-сии, к-рая искажает масштаб изображения. Все аберрации, кроме сферической, при неограниченном уменьшении отображаемого приосевого участка уменьшаются до нуля. Поэтому в электронных микроскопах, в к-рых отображаемый приосевой участок достаточно мал, на разрешающую способность влияет только сферическая аберрация объективной линзы. Структура пучка и образование кружка сферической аберрации показаны на рис. 1. Изображённый ход лучей (траекторий) иллюстрирует значит. возрастание преломляющей силы магн. поля B(z)линзы от ее центра к периферии, вследствие чего периферийные лучи, формирующие изображение, пересекают оптич. ось ближе к линзе, чем приосевые. В гауссовой плоскости образуется не точка, а кружок рассеяния, радиус к-рого

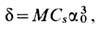
где a₀ - апертурный угол объектива, C_s - коэф. сферич. аберрации, М-увеличение. При снижении a₀ радиус кружка d быстро уменьшается, однако таким способом достигнуть сколь угодно малого кружка рассеяния не позволяют дифракц. явления.

Размер кружка рассеяния увеличивает также хроматическая аберрация, возникающая вследствие разброса электронов по энергиям. Он неизбежен, т. к. все электронные и ионные источники эмитируют электроны и ионы с разной начальной кинетич. энергией. Источники питания ускорит. систем увеличивают этот разброс. В результате часть электронов, обладающая меньшей энергией, фокусируется перед плоскостью изображения, а др. часть, с большей энергией,- за ней. В плоскости изображения образуется кружок рассеяния - отверстная хроматическая аберрация. Кроме неё существуют ещё две хроматические аберрации - увеличения и поворота (последняя - только в магн. линзах). Первая вызвана различием увеличений изображения, а вторая - различием углов поворота изображения, формируемого электронами разных энергий. Обе аберрации малы в приосевой области и исчезают на оси, поэтому на разрешающую способность влияет только отверстная хроматическая аберрация.

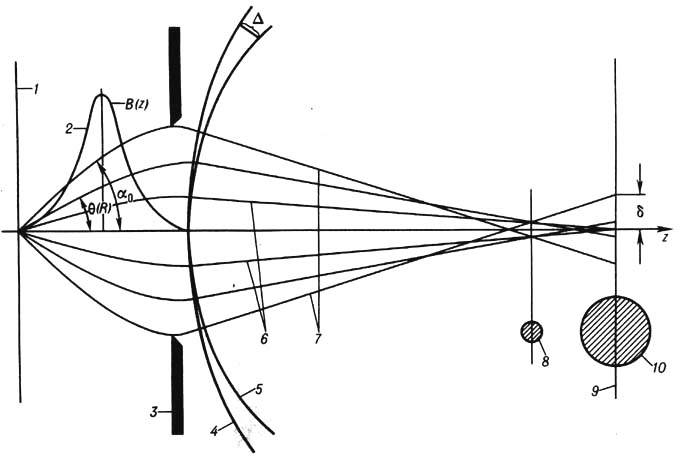
Рис. 1. Формирование структуры электронного пучка, фигур рассеяния и волнового фронта в магнитной линзе со сферической аберрацией: 1 - плоскость предмета; 2 - распределение индукции В (z)магнитного поля линзы вдоль оси z; 3 - апертурная диафрагма; 4-волновой фронт при отсутствии сферической аберрации (сферическая поверхность); 5 - реальный волновой фронт (искажён сферической аберрацией); 6-приосевые лучи; 7-периферийные лучи; 8-наименьший кружок рассеяния, радиус которого равен d/4; 9-гауссова плоскость изображения; 10 - кружок рассеяния в гауссовой плоскости изображения, радиус которого равен d = MC_sa³₀.

Поскольку разрешающая способность электронного микроскопа зависит не только от аберраций объективной линзы, но и от длины волны электронов l, корректное определение этого параметра возможно только на основе законов волновой оптики. Методом фурье-преобразова-ний наблюдаемый в микроскопе объект представляют набором структурных составляющих с разл. пространственными частотами R, воздействующими на амплитуду и фазу проходящих сквозь него волн. Обычно амплитудная компонента реальных объектов мала. Поэтому ниже рассмотрим только фазовые объекты. Волны, дифрагирующие на структурных фурье-компонентах, отклоняются на разл. углы и поэтому проходят через разл. зоны объектива, в к-рых происходит сдвиг фаз, зависящий от радиуса зоны. Изображённые на рис. 1 лучи совпадают с направлением волновых векторов дифрагированных волн (сами волны - не показаны), причём q = Rl - углы дифракции этих волн. В отсутствие аберраций линза преобразует фронт падающей волны в сферич. поверхность 4. Сферич. аберрация и дефокусировка объектива Df вызывают дополнит. сдвиги фаз, искажающие волновой фронт. Таким образом, реальный волновой фронт 5 не совпадает со сферич. поверхностью 4 и между ними существует разность хода D, возрастающая с увеличением радиуса зоны. В результате возникают сдвиги фаз между дифрагированными волнами и нулевой волной (не претерпевшей дифракцию):

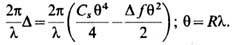
В плоскости изображения дифрагированные волны интерферируют с нулевой волной. Контраст отображённых фу-рье-компонент зависит от фаз дифрагированных волн, а частотно-контрастная характеристика фазового объекта W(R), выражающая зависимость контраста структурной составляющей от пространственной частоты, записывается след. образом:

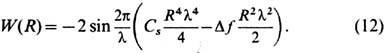
Её график представлен на рис. 2 (штриховая кривая). функция (12) выведена без учёта хроматической аберрации, в предположении освещения объекта когерентным пучком. Реальная частотно-контрастная характеристика, полученная с учётом хроматической аберрации и некогерентности освещающего объект пучка, представлена на рис. 2 сплошной линией. Это - затухающая при высоких пространственных частотах кривая, огибающие к-рой, изображенные штрих-пунктирной линией, с ростом R приближаются к оси абсцисс. Она получена для оптимальной дефокусировки Df, при к-рой предельная частота R₀ максимально сдвинута в сторону высоких частот при отсутствии глубоких провалов на промежуточных частотах. На рис. 2 видно, что структурные фурье-компоненты с пространств. частотами <R₀ передаются на изображении с контрастом одного знака. Знак контраста фурье-компоненты с частотами >R₀ начинает быстро меняться, и соответствующие этим частотам структуры передаются в искажённом виде. Предельная разрешающая способность равна наименьшему периоду d структурных фурье-компонент, передаваемых без искажений: d= 1/R₀. Апертурная диафрагма 3 (рис. 1), установленная в объективе, отсекает волны, несущие искажённую информацию об объекте.

Аберрации магн. линз меньше, чем электростатических, поэтому, напр., в электронных микроскопах используются магн. линзы. Однако в ИО электростатич. линзы незаменимы, т. к. их оптическая сила по отношению к ионам такая же, как и к электронам, и существенно превосходит оптич. силу магн. линз. Это связано с массой ионов, превосходящей массу электронов на три и более порядков величины. Отсутствие влияния массы частиц на их траектории в электростатич. оптике следует из ур-ний (10), в к-рых при В=0 масса в качестве параметра отсутствует. В магн. оптике В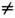0 и коэф. g, в к-рый входит масса частиц, сохраняется. Траектория частиц в этом случае зависит от их массы, что и приводит к резкому ослаблению влияния магн. поля на ионные пучки.

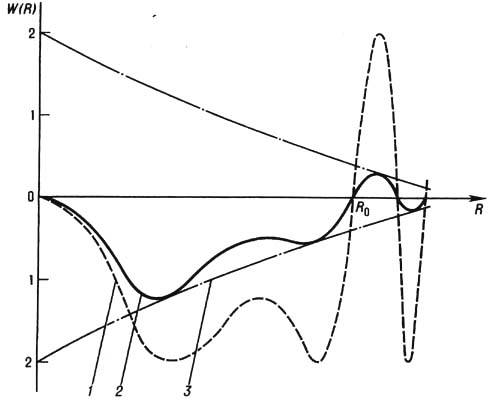
Рис. 2. Частотно-контрастная характеристика магнитной линзы: 1-при когерентном освещающем объект пучке и отсутствии хроматической аберрации; 2-при некогерентном освещающем объект пучке и влиянии хроматической аберрации; 3 - огибающие частотно-контрастной характеристики.

В ЭО и ИО кроме осесимметричных используются линзы с др. видами симметрии. Цилиндрич. линзы и электронные зеркала формируют линейные изображения точечных предметов, т. к. в ряде аналитич. приборов фокусировка нужна только в одной плоскости. В этих случаях применяют также трансаксиальные фокусирующие системы. Линзы с неск. плоскостями симметрии - квадрупольн. и ок-тупольные - применяются в ускорителях для фокусировки частиц больших энергий. Они же используются для коррекции приосевого астигматизма осесимметричных линз, в к-рых в недостаточной степени выдержана осевая симметрия. Секступольные линзы в сочетании с квадрупольными пытаются применять для коррекции сферич. и хро-матич. аберраций осесимметричных линз.

Для отклонения пучков заряж. частиц применяют системы с одной плоскостью симметрии. Они используются в ЭЛТ, в дисперсионных элементах масс-спектрометров ионов и в спектрометрах энергетич. потерь и фильтрах электронов, а также для управления электронным или ионным пучком в приборах и технол. установках. Элек-трич. поля в этих устройствах обычно формируются конденсаторами разл. форм, в т. ч. плоскими, цилиндрическими, тороидальными, сферическими и др. (рис. 3). Из разл. типов магн. полей часто применяется однородное поле, в к-ром заряж. частицы, испущенные источником (предметом) с щелевой диафрагмой в пределах небольшого угла 2a, сначала расходятся, а затем, описав траектории-полуокружности, фокусируются и формируют линейное изображение источника (рис. 4). Для улучшения фокусировки используют краевые поля, при этом краям полюсов придаётся соответствующая форма.

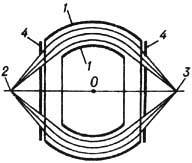
Рис. 3. Отклонение и фокусировка пучка заряженных частиц полем сферического конденсатора: 1-электроды; 2-точечный предмет; 3 -изображение предмета; 4-кольцевые диафрагмы. Изображение лежит на прямой, проходящей через источник и центр сферических электродов O.

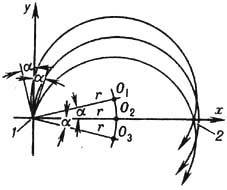
Рис. 4. Отклонение и фокусировка пучка заряженных частиц однородным магнитным полем: 1 - предмет; 2-изображение; O₁, О₂ и О₃ - центры круговых траекторийчастиц.

Методы расчёта электронно- и ионно-оптических систем, позволяющие проводить всесторонний анализ параметров спроектированных приборов и установок, достигли такого уровня, что с их помощью, с привлечением вычислит. средств и программного обеспечения, становится возможным решение проблемы синтеза создаваемых устройств - т. е. нахождения их конфигурации, др. данных, обеспечивающих реализацию заданных параметров при выполнении всех ограничит. условий (предельных габаритов, максимально допустимых напряжений, токов и т. п.). Переход от развития методов анализа электронно-и ионно-оптических систем к их синтезу станет одним из перспективных направлений развития ЭО и ИО в обозримом будущем.

Литература по

1. Брюхе Е., Шерцер О., Геометрическая электронная оптика, пер. с нем., Л., 1943; Рустерхольц А., Электронная оптика, пер. с нем., М., 1952; Глазер В., Основы электронной оптики, пер. с нем., М., 1957; Зинченко Н. С., Курс лекций по электронной оптике, 2 изд., Хар., 1961; Hanszen K.-J., Morgen-stern В., Die Phasenkontrast- und Amplitudenkontrast-Ubertragung des elektronenmikroskopischen Objektivs, "Z. Angew. Phys.", 1965, Bd 19, № 3, S. 215; Кельман В. М., Явор С. Я., Электронная оптика, 3 изд., Л., 1968; Бонштедт Б. Э., Маркович М. Г., Фокусировка и отклонение пучков в электронно-лучевых приборах, М., 1967; Hanben K.-J., Trepte L., Der Einflub von Strom- und Spannungsschwankungen, sowie der Energiebreite der Strahlelektronen auf Kontrastiibertragung und Auflosung des Elektronenmikroskops, "Optik", 1971, Bd 32, № 6, S. 519; Magnetic Electron Lenses, "Topics in Current Physics", 1982, v. 18; Хокс П., Каспер Э., Основы электронной оптики, пер. с англ., т. 1-2, М., 1993.
   

   П. А. Стоянов.

   к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  
   
   
   Знаете ли Вы, что такое "Большой Взрыв"?
   Согласно рупору релятивистской идеологии Википедии "Большой взрыв (англ. Big Bang) - это космологическая модель, описывающая раннее развитие Вселенной, а именно - начало расширения Вселенной, перед которым Вселенная находилась в сингулярном состоянии. Обычно сейчас автоматически сочетают теорию Большого взрыва и модель горячей Вселенной, но эти концепции независимы и исторически существовало также представление о холодной начальной Вселенной вблизи Большого взрыва. Именно сочетание теории Большого взрыва с теорией горячей Вселенной, подкрепляемое существованием реликтового излучения..."
   В этой тираде количество нонсенсов (бессмыслиц) больше, чем количество предложений, иначе просто трудно запутать сознание обывателя до такой степени, чтобы он поверил в эту ахинею.
   На самом деле взорваться что-либо может только в уже имеющемся пространстве.
   Без этого никакого взрыва в принципе быть не может, так как "взрыв" - понятие, применимое только внутри уже имеющегося пространства. А раз так, то есть, если пространство вселенной уже было до БВ, то БВ не может быть началом Вселенной в принципе. Это во-первых.
   Во-вторых, Вселенная - это не обычный конечный объект с границами, это сама бесконечность во времени и пространстве. У нее нет начала и конца, а также пространственных границ уже по ее определению: она есть всё (потому и называется Вселенной).
   В третьих, фраза "представление о холодной начальной Вселенной вблизи Большого взрыва" тоже есть сплошной нонсенс.
   Что могло быть "вблизи Большого взрыва", если самой Вселенной там еще не было? Подробнее читайте в FAQ по эфирной физике.

   НОВОСТИ ФОРУМА Рыцари теории эфира

   10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.