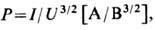
Поскольку электронный пучок является совокупностью одноимённых заряженных частиц, внутри него имеется пространственный заряд электронов, создающий собственное электрическое поле. С другой стороны, движущиеся по близким траекториям электроны можно рассматривать как линейные токи, создающие собственное магнитное поле. Электрическое поле пространственного заряда создаёт силу, стремящуюся расширить пучок ("кулоновское расталкивание"), магнитное поле линейных токов создаёт силу Ампера - Лоренца, стремящуюся сжать пучок. Расчёт показывает, что действие пространственного заряда начинает заметно сказываться (при энергиях электронов в несколько кэВ) при токах в несколько десятых мА, тогда как "стягивающее" действие собственного магнитного поля заметно проявляется только при скоростях электронов, близких к скорости света - энергии электронов порядка МэВ. Поэтому при рассмотрении электронных пучков, используемых в различных электронных приборах, технических установках, в первую очередь необходимо принимать во внимание действие собственного пространственного заряда, а действие собственного магнитного поля учитывать только для субсветовых пучков.
Основным критерием условного разделения электронного пучка на неинтенсивные и интенсивные является необходимость учёта действия поля собственного пространственного заряда электронов пучка. Очевидно, чем больше ток пучка, тем больше плотность пространственного заряда, сильнее расталкивание. С другой стороны, чем больше скорость электронов, тем меньше скажется на характере движения электронов собственное электрическое поле пучка - чем выше энергия электронов, тем "жёстче" пучок. Количественно действие поля пространственного заряда характеризуется коэффициентом пространственного заряда - первеансом, определяемым как
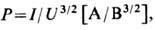
где I-ток пучка; U - ускоряющее напряжение, определяющее энергию электронов пучка.
Заметное влияние пространственного заряда на движение электронов в пучке начинает проявляться при P>=P* = 10-8А/В3/2 = 10-2 мкА/В3/2. Поэтому к интенсивным пучкам принято относить электронные пучки с Р>P*.
Неинтенсивные пучки (с Р<Р*) малого сечения, часто называемые электронными лучами, рассчитываемые по законам геометрической электронной оптики без учёта действия поля собственного пространственного заряда, формируются с помощью электронных прожекторов и используются в основном в различных электронно-лучевых приборах.
В интенсивных пучках действие собственного пространственного заряда
существенно влияет на характеристики электронного пучка. Во-первых, интенсивный
электронный пучок в пространстве, свободном от внешнего электрического и
магнитного полей, за счёт кулоновского расталкивания неограниченно расширяется;
во-вторых, за счёт отрицат. электрич. заряда электронов пучка происходит
падение потенциала в пучке. Если с помощью внешнего электрического или
магнитного полей ограничить расширение интенсивного пучка, то при достаточно
большом токе потенциал внутри пучка может понизиться до нуля, пучок "оборвётся".
Поэтому для интенсивных пучков существует понятие предельного (максимального)
первеанса. Практически при ограничении расширения пучка внеш. полями удаётся
сформировать протяжённые устойчивые интенсивные пучки с
P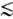
5.10
мкА/В3/2.
Полное математическое описание интенсивных электронных пучков затруднительно, поскольку реальный электронный поток состоит из множества движущихся электронов, учесть взаимодействие между к-рыми практически невозможно. При введении нек-рых упрощающих предположений, в частности, заменяя сумму сил, действующих на выбранный электрон со стороны соседних электронов, силой действия на этот электрон нек-рой электрически заряженной среды с непрерывно распределённой плотностью пространств. заряда и разбивая весь пучок на совокупность "трубок тока", удаётся с помощью ЭВМ рассчитать с достаточной для практич. целей точностью осн. параметры интенсивного пучка: форму пучка (огибающую), распределение плотности тока и потенциала по сечению пучка.
Практически применяются пучки трёх конфигураций: ленточные (плоские), имеющие в поперечном сечении вид прямоугольника с "толщиной", значительно меньшей "ширины", осесимметричные, имеющие в поперечном сечении форму круга, и трубчатые, имеющие в поперечном сечении форму кольца. Для формирования электронного пучка таких типов разработаны соответствующие электронные пушки и системы ограничения.
Влияние пространственного заряда неодинаково в пучках различной конфигурации. Наибольшее влияние на характер движения электронов на границе электронного пучка имеет составляющая напряжённости электрического поля, создаваемого пространственного зарядом, направленная перпендикулярно оси осесимметричных пучков и широкой стороне ленточных.
Радиальная составляющая напряжённости электрич. поля на границе осесимметричного пучка прямо пропорциональна току пучка и обратно пропорциональна радиусу его сечения и скорости электронов пучка. Это создаёт силу, направленную от оси, стремящуюся расширить пучок. Расталкивающая сила тем больше, чем больше ток, меньше скорость и радиус пучка. Теоретически в осесимметричных пучках траектории электронов не могут пересечь ось, а сечение пучка нельзя свести в точку, т. к. при уменьшении сечения расталкивающая сила неограниченно возрастает.
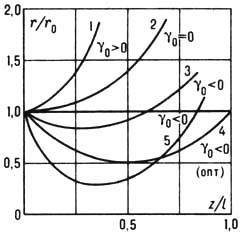
Огибающие осесимметричных электронных пучков: g0-угол входа пучка в свободное от полей пространство; r0 - начальный радиус; 1 - расходящийся пучок (g0>0); 2-цилиндрический пучок (g0=0); 3, 4, 5-сходящиеся пучки (g0<0). Пучок 4 - оптимальный, так как кроссовер (наименьшее сечение) пучка находится на самом удалённом расстоянии ( z/l=0,5) от исходной плоскости.
Огибающая интенсивного
осесимметричного пучка в пространстве, свободном от электрич. и магн. полей,
описывается зависимостью, близкой к экспоненциальной. На рис. показаны огибающие
осесимметричных пучков,
имеющих до входа в
свободное пространство цилиндрическую (кривая 2, g0 = 0), расходящуюся
(кривая 1, g0>0) и сходящуюся (кривые 3-4, g0<0)
формы (g0 - угол наклона касательной к огибающей пучка, угол
входа). Как видно на рис., пучки, первоначально сформированные как цилиндрические
(g0 = 0) и расходящиеся (g0>0), в свободном от
полей пространстве неограниченно расширяются; пучки, сформированные как сходящиеся,
вначале сжимаются (r/r0<1), проходят плоскость наименьшего
сечения (плоскость кроссовера), затем также начинают расширяться. Радиус мин.
сечения пучка - радиус кроссовера-определяется выражением
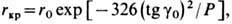
где r0
- радиус электронного пучка до входа в свободное пространство.
Радиус кроссовера тем меньше,
чем меньше первеанс и больше | g0|. С ростом (по абс. величине)
угла входа пучка в свободное от полей пространство (g0) плоскость
кроссовера сначала удаляется от исходной плоскости, за-
тем начинает приближаться
к ней (последовательно кривые 3, 4, 5). Для каждого значения первеанса существует
оптимальный "угол влёта" g0, при к-ром кроссовер
наиб. удалён от исходной плоскости, то есть электронный пучок с данным первеансом может
быть проведён на наибольшее расстояние с радиусом, не превышающим исходный.
Ленточные интенсивные пучки
в свободном от электрич. и магн. полей пространстве также неограниченно расширяются
(становятся "толще"), контур огибающей пучка описывается параболич.
законом. В отличие от осесимметричного пучка, ленточный пучок при оптимальном
входном угле теоретически может быть сведён в линию, т. е. может быть получен
линейный фокус. Пучки др. конфигураций в свободном пространстве также неограниченно
расширяются; трубчатый электронный пучок расширяется несколько меньше, чем сплошной осесимметричный.
Эксперим. проверка полученных расчётных соотношений затруднена, поскольку само понятие границы (огибающей) интенсивного пучка условно, т. к. в реальных пучках плотность тока при удалении от оси осесимметричного или от ср. плоскости ленточного пучков спадает постепенно, и границей пучка условно считается окружность или прямая, вдоль к-рой плотность тока составляет нек-рую малую долю (~0,1) её макс. величины на оси.
Падение потенциала внутри интенсивного пучка ограничивает возможность формирования протяжённого
интенсивного пучка с высоким первеансом. Тео-ретич. исследования показывают,
что в интенсивном неограниченном потоке, заполняющем пространство между двумя
плоскими параллельными проводящими поверхностями с одинаковым потенциалом, определяющим
энергию электронов потока, с увеличением тока в ср. плоскости образуется минимум
потенциала. При достижении P= 18,64 мкА/В3/2 потенциал спадает
до нуля, образуется виртуальный катод ,часть электронов проходит через
плоскость минимума, часть отражается к исходной плоскости, нормальное токопрохождение
нарушается. Эксперим. проверка подтверждает это, именно при приближении P к 18,64 мкА/В3/2 в потоке возникают неустрйчивости, колебания
электронных слоев, прохождение тока нарушается.
В реальных электронных пучках, ограниченных внешним электрическим и магнитным полями, также происходит падение потенциала, но т. к. в большинстве приборов, где используются интенсивные электронные пучки, протяжённый пучок пропускается через трубу с положит. потенциалом, на поверхности пучка удаётся поддерживать потенциал, близкий к потенциалу трубы. Но и при наличии проводящей трубы потенциал на оси осесимметричного или в ср. плоскости ленточного пучков заметно понижается, и по достижении достаточно большого первеанса (большего, чем в случае неограниченного потока) возникает неустойчивость, пучок обрывается.
Поскольку электронный пучок в свободном пространстве неограниченно расширяется, при практич. использовании интенсивных пучков кроме системы, формирующей пучок,- электронной пушки-необходима система, ограничивающая расхождение пучка. Расширение электронного пучка ограничивается с помощью внеш. электрич. и магн. полей. Классич. пример протяжённого интенсивного электронного пучка - т. н. поток Бриллюэна - цилиндрический пучок, ограниченный продольным однородным магн. полем. При определ. соотношении четырёх величин - нач. радиуса r0, тока пучка I, напряжения U0, определяющего энергию электронов до входа в магн. поле, и магн. индукции продольного однородного магн. поля B0 - теоретически возможно получить устойчивый цилиндрический электронный пучок. При оптимальном соотношении r0, I, U0 и B0 макс. первеанс бриллюэновского потока достигает 25,4 мкА/В3/2. При макс. первеансе потенциал на оси пучка составляет всего 1/3 значения на границе. При ограничении магн. полем трубчатых пучков можно получить ещё большие значения первеанса.
Практически сформировать протяжённые электронные пучки с первеансом, близким к теоретически максимально возможному, не удаётся из-за ряда причин: разброса нач. скоростей электронов, эмитированных катодом, трудности создания ограничивающих полей строго заданной конфигурации, практич. невозможностью строго выполнить нач. условия ввода пучка в систему ограничения и др. Реальные электронные пучки имеют волнистую и пульсирующую границы, форма пучка не остаётся неизменной. Поэтому для предупреждения оседания электронов пучка на поверхности пролётного канала радиус проводящей трубки, сквозь к-рую пропускается интенсивный пучок, выбирается на 20-30% больше радиуса пучка.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
