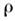в точке (х, y, z):
В макроскопической электродинамике электрический заряд тела может считаться точечным только если его поле
рассматривается на расстояниях, существенно больших, чем характерные размеры
заряженного тела.
В противном случае электрический заряд считают непрерывно распределённым в
некоторой области пространства и вводят объёмную плотность электрического заряда
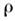в точке (х, y, z):
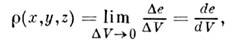
где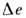
- величина заряда, находящегося в объёме
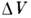в окрестности точки (x, у, z)в момент времени t. Если
электрический заряд находится в слое, толщиной которого можно пренебречь по сравнению
с характерным расстоянием, на котором рассматривается поле, то определяют
поверхностную плотность электрического заряда 
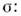
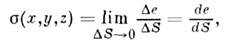
где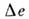
- заряд элемента поверхности
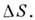Даже если заряд считается точечным, часто из соображений математического удобства
считают его непрерывно распределённым в малой области пространства. В этом
случае плотность электрического заряда является обобщённой функцией.
Если точечный заряд е находится в точке пространства r0(t), то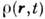
имеет вид дельта-функции Грина
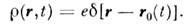
Плотность электрического заряда системы точечных зарядов определяется выражением
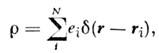
где N - полное число зарядов, ri,
еi - радиусы-векторы и величины i-x зарядов.
Введение объёмной плотности электрического заряда позволяет представить
интегральную Гаусса теорему, являющуюся одной из основных в электродинамике,
в дифференциальной форме:
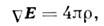
где Е - напряжённость электрического поля. Если объёмная плотность электрического заряда всюду конечна, то и вектор Евсюду конечен и непрерывен. В средах различают плотность электрического заряда свободных и связанных зарядов. Плотность электрического заряда связанных зарядов выражается через поляризации вектор Р:
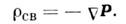
В этом случае теорема Гаусса в дифференциальной форме имеет вид
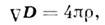
где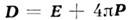
- вектор индукции электрич. поля,
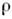- плотность свободных зарядов.
Наличие поверхностной плотности электрического заряда позволяет получить из теоремы Гаусса граничные условия для вектора Е на соответствующих поверхностях:
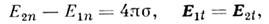
где Е1п, Е2п
- проекции поля на нормаль к поверхности, направленную от стороны
1 к стороне 2 поверхности, Et - поле, касательное
к поверхности. Левая часть первого равенства иногда наз. поверхностной
дивергенцией. С физической точки зрения скачок напряжённости электрического поля на
заряженной поверхности возникает из-за того, что точечные заряды на поверхности
создают электрическое поле, направленное в разные стороны от поверхности. Если
поверхность заряжена положительно, то поле, создаваемое
по обе стороны поверхности направлено от поверхности. В случае отрицат.
заряда поверхности поле направлено к поверхности. Поскольку реальный физический
заряд всегда сохраняется, то плотность электрического заряда удовлетворяет уравнению непрерывности:
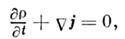
где j - вектор плотности электрического тока.
А. В. Тур, В. В. Яновский
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|
 |
