Пространственный заряд. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Пространственный заряд, объемный заряд - электрический заряд q, распределённый в объёме V так, что его плотность ρ = dq/dV конечна. Пространственный заряд определяет пространственное распределение потенциала φ и напряжённости поля E согласно уравнению Пуассона, которое для среды с постоянной диэлектрической проницаемостью ε можно записать так: Dφ = divE = -4πρ/ε. Пространственный заряд образуется, когда локальные концентрации положителных и отрицательных носителей заряда взаимно не компенсируются, а это в свою очередь связано с различием в механизмах образования заряженных частиц разного знака и различием в скоростях ухода таких частиц на границы объёма. Плотность пространственного заряда ρ = eSZ_in_i, где n_i - концентрация и Z_ie - заряд носителей данного i-того сорта; Z_i имеет знак носителя, так что для электрона или одновалентного отрицательного иона Z = -1.

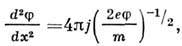
Поскольку свободные электрические заряды в пустом пространсте не могут образовать объёмную статически равновесную систему, реальные условия возникновения пространственного заряда связаны либо с процессом накопления заряда на поверхности проводника (электрическая ёмкость), либо с процессом прохождения электрического тока. Пространственный заряд образуются вблизи электродов при прохождении тока через электролит, на границе двух полупроводников с различной проводимостью, в вакууме вблизи эмитирующего электроны катода, в газовом разряде вблизи электродов, стенок, в местах с резким изменением поперечного сечения. Образованию пространственного заряда способствует наличие в среде носителей заряда с разными коэффициентом диффузии. Например, в плазме большой коэффициент диффузии электронов по сравнению с положиткльными ионами приводит к возникновению избыточного положительного заряда и, как следствие, - направленного из плазмы поля. Под действием этого поля диффузия электронов замедляется, в результате макроскопические диффузионные потоки ионов и электронов выравниваются (амбиполярная диффузия ). Пространственный заряд экранирует и внешнее электрическое поле, приложенное к плазме, препятствуя его проникновению в плазму. Вследствие такой экранировки характерная глубина проникновения электрического поля в плазму порядка дебаевского радиуса экранирования. Этот эффект определяет также значение диэлектрической проницаемости плазмы, которое меньше соответствующего значения в вакууме.

Образование пространственного заряда определяет распределение потенциала и вид вольт-амперных характеристик при прохождении тока в вакууме и отдельных областях газового разряда. Плотность пространственного заряда зависит от плотностей тока j_i и скоростей u_i соответствующих носителей заряда. Так как ток направлен от большего потенциала к меньшему, то, понимая под j_i абсолютную величину плотности тока и учитывая знак u_i, можно написать ρ = -Sj_i/u_i. При движении электронов в вакууме с нулевой начвльной скоростью на катоде скорость u_i задаётся пройденной разностью потенциалов, так что для одномерной задачи

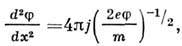
где т - масса электрона. Интегрирование этого уравнения при начальных условиях φ = 0 и E = 0 при x = 0 приводит к зависимости φ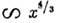

и к вольт-амперной характеристике, определяемой "законом 3/2" (см. Ленгмюра формула).

Решение аналогичной задачи для положительных ионов в газе зависит от характера движения ионов (см. Под-вижностъ электронов и ионов). В слабых полях и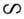E в сильных и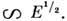 В первом случае получается j

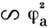, во втором j

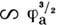. Поля, создаваемые пространственным зарядом в газе, определяют многие важные свойства разряда (временной ход развития разряда, образование стримеров, плазменные колебания и пр.). Образование пространственного заряда влияет на нарастание электронной лавины, распространяющейся в газе высокого давления. В этом случае при превышении определённого числа зарядов в лавине (~10⁶) пространственный заряд ионов, поле к-рого направлено противоположно внеш. электрич. полю, частично экранирует его и тем самым снижает эффективность размножения носителей в лавине и уменьшает скорость её распространения (см. Лавина электронная).

Пространственный заряд, возникающий при распространении пучка электронов через вакуум, служит причиной угл. расходимости пучка. В результате магн. взаимодействия электронов пучка эффект расходимости с ростом энергии электронов пучка уменьшается. При распространении электронного пучка в газе расходимость также уменьшается в связи с экранирующим действием пространственного заряда положительных ионов.

Поскольку ρ определяется алгебраической суммой зарядов разных носителей, наличие в объёме зарядов противоположных знаков может привести к частичной или полной компенсации пространственного заряда. Примерами могут служить плазма, в которой концентрации ионов и электронов почти равны, и прикатодная область в разряде с накалённым катодом, где положительные ионы практически компенсируют заряд электронов, благодаря чему падение потенциала в таком разряде невелико и почти не зависит от тока.

Уравнение Пуассона, применяющееся в указанных выше случаях, предполагает, что пространственный заряд распределён непрерывно по всему рассматриваемому объёму. В действительности поле пространственного заряда складывается из полей отдельных носителей. Поэтому приведённые зависимости φ и E есть величины, усреднённые для областей, линейные размеры которых велики по сравнению со средним расстоянием между носителями, т. е. с длиной порядка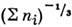

. Хаотически меняющиеся во времени локальные поля должны вычисляться непосредств. наложением полей отдельных носителей с учётом их статистического распределения.

Литература по пространственным зарядам

Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.