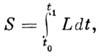
Принцип наименьшего действия. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Принцип наименьшего действия - один из вариационных принципов механики, согласно к-рому для данного класса сравниваемых друг с другом движений механич. системы действительным является то, для к-рого физ. величина, наз. действием ,имеет минимум (точнее, экстремум). Обычно принцип наименьшего действия применяется в одной из двух форм.

а) Принцип наименьшего действия в форме Гамильтона - Остроградского. В этом случае под действием за промежуток времени t₁ - t₀ понимают величину

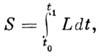
где L - функция Лагранжа, зависящая от обобщённых координат системы q_i, обобщённых скоростей ^.q_i и времени t (см. Лагранжа функция ).H. д. п. в этой форме устанавливает, что среди всех кинематически возможных перемещений системы из одной конфигурации в другую (близкую к первой), совершаемых за один и тот же промежуток времени t₁ - t₀, действительным является то, для к-рого действие S будет наименьшим. Матем. выражение принципа наименьшего действия имеет в этом случае вид

где d - символ неполной (изохронной) вариации.

б) H. д. п. в форме Мопертюи - Лагранжа. В этом случае под действием за промежуток времени t₁ - t₀, в течение к-рого система перемещается из конфигурации А в конфигурацию В, понимают величину

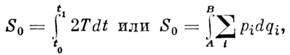
где T - кинетич. энергия системы, p_i - обобщённые импульсы. H. д. п. в этой форме устанавливает, что среди всех кинематически возможных перемещений системы из конфигурации А в близкую к ней конфигурацию В, совершаемых при сохранении одной и той же величины полной энергии системы, действительным является то, для к-рого действие S₀ будет наименьшим.

Матем. выражение H. д. п. в этом случае имеет вид

где D - символ полной вариации (в отличие от принципа Гамильтона - Остроградского, здесь варьируются не только координаты и скорости, но и время перемещения системы из одной конфигурации в другую). Принцип наименьшего действия в форме (2) справедлив только для консервативных и притом голономных систем. Принцип наименьшего действия в форме (1) является более общим и, в частности, может быть распространён на неконсервативные системы. H. д. п. пользуются для составления ур-ний движения механич. систем и для исследования общих свойств этих движений. При соответствующем обобщении понятий принципа наименьшего действия находит приложения в механике непрерывной среды, в электродинамике, квантовой механике и др.

Литература по принципу наименьшего действия

Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, "мысленный эксперимент" фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей "мысленных экспериментов" является обман слушателя или читателя путем замены настоящего физического эксперимента его "куклой" - фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, "мысленными экспериментами" привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие "фантики" от настоящих ценностей.

Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").

Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.

Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.