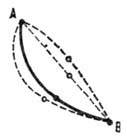
Брахистохрона. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Брахистохрона (от греч. brachistos - кратчайший и chronos - время) - кривая быстрейшего спуска, т. е. та из всевозможных кривых, соединяющих 2 данные точки А и В (см. рис.) потенциального силового поля, двигаясь вдоль которой под действием только сил поля с нач. скоростью, равной нулю, материальная точка придёт из положения А в В за кратчайшее время. При движении в однородном поле силы тяжести брахистохрона - циклоида с горизонтальным основанием и точкой возврата, совпадающей с точкой А. Решение задачи о брахистохроне послужило отправным пунктом для развития вариационного исчисления.

Брейта - Вигнера формула - описывает поведение сечения ядерной реакции или реакции между элементарными частицами вблизи резонансного значения энергии в случае изолир. резонанса (когда его ширина много меньше расстояния по энергии до др. резонансов с теми же квантовыми числами). Предложена Г. Брейтом (G. Breit) и Ю. Вигнером (E. Wigner) в 1936; наз. также дисперсионной ф-лой ввиду сходства с выражением, описывающим дисперсию света.

При взаимодействии налетающей частицы с ядром - мишенью - может образоваться составное ядро - нестабильная ядерная система, обладающая рядом квазистационарных уровней. Ширина уровня Г связана с временем жизни,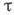

квазистационарного состояния соотношением

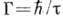. Если энергия частицы в системе центра инерции близка к энергии

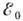одного из уровней составного ядра, то вероятность образования составного ядра становится особенно большой, и сечения ядерных реакций резко возрастают, образуя резонансные максимумы. При этом (в случае изолир. резонанса) сечение реакции и определяется брахистохроной - Брейта - Вигнера формулой. Аналогичная ситуация имеет место при взаимодействии элементарных частиц, если их полная энергия в системе центра инерции (масса системы) близка к массе нестабильной частицы - резонанса с подходящими квантовыми числами (спином, чётностью, странностью и т. д.).

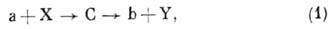
идущую через составное ядро (или резонанс) С со спином I^С. Если во входном (а+Х) и выходном (b+Y) каналах орбитальный момент l=0, то брахистохрона - Брейта - Вигнера формула для сечения реакции вблизи энергии резонанса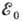

имеет вид (рис. 1,2):

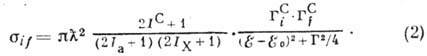
Здесь индексы i и f обозначают входной и выходной каналы,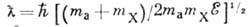

-длина волны де Бройля; 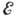- кинетич. энергия частиц а и X в системе центра инерции; m_a, I_а, т_X, I_X- массы и спины частиц а и X;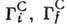

- парциальные ширины уровня составного ядра С, связанные с вероятностями его распада по каналам i и f, -полная ширина уровня.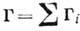

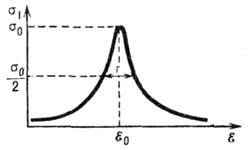
Рис. 1. Зависимость сечения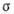

резонансного рассеяния от энергии падающей частицы

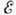в случае l=0.

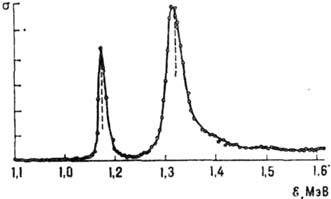
Рис. 2. Ход сечения s реакции ¹⁴С(р, n)¹⁵N; два максимума отвечают двум уровням энергии составного ядра ¹⁶N.

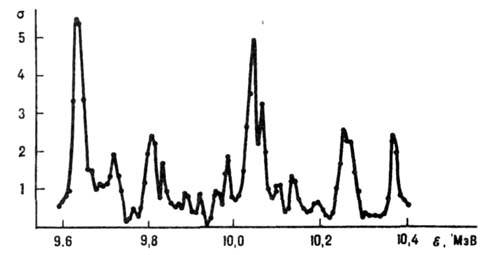
Рис. 3. Эриксоновские флуктуации в ходе сечения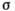

реакции ³⁵Сl(р,

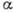)³²S.

Ядерные ширины меняются в зависимости от энергии возбуждения и массы ядра в пределах от 0,1 эВ до сотен кэВ. Для элементарных частиц полные ширины лежат в интервале от неск. десятков кэВ до сотен МэВ. Парциальные ширины не зависят от способа образования составного ядра. Ширины сами являются функциями энергии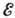

. Обычно, когда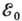

не мало, этим можно пренебречь. Если же

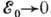, то следует учитывать, что

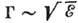. Ф-ла (2) справедлива и при

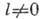, если в набор квантовых чисел, описывающих каналы i и f, включать спины и орбитальные моменты каналов. Брейт-вигнеровскому поведению сечения (2) с теоретич. точки зрения отвечает полюсная особенность амплитуды процес-

са на нефиз. листе при

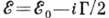(см. Матрица рассеяния). Предположения о наличии такой особенности вместе с условием унитарности оказывается достаточным для получения брахистохроны - Брейта - Вигнера формулы, причем наличие особенности в одном из каналов автоматически приводит к такой же особенности во всех связанных с ним каналах. Тот факт, что полюс амплитуды рассеяния расположен на нефиз. листе, выражается в непостоянстве Г. Амплитуда реакции, соответствующая брахистохрона - Брейта - Вигнера формула, имеет вид (для орбитального квантового числа l=0):

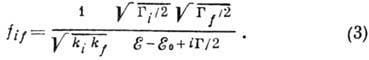
Здесь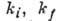

- импульсы относит. движения частиц в каналах i и f. Разбиение числителя в (3) на множители, соответствующие разным каналам, отвечает процессу столкновения, происходящему в 2 стадии: образования составного ядра в определ. квазистационарном состоянии и его распада по тому или иному каналу. В случае упругого рассеяния следует учитывать нерезонансный фон, называемый обычно потенциальным рассеянием. Если резонанс осуществляется в волне с орбитальным моментом , то амплитуда упругого рассеяния

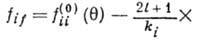
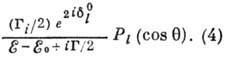
Здесь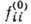

- амплитуда потенциального рассеяния,

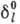- фаза потенциального рассеяния,

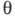- угол рассеяния, P_l - полином Лежандра.

Брейта - Вигнера формула, являющаяся одним из первых количественных результатов теоре-тич. ядерной физики, сыграла важную роль в развитии ядерной физики и физики элементарных частиц. В ядерной физике она применяется во всех случаях, когда уровни составного ядра не перекрываются [1, 2].

При исследовании элементарных частиц - резонансов их наиб. строгим определением является наличие брейт-вигнеровской особенности в амплитуде рассеяния в состоянии с определ. значениями полного момента, чётности, изоспина и др. квантовых чисел. Непосредств. применение брахистохроны - Брейта - Вигнера формулы при анализе взаимодействий элементарных частиц, как правило, затруднено из-за нерезонансного фона и большой ширины резонансов. В таких случаях наличие резонансов определяется по петлям на т. н. диаграмме Аргана [3].

Брахистохрона - Брейта - Вигнера формула может быть обобщена на случай перекрывающихся уровней [4, 5]. В этом случае полная ширина уровня

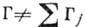. На этом пути получено описание т. н. входных состояний, отвечающих широкому резонансу на фоне множества узких [5]. Если ширина Г уровней гораздо больше, чем расстояние между соседними уровнями, то в энергетич. и угловой зависимости сечений ядерной реакции возникает тонкая структура нерезонансного типа (эриксоновские флуктуации, рис. 3). Их исследование даёт информацию о ср. ширине Г перекрывающихся уровней [6].

Литература по брахистохроне

Знаете ли Вы, что электромагнитное и другие поля есть различные типы колебаний, деформаций и вариаций давления в эфире.

Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.

В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.