Дислокация в кристаллах (от ср--век. лат. dislocatio - смещение, перемещение) - дефекты
кристаллич. решётки, искажающие правильное расположение атомных (кристаллографич.)
плоскостей (см. Кристаллическая решётка). Д. отличаются от др. дефектов в кристаллах тем, что значит. нарушение регулярного чередования атомов сосредоточено
в малой окрестности нек-рой линии, пронизывающей кристалл.
Типы дислокаций. Простейшими
видами Д. являются краевая и винтовая Д. В идеальном кристалле соседние
атомные плоскости параллельны на всём своём протяжении; если одна из атомных
плоскостей обрывается внутри кристалла (рис. 1, а), возникает краевая Д., край
"лишней" полуплоскости является её осью.

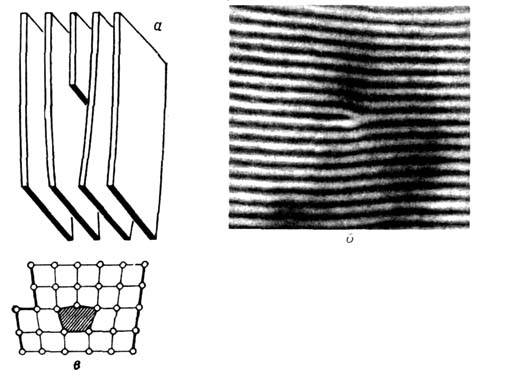
Рис. 1. Краевая дислокация:
а - обрыв атомной плоскости; б - электронно-микроскопическое изображение
дислокации в кристалле; в - схема расположения атомов в ядре Д.
Применение электронных
микроскопов с большой разрешающей способностью позволяет непосредственно
наблюдать в нек-рых кристаллах специфичное для краевой Д. расположение атомных
рядов (рис. 1, б). Область нерегулярного расположения атомов на
линии Д., вытянутая вдоль её оси и имеющая поперечные размеры порядка неск.
межатомных расстояний, наз. ядром Д. Нек-рое представление о характере нарушений
регулярности кристаллич. решётки вблизи ядра Д. в металлах может быть получено
при изучении изображений дефектной части кристалла, возникающих на экране ионного
микропроектора. На рис. 1, в атомы ядра Д. условно расположены по контуру
заштрихованного пятиугольника. Одновременно на рис. 1, в показано, что
краевая Д. может быть получена в результате незавершённого сдвига верх. части
кристалла на один период кристаллич. решётки вдоль плоскости, проходящей через
ось Д. Направление сдвига, создающего краевую Д., перпендикулярно её оси.
Винтовую Д. можно представить
себе как результат сдвига на период решётки одной части кристалла относительно
другой вдоль нек-рой полуплоскости параллельно её краю, играющему роль оси Д.
(рис. 2, а). T. о., порождающий винтовую Д. сдвиг параллелен её оси.
В случае винтовой Д. ни одна из атомных плоскостей не оканчивается внутри кристалла,
но сами плоскости, являясь только приблизительно параллельными, смыкаются в
одну винтовую поверхность. Если ось винтовой Д. выходит на внеш. поверхность
кристалла, то на последней образуется характерная ступенька высотой
в толщину одного атомного слоя. При кристаллизации атомы легко присоединяются
к ступеньке на поверхности растущего кристалла (рис. 2, б), смещают край
ступеньки, вызывая её закручивание вокруг оси Д. Ступенька последовательно поднимается
с одного "кристаллич. этажа" на другой, что приводит к спиральному
росту кристалла (рис. 2, в).
Между предельными типами
краевой и винтовой Д. возможны любые промежуточные, в к-рых линия Д. не обязательно
прямая: она может представлять собой произвольную плоскую или пространственную
кривую. Порождающий Д. сдвиг описывается постоянным вдоль линии Д. вектором
Бюргерса b, совпадающим с одним из трансляц. периодов кристаллич.
решётки. Плоскость, проходящая через b и касающаяся линии Д. в
рассматриваемой точке, наз. плоскостью скольжения данного элемента Д. Возможные
системы плоскостей скольжения определяются структурой кристаллич. решётки. Огибающая
плоскостей скольжения всех элементов Д. наз. её поверхностью скольжения (цилиндрич.
поверхность, образующие к-рой параллельны b, а направляющей служит линия
Д.). Линии Д. не могут обрываться внутри кристалла и должны либо быть замкнутыми
(петли Д.), либо выходить на поверхность кристалла, либо разветвляться на др.
Д. В последнем случае образуется сетка Д., в каждом узле к-рой выполняется закон
сохранения вектора Бюргерса: сумма векторов Бюргерса Д., входящих в узел, равна
сумме векторов Бюргерса Д., выходящих из узла.
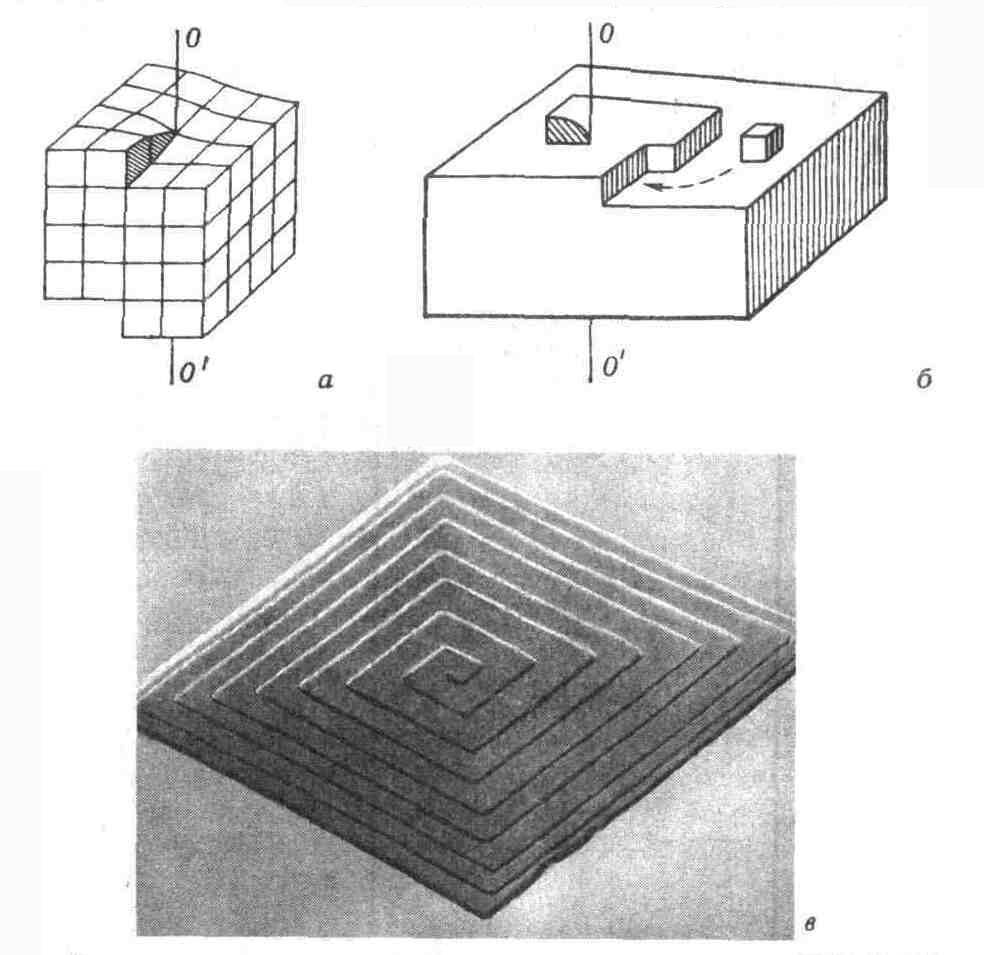
Рис. 2. Винтовая дислокация,
а - схема расположения атомов (кубик) в кристалле с дисклокацией; б - поверхность кристалла с выходом винтовой дислокации; в - спираль
роста в кристалле парафина, возникшая на выходе винтовой дислокации.
Кол-во Д. в кристалле характеризуется
их плотностью, к-рая определяется как ср. число линий Д., пересекающих проведённую
внутри тела единичную площадку. Плотность Д. колеблется от 102-103
см-2 в наиб. совершенных монокристаллах до 1011- 1012
см-2 в сильно искажённых (холоднообработанных) металлах.
Дислокации в теории
упругости. Внутри ядра любой Д. смещение атомов из своих равновесных положений
в идеальном кристалле - порядка величины межатомных расстояний и существенно
зависит от типа и конкретных свойств кристалла. Если же окружить ядро Д. нек-рой
трубкой, то вне этой трубки кристалл может считаться идеальным и подверженным
только малой упругой деформации. Поэтому искажение кристалла вдали
от оси Д. может быть проанализировано методами упругости теории, к-рые
заменяют Д. геом. линией. Д. характеризуется величиной и направлением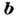 и единичным вектором касательной
и единичным вектором касательной 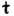 к
её линии. Распределение пары векторов
к
её линии. Распределение пары векторов 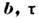 позволяет описывать любое распределение Д. в кристалле.
позволяет описывать любое распределение Д. в кристалле.
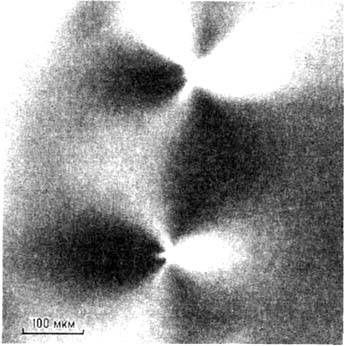
Рис. 3. Поля упругих напряжений вокруг краевых дислокаций в кристалле Si, выявленные по наблюдению фотоупругости; линии дислокации перпендикулярны плоскости рисунка.
Д. порождают вокруг себя
упругие деформации и напряжения, поэтому являются источниками упругих полей
в кристалле (см. Упругость ).Упругие деформации вокруг Д. по своему распределению
в кристалле напоминают магн. поле пост. тока, контур к-рого совпадает с линией
Д., а сила к-рого пропорц. b. Напр., у винтовой Д., направленной по оси
z, поля тензора деформаций 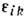 и тензора напряжений
и тензора напряжений 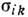 имеют следующие отличные от нуля компоненты в цилиндрических координатах
имеют следующие отличные от нуля компоненты в цилиндрических координатах 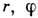 :
:
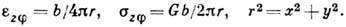 :
:
Здесь G - модуль
сдвига (см. Модули упругости). Поле напряжений обусловливает собственную
упругую энергию Д., пропорц. b2 и по порядку величины равную
10-4 эрг на 1 см её длины. Поля напряжений вблизи отд. Д. в прозрачных
кристаллах наблюдаются с помощью поляризов. света (рис. 3; см. Поляризационнооптический
метод исследования напряжений). Наличие упругих полей приводит к взаимодействию
Д., похожему на взаимодействие контуров с пост. током. Это взаимодействие определяет
равновесное распределение Д. в дислокац. скоплениях. Форма скопления Д. в плоскости
скольжения характеризует свойства незавершённой полосы сдвига. Устойчивое скопление
прямолинейных краевых Д. в слое, перпендикулярном плоскости скольжения, наз.
дислокационной стенкой и вызывает разориентацию кристаллич. блоков, т. е. моделирует
границу блоков в кристалле (рис. 4).
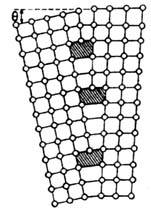
Рис. 4. Граница разориентировавных
блоков, образованная краевыми дислокациями.
Д. как источник упругого
поля испытывает действие силы, обусловленной сдвиговыми напряжениями в кристалле
и напоминающей силу действия магн. поля на проводник с током. Величина силы,
приложенной к единице длины линии Д., равна 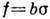 , где
, где 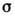 - соответствующая
сдвиговая компонента тензора напряжений
- соответствующая
сдвиговая компонента тензора напряжений 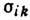 . Напр., если краевая Д. параллельна оси z и ее вектор
b направлен по оси z, то
. Напр., если краевая Д. параллельна оси z и ее вектор
b направлен по оси z, то 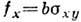 . Равновесная форма Д. определяется условием равенства силы f и сил неупругого
происхождения, аналогичных силам трения.
. Равновесная форма Д. определяется условием равенства силы f и сил неупругого
происхождения, аналогичных силам трения.
Дислокация и пластичность
кристаллов. Под действием сдвиговых напряжений Д. могут перемещаться в кристалле,
вызывая его пластич. деформацию (рис. 5). Если в движение вовлечено большое
число Д., то скорость пластич. деформации 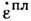 прямо пропорц. плотности
прямо пропорц. плотности 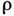 движущихся Д. и их ср. скорости v:
движущихся Д. и их ср. скорости v: 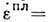
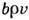 , где b - величина вектора Бюргерса отдельной Д.
, где b - величина вектора Бюргерса отдельной Д.
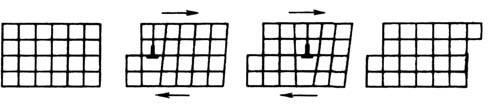
Рис. 5. Схема пластической
деформации в результате скольжения дислокации.
T. о., Д.- носители пластичности монокристалла. Многие проявления пластичности кристаллов связаны с разл.
видами движения отд. Д. или целых их рядов и скоплений.
Расположение атомов в ядре
краевой Д. приводит к выводу, что её перемещение на 1 атомный шаг вдоль плоскости
скольжения связано с малыми относит. перемещениями атомов в ядре Д. Поэтому
скольжение Д. должно происходить при сравнительно малых внеш. нагрузках. Напряжения,
при к-рых начинается скольжение Д., определяют микроскопич. предел упругости
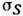 монокристалла; при достижении такой сдвиговой нагрузки кристалл теряет упругость,
в нём начинается пластич. деформация. Величина
монокристалла; при достижении такой сдвиговой нагрузки кристалл теряет упругость,
в нём начинается пластич. деформация. Величина 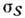 оказывается в 102-104 раз меньше модуля сдвига монокристалла
G. При отсутствии Д. идеальный монокристалл не должен обладать пластичностью
вплоть до напряжений 0,1 G. T. о., обусловленная скольжением Д. малая
величина
оказывается в 102-104 раз меньше модуля сдвига монокристалла
G. При отсутствии Д. идеальный монокристалл не должен обладать пластичностью
вплоть до напряжений 0,1 G. T. о., обусловленная скольжением Д. малая
величина 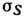 является
физ. причиной того, что сдвиговая прочность реальных кристаллов с Д. на неск.
порядков ниже таковой для бездислокац. монокристаллов. Сдвиговую прочность,
близкую к предельной, могут иметь лишь тончайшие нитевидные кристаллы ,толщины
к-рых измеряются мкм и к-рые часто образуются путём спирального роста вокруг
одиночных винтовых Д.
является
физ. причиной того, что сдвиговая прочность реальных кристаллов с Д. на неск.
порядков ниже таковой для бездислокац. монокристаллов. Сдвиговую прочность,
близкую к предельной, могут иметь лишь тончайшие нитевидные кристаллы ,толщины
к-рых измеряются мкм и к-рые часто образуются путём спирального роста вокруг
одиночных винтовых Д.
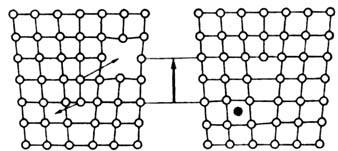
Рис. 6. Переползание краевой дислокации, сопровождающееся изменением числа точечных дефектов в кристалле.
Скольжение Д. не вызывает
локального изменения объёма или плотности кристалла и поэтому наз. консервативным
движением. Существует неконсервативное движение Д., или переползание, при к-ром
краевая Д. смещается в направлении, перпендикулярном плоскости скольжения. Переползание
связано с неупругим изменением плотности кристалла вдоль линии Д. и происходит
путём "наращивания" или "растворения" атомных рядов
на краю "лишней" атомной полуплоскости, что, в свою очередь, сопровождается
образованием или исчезновением вакансий и межузельных атомов (рис.
6). Если переползание вызвано постоянным сдвиговым напряжением, то связанный
с этим перенос материала осуществляется за счёт диффузии атомов или вакансий
из кристалла к линиям Д., и направление диффузионных потоков задаётся тензором
напряжений. T. к. коэф. диффузии резко уменьшаются с понижением температуры, то
переползание Д. с заметной скоростью происходит только при достаточно высоких
темп-pax. Согласованное переползание системы Д. обеспечивает механизм дислокационно-диффузионного
течения кристаллов.
Развитие пластич. деформации,
связанное с перемещением Д., существенно определяется скоростью их движения
(подвижностью) и интенсивностью образования (зарождения) подвижных Д. Подвижность
Д. в предельно чистых и совершенных кристаллах зависит от характера сил межатомных
связей, от взаимодействия с фононами и электронами проводимости (в
металлах). Подвижность Д. в неидеальных кристаллах уменьшается за счёт их взаимодействия
друг с другом и с др. дефектами, к-рое приводит к торможению или застопорению
движущихся Д. и вызывает упрочнение кристалла при деформировании. Но оно же
приводит к возникновению новых Д., без чего невозможно обеспечить значит. пластич.
деформацию. Если бы новые Д. не рождались в кристалле, то пластич. деформация
прекратилась бы после выхода на поверхность тела всех подвижных Д. При повышении
внеш. напряжений интенсивность размножения Д. увеличивается, и ср. расстояния
между Д. сокращаются. Возникает дислокационная структура, к-рая либо полностью
препятствует движению Д. (тогда дальнейший рост нагрузки приводит к разрушению
кристалла путём зарождения и распространения микротрещин), либо придаёт движению
Д. кооперативный характер, обеспечивающий очень большие пластич. деформации
(кристалл может перейти в состояние сверхпластичности).
Взаимодействие дислокации
с дефектами кристаллической решётки. Упругое взаимодействие Д. с точечными дефектами
(примесными атомами и вакансиями) приводит к повышению концентрации последних
вблизи оси Д. и образованию вокруг неё т.н. облаков Котрелла. Сгущение атмосферы
Котрелла в перенасыщенных твёрдых растворах может привести к коагуляции примесей
на Д. В прозрачных кристаллах это приводит к "декорированию" Д.,
что делает их визуально наблюдаемыми (рис. 7). Осевшие на Д. примеси блокируют
её движение, как бы "пришпиливая" в нек-рых точках линию Д. В реальных
условиях отрыв от примесей является осн. механизмом преодоления препятствий
движению Д. (стопоров). При высоких темп-pax Д. преодолевает стопоры термоактивац.
путём, при низких темп-pax возможны процессы квантового туннелирования.

Рис. 7. Сетка дислокаций
в кристалле KCI, декорированных
Ag (размер ячейки порядка
неск. мкм).
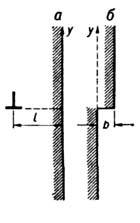
Рис. 8. Образование ступени
роста при выходе дислокации на поверхность кристалла .
Взаимодействие с др. Д.
может быть как упругим, так и контактным, когда при скольжении пересекается
"лес" Д. разных ориентации. Пересечение двух разных систем порождает
изломы на линиях Д., не способные к скольжению при том же характере внеш. нагрузки
и перемещающиеся путём переползания. В результате включается диффузионное взаимодействие
Д. с точечными дефектами. В случае переползания большого числа участков Д. в
кристалле может возникнуть неравновесная концентрация вакансий. Наоборот, при
избытке вакансий в
кристалле (в процессе отжига или при облучении) может происходить их коагуляция
в плоские дискообразные полости, после "захлопывания" к-рых образуются
кольцевые краевые Д.
Д. взаимодействует с межзёренными
границами в поликристаллах и со свободной поверхностью монокристалла
(рис. 8, а). При выходе Д. на внеш. поверхность на последней образуется ступенька
роста (рис. 8, б). В распадающихся сплавах Д. взаимодействует
с макроскопич. включениями новой фазы. Контактное взаимодействие с протяжёнными
дефектами может фиксировать нек-рые участки Д., изменяя характер её движения:
скользящая Д. "переползает" в др. параллельную плоскость скольжения,
происходит поперечное скольжение в плоскости, наклонённой к исходной, возникают
замкнутые петли Д., проявляющие себя как источники Д.
Дислокации в физические
свойства кристаллов. Д. влияют в первую очередь на механич. свойства твёрдых
тел (упругость, пластичность и прочность), для к-рых их присутствие часто является
определяющим. Упругие поля Д. изменяют оптич. свойства кристаллов, на чём основан
метод наблюдения изолированных Д. в прозрачных материалах (рис. 3). T. к. упругие
напряжения сравнительно легко вовлекают Д. в движение, то в случае интенсивных
тепловых колебаний кристалла (см. Колебания кристаллической решётки)
Д. периодически смещаются из своих равновесных положений и часть энергии
колебаний идёт на их перемещение. Но т. к. движение Д. сопровождается определ.
торможением, то Д. рассеивают колебат. энергию, давая ощутимый вклад во внутреннее
трение в твёрдых телах.
Нарушение регулярности
кристаллич. решётки в ядре Д. приводит к тому, что в местах выхода линий Д.
на внеш. поверхность тела хим. стойкость кристалла ослабляется и спец. реагенты
способны разрушать окрестность оси Д. В результате обработки поверхности кристалла
таким травителем в местах выхода Д. образуются видимые ямки. Метод избират.
травления является основным для непосредств. наблюдения отдельных Д. в массивных
образцах непрозрачных материалов (рис. 9).

Рис. 9. Дислокации в кристалле
KCl, выявленные методом травления; дислокационное скопление в полосе скольжения
пересекает границу блоков (наклонный ряд ямок травления).
Возникновение системы "оборванных"
атомных связей в ядре Д. выделяет линию Д. в отношении электрических, магн.
и оптич. свойств, в частности Д. может нести или захватывать электрич. заряд
и обладать намагниченностью, отличной от ср. намагниченности кристалла. Наличие
Д. повышает электросопротивление проводников и изменяет концентрацию свободных
носителей заряда в полупроводниках. Значит. роль играют Д. в магн. кристаллах,
существенно определяя разл. релаксац. явления.
Д. косвенно влияют на свойства
кристаллов, зависящие от характера распределения и перемещения в них точечных
дефектов (примесей, вакансий, центров окраски и др.). Во-первых, при определ.
характере движения Д. испускает или поглощает вакансии, изменяя их общее кол-во
в кристалле. Динамич. образование заряж. вакансий в ионных кристаллах и полупроводниках
может сопровождаться люминесценцией. Во-вторых, скорость диффузионного перемещения
точечных дефектов вдоль оси Д., как правило, больше, чем скорость их диффузии
через объём регулярного кристалла. Коэф. линейной диффузии вдоль Д. может на
неск. порядков превышать коэф. объёмной диффузии (см. Диффузия). Поэтому
Д. играют роль "дренажных трубок", по к-рым точечные дефекты довольно
легко могут перемещаться на большие расстояния в кристалле.

А. И. Косевич
|
|