
Фонон - квант колебаний
атомов кристаллич. решётки. Термин введён И. Е. Таммом по аналогии с квантом
эл--магн. поля-фотоном .Рассмотрение колебаний кристаллич. решётки основано
на адиабатическом приближении, в рамках к-рого совокупности её структурных
элементов (атомов, молекул, ионов) можно приписать потенц. энергию, зависящую
от координат ядер. Эта энергия разлагается в ряд по степеням малых смещений
ядер из их положения равновесия. Обычно в кристаллах смещения атомов малы вплоть
до температуры плавления. Поэтому можно ограничиться гармонич. приближением, т.
е. в разложении энергии оставить только квадратичные по смещениям слагаемые.
В гармонич. приближении
динамич. состояние кристалла описывается совокупностью нормальных колебаний (волн). Каждое нормальное колебание определяется значением волнового вектора
k, частота волны w является функцией k. В кристалле,
элементарная ячейка к-рого содержит r атомов, существует 3r типов разл. нормальных колебаний, отличающихся друг от друга не только зависимостью
w(k), но и поляризацией колебаний (см. Колебания кристаллической
решётки). В гармонич. приближении ко-лебат. энергия кристалла-сумма энергий
нормальных колебаний.
Каждому нормальному колебанию
можно поставить во взаимно однозначное соответствие осциллятор с частотой
wi. Тогда колебат. часть энергии кристалла равна сумме энергий
осцилляторов:

Согласно квантовой механике,
энергия осциллятора квантуется:
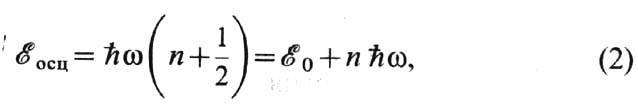
где п = 0, 1,
2, ... - целые числа, а 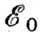 -энергия
нулевых колебаний. Согласно ф-ле Планка (см. Планка закон излучения)., ср. энергия осциллятора при температуре Т равна
-энергия
нулевых колебаний. Согласно ф-ле Планка (см. Планка закон излучения)., ср. энергия осциллятора при температуре Т равна
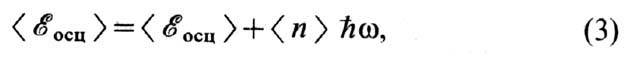
где
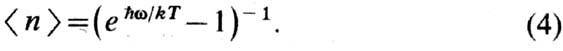
Приведённые ф-лы позволяют
ввести квазичастицы - Ф., считая, что п-число Ф. i-го сорта с
квазиволновым вектором k. Квазиимпульс р и энергия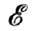 Ф.
равны
Ф.
равны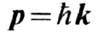 ,
, 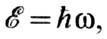 где
k и w- волновой вектор и частота соответствующей волны нормальных
колебаний решётки. Скорость Ф. равна групповой скорости волны колебаний
где
k и w- волновой вектор и частота соответствующей волны нормальных
колебаний решётки. Скорость Ф. равна групповой скорости волны колебаний
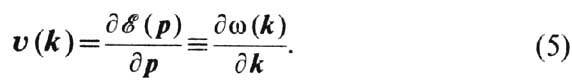
Зависимость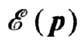 наз. законом дисперсии Ф. Ср. число Ф. сорта i
наз. законом дисперсии Ф. Ср. число Ф. сорта i
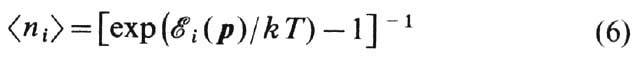
можно трактовать как равновесную
функцию распределения Ф. i-го сорта в импульсном p-пространстве.
Она совпадает с функцией распределения Бозе с химическим потенциалом m=0. Последнее означает, что Ф. являются бозонами. Равенство
m=0-следствие того, что число Ф. не сохраняется, а в равновесии зависит от температуры.
Среди 3r типов Ф.
есть 3 типа акустич. Ф., энергия к-рых при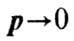 линейно зависит от р:
линейно зависит от р:
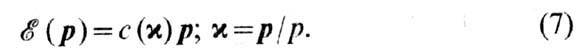
Здесь с-скорость
звука, зависящая от направления. Если r>1, то 3r-3 типов Ф.
соответствуют оптич. колебаниям кристалла. Макс. энергия Ф. порядка kQД,
где QД-Дебая температура. Газ фононов. Колебат. часть
энергии кристалла (отсчитанная от энергии нулевых колебаний) в гармонич. приближении
равна сумме энергий Ф.:
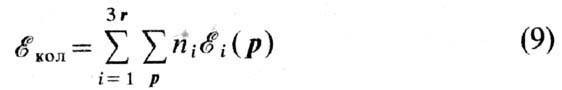
(суммирование по р
сводится к интегрированию по ячейке импульсного пространства, см. ниже).
Соотношение (8) означает, что колебат. состояние кристалла в гармонич. приближении
может быть представлено в виде идеального газа Ф.
Согласно ф-ле (6), при
Т=0 К Ф. в кристалле отсутствуют. При T<<QД
их число NФ пропорц. T3, а при T<<QД
линейно растёт с температурой:
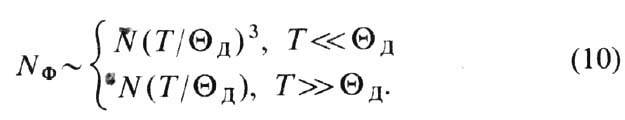
Здесь N-число ячеек
кристалла. Из соотношений (10) видно, что даже при сверхнизких темп-pax (Т~
1 К) число Ф. в 1 см3 огромно (при 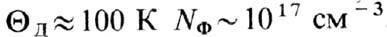 ; при
; при 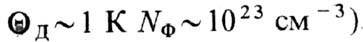 , При T>>QД число Ф. превышает число ячеек кристалла
N. При T<<QД практически все Ф. являются акустическими,
число оптич. Ф. экспоненциально мало. Неидеальность газа Ф. тем меньше, чем
ниже температура.
, При T>>QД число Ф. превышает число ячеек кристалла
N. При T<<QД практически все Ф. являются акустическими,
число оптич. Ф. экспоненциально мало. Неидеальность газа Ф. тем меньше, чем
ниже температура.
При Т>= 300 К
в газе Ф. содержится большая часть тепловой энергии кристалла. Гармонич. представление
достаточно для объяснения Дюлонга и Пти закона ,к-рый является следствием
линейного роста числа Ф. с повышением температуры. В твёрдых телах, где Ф.- единств.
квазичастицы, существующие при T<<QД, резкое
уменьшение их числа с падением температуры приводит к падению теплоёмкости.
Взаимодействия фононов. Ангармонизм колебаний означает существование взаимодействия между Ф., в
процессе к-рого Ф. могут возникать, аннигилировать и рассеиваться друг на друге
с изменением частоты и поляризации. При этом суммарные энергия и квазиимпульс
сохраняются (последний с точностью до вектора обратной решётки).
Взаимодействие между Ф.
позволяет объяснить тепловое расширение твёрдых тел, различие в величинах и
в температурном изменении уд. теплоёмкостей при пост. давлении (cР)и пост. объёме (сV), зависимость упругих постоянных (см.
Модули упругости) от температуры и давления.
Взаимодействие Ф.- осн.
механизм, посредством к-рого распределение Ф. может быть приведено в состояние
тер-модинамич. равновесия. Взаимодействие Ф. играет важную роль в определении
времени жизни Ф. t. Оно существенно зависит от температуры, резко уменьшаясь с повышением
Т, что приводит к возрастанию неидеальности газа Ф.
Ф. взаимодействуют не только
друг с другом, но и с др. квазичастицами: с электронами проводимости в
металлах и полупроводниках, с магнонами в магнитно-упорядоченных средах
(см. Спиновые волны ).Испускание и поглощение Ф. электронами - осн. механизм
электрич. сопротивления металлов и полупроводников (см. Рассеяние носителей
заряда, Электрон-фононное взаимодействие). Обмен электронов Ф. приводит
к притяжению электронов друг к другу и, в свою очередь, к образованию куперовских
пар (см. Купера эффект) - осн. носителей незатухающего сверхпроводящего
тока (см. Сверхпроводимость).
Взаимодействие магнонов
с Ф. (их рассеяние и взаимопревращение)- одна из причин релаксации магнитной.
Оно определяет ширины магн.
резонансов (см. Антиферромагнитный резонанс, Ферромагнитный резонанс); резонансное
взаимодействие между фононом и магноном - причина т.н. ф е р р о а к у с т и
ч е с к о г о р е з о н а н с а.
В релаксац. процессах в
твёрдых телах Ф. обычно служат "стоком" для энергии и квазиимпульса,
запасённых ансамблями др. квазичастиц (в частности, электронами). Ф. играют
роль внутр. термостата. Как правило, именно с помощью Ф. осуществляется связь
всех квазичастиц твёрдого тела с окружающей средой. Сравнительно слабая связь
Ф. с др. квазичастицами (с электронами, магнонами) может привести к отрыву температуры
последних (напр., электронной температуры) от температуры кристаллич. решётки, т.е.
газа Ф. (см., напр., Горячие электроны).
Ф. упруго рассеиваются
на дефектах кристаллич. решётки (вакансиях ,междоузлиях, дислокациях, границах кристаллов, границах образца).
Плотность состояний
фононов. Для описания термодина-мич. свойств кристалла в гармонич. приближении
достаточно знать число состояний Ф. в интервале энергий E, 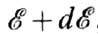 т. е. плотность состояний:
т. е. плотность состояний:
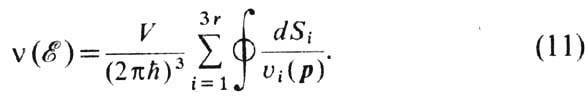
Здесь V-объём кристалла,
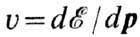 -скорость
Ф.; интегрирование ведётся по изоэнергетич. поверхности
-скорость
Ф.; интегрирование ведётся по изоэнергетич. поверхности 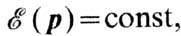 dS-элемент этой поверхности. Благодаря обращению в нек-рых точках импульсного
пространства скорости u в ноль плотность состояний имеет особенности
при нек-рых изолированных (критич.) значениях энергии
dS-элемент этой поверхности. Благодаря обращению в нек-рых точках импульсного
пространства скорости u в ноль плотность состояний имеет особенности
при нек-рых изолированных (критич.) значениях энергии 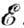 ,
в к-рых функция
,
в к-рых функция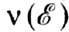 непрерывна, а её производные испытывают скачок (см. Ван Хова особенности).
непрерывна, а её производные испытывают скачок (см. Ван Хова особенности).
Непосредств. расчёт фононного
спектра - сложная задача, требующая подробного знания сил, действующих между
атомами (см. Межатомное взаимодействие). Определение 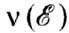 вносит дополнит. трудности. Поэтому обычно плотность состояний моделируют простыми
функциями, соответствующими простейшим моделям колебаний кристаллич. решётки -
Дебая
(см. Дебая теория).
вносит дополнит. трудности. Поэтому обычно плотность состояний моделируют простыми
функциями, соответствующими простейшим моделям колебаний кристаллич. решётки -
Дебая
(см. Дебая теория).
Экспериментальные методы определения закона дисперсии Ф. 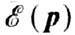 основаны на взаимодействии Ф. с нейтральными частицами (фотонами и нейтронами).
Поглощение ИК-фотонов кристаллами, как правило, означает резонансное превращение
фотона в оптич. Ф. Т. к. импульс фотона очень мал, то по поглощению ИК-фотонов
можно определить энергию оптич. Ф. с импульсом, близким к нолю. Неупругое рассеяние
световых фотонов (см. Мандельштама- Бриллюэна рассеяние), как и неупругое
рассеяние нейтронов в кристаллах, связано с рождением и поглощением Ф.
основаны на взаимодействии Ф. с нейтральными частицами (фотонами и нейтронами).
Поглощение ИК-фотонов кристаллами, как правило, означает резонансное превращение
фотона в оптич. Ф. Т. к. импульс фотона очень мал, то по поглощению ИК-фотонов
можно определить энергию оптич. Ф. с импульсом, близким к нолю. Неупругое рассеяние
световых фотонов (см. Мандельштама- Бриллюэна рассеяние), как и неупругое
рассеяние нейтронов в кристаллах, связано с рождением и поглощением Ф.
Определению законов дисперсии
акустич. Ф. способствует явление фокусировки фононов (см. также Баллистические
фононы).
Заключение. Концепция
Ф. (как и др. квазичастиц) помогает описать мн. свойства твёрдых тел, используя
представления кинетич. теории газов. Так, решёточная теплопроводность кристаллов
для неметаллов-это теплопроводность газа Ф., длина свободного пробега к-рых
ограничена фонон-фононным взаимодействием, а также дефектами кристаллич. решётки
при низких темп-pax (границами образца). Поглощение звука в кристаллич.
диэлектриках- результат взаимодействия звуковой волны с тепловыми Ф. В аморфных
(в т. ч. стеклообразных) телах Ф. удаётся ввести только для длинноволновых акустич.
колебаний, мало чувствительных к взаимному расположению атомов и допускающих
континуальное описание твёрдого тела (см. Упругости теория).
Ф. наз. также квазичастицы, соответствующие элементарным возбуждениям в сверхтекучем гелии, описывающие колебат. движение квантовой жидкости (см. Сверхтекучесть ).Ф. в Не характеризуются импульсом (а не квазиимпульсом), т.к. они описывают возбуждённое состояние однородной изотропной среды (см. также Ротон).

М. И. Каганов
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|