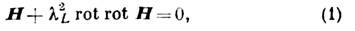
Лондонов уравнение - феноменологии, ур-ние, описывающее распределение магн. поля в сверхпроводниках.
Предложено Ф. Лондоном и X. Лондоном (F. London, H. London, 1935) задолго до
построения микроскопич. теории сверхпроводимости (1957, см. Бардина - Купера
- Шриффера модель). Л. у. имеет вид
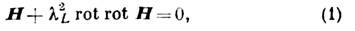
где Н - локальное
магн. поле в сверхпроводнике, 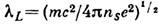 - параметр, имеющий размерность длины и наз. лондоновской глубиной (см. Глубина
проникновения)проникновения магн. поля. Здесь т и е - соответственно
масса и заряд электрона, ns - концентрация сверхпроводящих
электронов, т. е. электронов, объединённых в куперовские пары (см. Купера
эффект). Ур-ние (1) получается в результате минимизации свободной энергии
сверхпроводника F-
- параметр, имеющий размерность длины и наз. лондоновской глубиной (см. Глубина
проникновения)проникновения магн. поля. Здесь т и е - соответственно
масса и заряд электрона, ns - концентрация сверхпроводящих
электронов, т. е. электронов, объединённых в куперовские пары (см. Купера
эффект). Ур-ние (1) получается в результате минимизации свободной энергии
сверхпроводника F-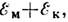 состоящей из энергии
магн. поля
состоящей из энергии
магн. поля 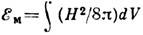 и кинетич. энергии сверхпроводящих электронов движущихся
в сверхпроводнике с
и кинетич. энергии сверхпроводящих электронов движущихся
в сверхпроводнике с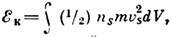 постоянной по времени скоростью vs при наличии в нём бездиссипативного
электрич. тока
постоянной по времени скоростью vs при наличии в нём бездиссипативного
электрич. тока

Вариация свободной энергии
по Н с учётом Максвелла уравнения rot Н=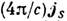 даёт ур-ние (1). Л. у. (1) описывает Мейснера эффект ,т. е. спадание
магн. поля в глубь сверхпроводника. Так, на глубине z под плоской поверхностью
сверхпроводника, согласно ур-нию
даёт ур-ние (1). Л. у. (1) описывает Мейснера эффект ,т. е. спадание
магн. поля в глубь сверхпроводника. Так, на глубине z под плоской поверхностью
сверхпроводника, согласно ур-нию
(1), H(z)
= H(0) ехр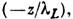 где H(0) - напряжённость поля на поверхности. Т. о., магн. поле проникает
в сверхпроводник лишь на глубину
где H(0) - напряжённость поля на поверхности. Т. о., магн. поле проникает
в сверхпроводник лишь на глубину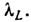 Для металлов
Для металлов 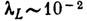 мкм.
мкм.
Ур-ние (1) предполагает
наличие локальной связи (2)
между током и скоростью сверхпроводящих электронов: ток в нек-рой точке сверхпроводника
зависит от скорости сверхпроводящих электронов в той же точке. Это имеет место,
когда глубина проникновения 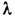 значительно больше длины когерентности
значительно больше длины когерентности 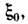 определяющей расстояние, на к-ром скоррелированы волновые функции сверхпроводящих
электронов. Сверхпроводники, у к-рых
определяющей расстояние, на к-ром скоррелированы волновые функции сверхпроводящих
электронов. Сверхпроводники, у к-рых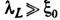 и к к-рым, следовательно, применимо ур-ние (1), наз. лондоновскими сверхпроводниками.
В случае малой глубины проникновения локальная связь (2) нарушается. Для описания
эффекта Мейснера в таких сверхпроводниках А. Б. Пипнардом (А. В. Pippard, 1953)
было предложено нелокальное обобщение ур-ния (1). Сверхпроводники с
и к к-рым, следовательно, применимо ур-ние (1), наз. лондоновскими сверхпроводниками.
В случае малой глубины проникновения локальная связь (2) нарушается. Для описания
эффекта Мейснера в таких сверхпроводниках А. Б. Пипнардом (А. В. Pippard, 1953)
было предложено нелокальное обобщение ур-ния (1). Сверхпроводники с 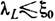 наз. пиппардовскими; к ним относятся
сверхпроводники 1-го рода при темп-pax, не очень близких к критич. температуре.
К лондоновским относятся сверхпроводники 2-го рода (как правило, сплавы), а
также сверхпроводники при температуре, близкой к критической. В последнем случае
ур-ние (1) является следствием феноменологич. теории сверхпроводимости
и может быть выведено на основании микроскопич. теории (Л. П. Горьков, 1959).
наз. пиппардовскими; к ним относятся
сверхпроводники 1-го рода при темп-pax, не очень близких к критич. температуре.
К лондоновским относятся сверхпроводники 2-го рода (как правило, сплавы), а
также сверхпроводники при температуре, близкой к критической. В последнем случае
ур-ние (1) является следствием феноменологич. теории сверхпроводимости
и может быть выведено на основании микроскопич. теории (Л. П. Горьков, 1959).

Н. Б. Копнин
|
|