 Математическим аппаратом теории Максвелла послужил векторный анализ, представленный
в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал,
что его заслуга состоит лишь в математическом оформлении идей Фарадея.
Математическим аппаратом теории Максвелла послужил векторный анализ, представленный
в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал,
что его заслуга состоит лишь в математическом оформлении идей Фарадея. Установлению уравнений Максвелла предшествовал ряд открытий законов
взаимодействий заряженных, намагниченных и токонесущих тел (в частности,
законов Кулона, Био - Савара, Ампера). В 1831 M. Фарадей (M. Faraday) открыл
закон электромагнитной индукции и примерно в то же время ввёл понятие электрического и магнитного
полей как самостоятельных физических субстанций. Опираясь на фарадеевское представление
о поле и введя ток смещения, равнозначный по своему магнитному действию обычному
электрическому току, Дж. К. Максвелл (J. С. Maxwell, 1864) сформулировал систему
уравнений, названную впоследствии уравнениями Максвелла. Уравнения Максвелла функционально связывают
электрического и магнитного поля с зарядами и токами и охватывают собой все известные
закономерности макроэлектромагнетизма. Впервые об уравнениях Максвелла было доложено на заседании
Лондонского Королевского общества 27 октяьря 1834 года. Первоначально Максвелл прибегал
к вспомогательным механическим моделям Эфира, но уже в "Трактате
об электричестве и магнетизме" (1873) электромагнитное поле рассматривалось как
самостоятельный физический объект. Физическая основа уравнений Максвелла - принцип близкодействия, утверждающий,
что передача электромагнитных возмущений от точки к точке происходит с конечной скоростью
(в вакууме со скоростью света с). Он противопоставлялся ньютоновскому принципу
дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние Математическим аппаратом теории Максвелла послужил векторный анализ, представленный
в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал,
что его заслуга состоит лишь в математическом оформлении идей Фарадея.
Математическим аппаратом теории Максвелла послужил векторный анализ, представленный
в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал,
что его заслуга состоит лишь в математическом оформлении идей Фарадея.
Каноническая форма записи, принятая ныне, принадлежит
Г. Герцу (H. Hertz) и О. Хевисайду (О. Heaviside) и основана на использовании
не кватернионных, а векторных полей: напряжённости электрического поля E,
напряжённости магнитного поля H, векторов электрической индукции
D и магнитной индукции В.
уравнения Максвелла связывают их между
собой, с плотностью электрического заряда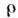 и плотностью электрического тока J, которые рассматриваются как источники:
и плотностью электрического тока J, которые рассматриваются как источники:
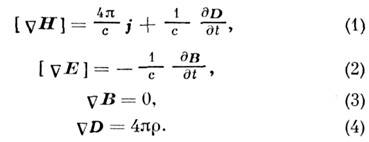
Здесь использована Гаусса система единиц (о
записи уравнений Максвелла в др. системах см. в разделе 15). Входящие в (1) - (4) величины
E, D, j являются истинными, или полярными,
векторами (а величина r - истинным скаляром), поля H и В - псевдовекторами,
или аксиальными векторами. Все эти величины предполагаются непрерывными
(вместе со всеми производными) функциями времени t и координат 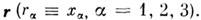 Следовательно, в уравнениях (1) - (4) не учитывается
ни дискретная структура электрических зарядов и токов, ни квантовый характер самих
полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом
(классич.) приближении с помощью Лоренца - Максвелла уравнений.
Следовательно, в уравнениях (1) - (4) не учитывается
ни дискретная структура электрических зарядов и токов, ни квантовый характер самих
полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом
(классич.) приближении с помощью Лоренца - Максвелла уравнений.
Используя Гаусса - Остроградского формулу и С такса формулу, уравнениям (1) - (4) можно придать форму интегральных:
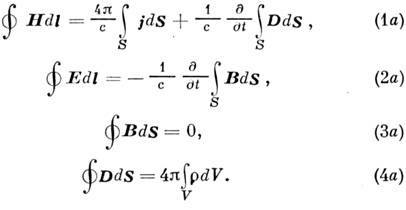
Криволинейные интегралы в (1a), (2a)
берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных
полей), а стоящие в правых частях поверхностные интегралы - по поверхностям,
ограниченным этими контурами (опирающимся на них), причём направление циркуляции
(направление элемента контура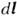 )
связано с направлением нормали к S (вектор
)
связано с направлением нормали к S (вектор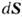 )
правовинтовым соотношением (если в качестве исходного выбрано пространство с
правыми системами координат). В интегралах по замкнутым поверхностям (S)
в (3а), (4а) направление вектора элемента площади
)
правовинтовым соотношением (если в качестве исходного выбрано пространство с
правыми системами координат). В интегралах по замкнутым поверхностям (S)
в (3а), (4а) направление вектора элемента площади 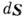 совпадает с наружной нормалью к поверхности; V - объём, ограниченный
замкнутой поверхностью S.
совпадает с наружной нормалью к поверхности; V - объём, ограниченный
замкнутой поверхностью S.
Уравнения Максвелла в форме (1a) - (4a) предназначаются
не только для изучения топологич. свойств электромагнитных полей, но и являются удобным
аппаратом решения конкретных задач электродинамики в системах с достаточно высокой
симметрией или с априорно известными распределениями полей. Кроме того, в математическом отношении эта система уравнений содержательнее системы (1) - (4), поскольку пригодна
для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении
физ. пределов применимости обе системы уравнений равнозначны, т. к. любые скачки
полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно
плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения
уравнений Лоренца - Максвелла. С этими оговорками резкие скачки можно описывать
и в рамках уравнений Максвелла (1) - (4), прибегая к аппарату обобщённых функций.
Наконец, уравнения Максвелла в интегральной форме облегчают
физ. интерпретацию MH. электромагнитных явлений и поэтому нагляднее сопоставляются
с теми экспериментально установленными законами, которым они обязаны своим происхождением.
Так, уравнение (1a) есть обобщение Био - Савара закона (с
добавлением к току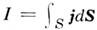 максвелловского смещения тока).
максвелловского смещения тока).
Уравнение (2a) выражает закон индукции Фарадея;
иногда его правую часть переобозначают через "магнитный ток смещения"
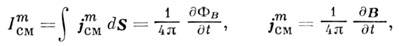
где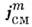 -
плотность "магнитного тока смещения", ФВ - магнитный поток.
Уравнение (За) связывают с именем Гаусса
-
плотность "магнитного тока смещения", ФВ - магнитный поток.
Уравнение (За) связывают с именем Гаусса  , установившим соленоидальность поля В, обусловленную отсутствием истинных
магнитных зарядов. Впрочем вопрос о существовании магнитных монополей пока
остаётся открытым. Но соответствующее обобщение уравнений Максвелла произведено (Хевисайд,
1885) на основе принципа двойственной симметрии уравнений Максвелла (см. в разделе 9), для
чего в (2) и (2a) наряду с магнитным током смещения вводится ещё и "истинный"
магнитный ток (процедура, обратная проделанной когда-то Максвеллом с электрическим током
в первом уравнении), а в уравнение Гаусса (3), (За) - магнитный заряд
, установившим соленоидальность поля В, обусловленную отсутствием истинных
магнитных зарядов. Впрочем вопрос о существовании магнитных монополей пока
остаётся открытым. Но соответствующее обобщение уравнений Максвелла произведено (Хевисайд,
1885) на основе принципа двойственной симметрии уравнений Максвелла (см. в разделе 9), для
чего в (2) и (2a) наряду с магнитным током смещения вводится ещё и "истинный"
магнитный ток (процедура, обратная проделанной когда-то Максвеллом с электрическим током
в первом уравнении), а в уравнение Гаусса (3), (За) - магнитный заряд
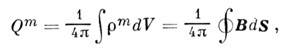
где 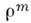 -
плотность магнитного заряда. Фактически все экспериментальные установки для регистрации
ожидаемых магнитных монополей основаны на этом предположении.
Наконец, уравнение (4a) определяет поле свободного электрического заряда; его
иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не
содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо
не только в электростатике, но и для систем с произвольным изменением поля во
времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера
(A. Ampere).
-
плотность магнитного заряда. Фактически все экспериментальные установки для регистрации
ожидаемых магнитных монополей основаны на этом предположении.
Наконец, уравнение (4a) определяет поле свободного электрического заряда; его
иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не
содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо
не только в электростатике, но и для систем с произвольным изменением поля во
времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера
(A. Ampere).
Совокупность уравнений Максвелла (1) - (4) составляет систему
из восьми (двух векторных и двух скалярных) линейных дифференц. уравнений 1-го
порядка для четырёх векторов 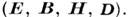 Источники (скаляр
Источники (скаляр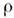 и
вектор
и
вектор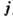 ) не могут
быть заданы произвольно; применяя операцию
) не могут
быть заданы произвольно; применяя операцию 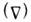 к
уравнению (1) и подставляя результат в (4), получаем:
к
уравнению (1) и подставляя результат в (4), получаем:

или в интегральной форме:
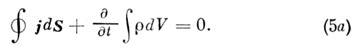
Это уравнение непрерывности для тока, содержащее
в себе закон сохранения заряда для замкнутых изолнров. областей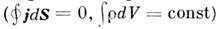 ,-
один из фундаментальных физических принципов, подтверждаемых в любых экспериментах.
,-
один из фундаментальных физических принципов, подтверждаемых в любых экспериментах.
Уравнения (1) - (4) распадаются на два самостоят,
"блока": уравнения (1) и (4), содержащие векторы 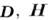 и
источники
и
источники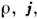 и
уравнения (2) и (3) - однородные уравнения для
и
уравнения (2) и (3) - однородные уравнения для 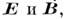 не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения,
в котором
не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения,
в котором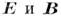 выражаются
через т. H. потенциалы электромагнитного поля
выражаются
через т. H. потенциалы электромагнитного поля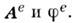 При
этом уравнение (3) "почти следует" из (2), т. к. операция (у), применённая
к (2), даёт
При
этом уравнение (3) "почти следует" из (2), т. к. операция (у), применённая
к (2), даёт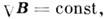 что отличается от (3) только константой, определяемой нач. условиями. Аналогично
уравнение (4) "почти следует" из (1) и уравнения непрерывности (5).
что отличается от (3) только константой, определяемой нач. условиями. Аналогично
уравнение (4) "почти следует" из (1) и уравнения непрерывности (5).
Система уравнений Максвелла (1) - (4) не является полной: по
существу, она связывает 4 векторные величины двумя векторными уравнениями. Её замыкание
осуществляется путём добавления соотношений, связывающих векторы 1-го "блока"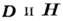 с
векторами 2-го "блока"
с
векторами 2-го "блока"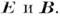 Эти соотношения зависят от свойств сред
(материальных сред), в которых происходят электромагнитные процессы, и называются материальными
уравнениями (см. раздел 7).
Эти соотношения зависят от свойств сред
(материальных сред), в которых происходят электромагнитные процессы, и называются материальными
уравнениями (см. раздел 7).
В силу линейности системы (1) - (4) для её решений
справедлив суперпозиции принцип .Часто оказывается удобным фурье-представление
общего решения (1) - (4) как функции времени (см. Фурье преобразование). Записывая
временной фактор в виде 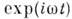 ,
для комплексных фурье-амплитуд
,
для комплексных фурье-амплитуд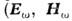 и
т. д.) получаем систему уравнений
и
т. д.) получаем систему уравнений
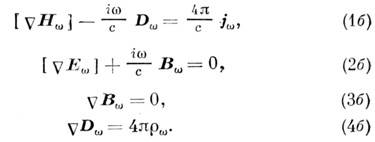
Система (1б) - (4б) в некотором смысле удобнее
(1) - (4), ибо упрощает применение к электродинамич. системам, обладающим временной
дисперсией (см. раздел 7), т. е. зависимостью параметров от частоты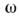
Если распространить (в силу линейности уравнений Максвелла)
фурье-разложение и на зависимость полей от пространственных координат, т. е.
представить общее решение уравнений (1) - (4) в виде суперпозиции плоских волн
типа 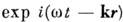 (k -
волновой вектор), то для фурье-компонентов
нолей
(k -
волновой вектор), то для фурье-компонентов
нолей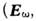 k и т.
д.) получим систему алгебраич. уравнений:
k и т.
д.) получим систему алгебраич. уравнений:
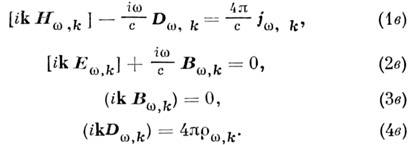
Такое сведение уравнений Максвелла к набору уравнений для осцилляторов
(осцилляторов поля) составляет важный этап перехода к квантовой электродинамике,
где электромагнитное поле рассматривается как совокупность фотонов, характеризуемых
энергиями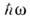 и импульсами
и импульсами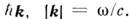 Однако и в макроэлектродинамике представления (1в) - (4в) оказываются
иногда вполне адекватными физ. сущности процессов: например, при выделении откликов
высокодобротных систем (см. Объёмный резонатор) или при изучении "механизма
формирования" мод со сложной пространственной структурой из набора плоских
волн и т. п. Наконец, уравнения Максвелла в форме (1в) - (4в) удобны для описания
свойств электродинамич. систем, обладающих не только временной, но и пространственной
дисперсией, если последняя задаётся в виде зависимости параметров от волнового
вектора k.
Однако и в макроэлектродинамике представления (1в) - (4в) оказываются
иногда вполне адекватными физ. сущности процессов: например, при выделении откликов
высокодобротных систем (см. Объёмный резонатор) или при изучении "механизма
формирования" мод со сложной пространственной структурой из набора плоских
волн и т. п. Наконец, уравнения Максвелла в форме (1в) - (4в) удобны для описания
свойств электродинамич. систем, обладающих не только временной, но и пространственной
дисперсией, если последняя задаётся в виде зависимости параметров от волнового
вектора k.
В макроэлектродинамике материальные связи, характеризующие
электромагнитные свойства сред, вводятся феноменологически; они находятся либо непосредственно
из эксперимента, либо на основании модельных представлений. Существуют два способа
описания: в одном векторы E и H считаются
исходными и материальные уравнения задаются в виде D = D(E
, H) и В = В( Е,Н), в
другом - за исходные берутся векторы 2-го "блока" E и В, и соответствующие материальные связи представляются иначе: D =
D(E,В), H= H(E, В). Оба описания совпадают для вакуума, где материальные уравнения вырождаются
в равенства D = E и B = H.
Рассмотрим простейшую модель среды, характеризуемую
мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и
H. Под действием поля E в такой среде возникает электрическая поляризация
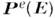 (см. Поляризации
вектор), а под действием поля H - магнитная поляризация
(см. Поляризации
вектор), а под действием поля H - магнитная поляризация 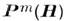 .
Чаще её наз. намагниченностью и обозначают М.
.
Чаще её наз. намагниченностью и обозначают М.
Материальные уравнения для таких сред имеют вид
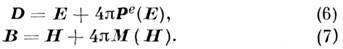
При этом индуцированные в среде электрические заряды
наз. связанными или поляризац. зарядами с плотностью 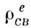 , а токи, обусловленные их изменениями,- поляризац. токами с плотностью
, а токи, обусловленные их изменениями,- поляризац. токами с плотностью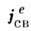 :
:
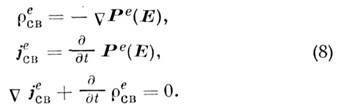
Эти понятия были перенесены и на магнитные поля,
что можно выразить в виде системы уравнений, аналогичной
(8):
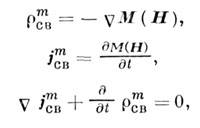
и только потом выяснилось, что истинными источниками намагничивания
среды оказались электрические токи 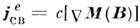 ,
а не магнитные заряды. Поэтому терминология сложилась на основе физически некорректной
системы
,
а не магнитные заряды. Поэтому терминология сложилась на основе физически некорректной
системы
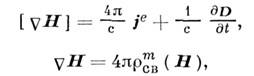
тогда как следовало бы принять беззарядовые уравнения
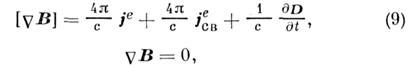
что равносильно замыканию исходных уравнений Максвелла (1)
- (4) с помощью материальных связей
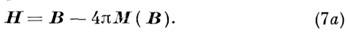
Из (6) и (7a) следует, что 2-й вариант представления
материальных соотношений, в котором постулируются в качестве исходных векторы
E и B, физически предпочтительнее.
В модели Лоренца - Максвелла усреднение микрополя
Нмикро, произведённое с учётом вклада со стороны индуциров. полей,
приводит к уравнениям (9) и соответственно <Нмикро>= В.
Однако обычно параметры сред вводятся с помощью уравнений (7), что облегчает двойственную
симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости
сред (ce, cm) определяются соотношениями
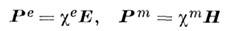
и позволяют
ввести диэлектрическую проницаемость e и магнитную проницаемость m:
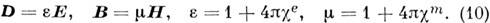
Простейшие модели сред характеризуются пост,
значениями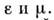 В
случае вакуума
В
случае вакуума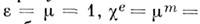 0.
0.
Классификация разл. сред ооычно основывается
на материальных уравнениях типа (10) и их обобщениях. Если проницаемости e
и m не зависят от полей, то уравнения Максвелла (1) - (4) вместе с материальными уравнениями
(10) остаются линейными, поэтому о таких средах говорят как о линейных средах.
При наличии зависимостей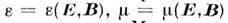 среды
наз. нелинейными: решения уравнений Максвелла в нелинейных средах не удовлетворяют
принципу суперпозиции. Если проницаемости зависят от координат
среды
наз. нелинейными: решения уравнений Максвелла в нелинейных средах не удовлетворяют
принципу суперпозиции. Если проницаемости зависят от координат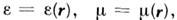 то говорят о неоднородных средах, при зависимости
от времени
то говорят о неоднородных средах, при зависимости
от времени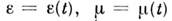 - о нестац попарных средах (иногда такие
электродинамич. системы наз. параметрическими). Для анизотропных сред скаляры
e, m в (10) заменяются на тензоры:
- о нестац попарных средах (иногда такие
электродинамич. системы наз. параметрическими). Для анизотропных сред скаляры
e, m в (10) заменяются на тензоры: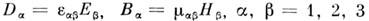 (по дважды встречающимся индексам производится
суммирование). Важное значение имеют также эффекты запаздывания и нелокальности
отклика среды на внеш. поля.
(по дважды встречающимся индексам производится
суммирование). Важное значение имеют также эффекты запаздывания и нелокальности
отклика среды на внеш. поля.
Значение индуциров. поляризации Ре, напр, в момент г, может определяться, вообще говоря, значениями полей
во все предыдущие моменты времени, т. е.
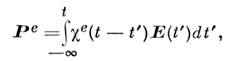
что при преобразовании Фурье по времени приводит
к зависимости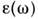 [соответственно
[соответственно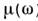 i].
Такие среды наз. средами с временной (частотной)
дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается
и для нелокальных взаимодействий, когда отклик в точке г зависит от значения
полей, строго говоря, во всех окружающих
точках
i].
Такие среды наз. средами с временной (частотной)
дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается
и для нелокальных взаимодействий, когда отклик в точке г зависит от значения
полей, строго говоря, во всех окружающих
точках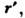 но обычно
всё-таки в пределах некоторой конечной её окрестности:
но обычно
всё-таки в пределах некоторой конечной её окрестности: 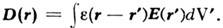 При преобразовании Фурье по г это приводит к появлению зависимостей
При преобразовании Фурье по г это приводит к появлению зависимостей 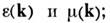 такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).
такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).
В проводящих средах входящая в уравнений Максвелла (1) - (5)
плотность тока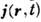 состоит из двух слагаемых: одно по-прежнему
является сторонним током
состоит из двух слагаемых: одно по-прежнему
является сторонним током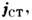 обусловленным
заданным перемещением электрических зарядов под действием сторонних сил (обычно
неэлектрического происхождения), а другое - током проводимости
обусловленным
заданным перемещением электрических зарядов под действием сторонних сил (обычно
неэлектрического происхождения), а другое - током проводимости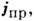 зависящим
от полей, определяемых системой уравнений Максвелла, и связанным с ними материальными уравнениями
вида
зависящим
от полей, определяемых системой уравнений Максвелла, и связанным с ними материальными уравнениями
вида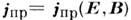 В простейшем
случае эта зависимость сводится к локальному Ома закону,
В простейшем
случае эта зависимость сводится к локальному Ома закону,
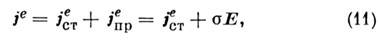
где 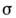 -
электропроводность (проводимость) среды. Иногда в (11) вводят обозначение
-
электропроводность (проводимость) среды. Иногда в (11) вводят обозначение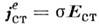 ,
благодаря которому различают системы с заданными
токами и системы с заданными полями (напряжениями). Для синусоидальных во времени
полей, подчинённых уравнениям (1б) - (4б) и материальным связям (10) и (11), вводится
комплексная диэлектрическая проницаемость, объединяющая (10) и (11),
,
благодаря которому различают системы с заданными
токами и системы с заданными полями (напряжениями). Для синусоидальных во времени
полей, подчинённых уравнениям (1б) - (4б) и материальным связям (10) и (11), вводится
комплексная диэлектрическая проницаемость, объединяющая (10) и (11),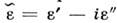 ,
мнимая часть которой обусловлена проводимостью и определяет
диссипацию энергии
электромагнитного поля в среде. По аналогии вводится комплексная магнитная
проницаемость
,
мнимая часть которой обусловлена проводимостью и определяет
диссипацию энергии
электромагнитного поля в среде. По аналогии вводится комплексная магнитная
проницаемость 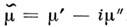 , мнимая
часть которой обусловливает потери, связанные с перемагничиванием среды.
Комплексные проницаемости в общем случае зависят от частоты w и волнового
вектора
, мнимая
часть которой обусловливает потери, связанные с перемагничиванием среды.
Комплексные проницаемости в общем случае зависят от частоты w и волнового
вектора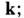 эти зависимости
не могут быть произвольными: причинности принцип связывает их действительные
и мнимые части Крамерса - Кронига соотношениями.
эти зависимости
не могут быть произвольными: причинности принцип связывает их действительные
и мнимые части Крамерса - Кронига соотношениями.
В общем случае вид материальных уравнений зависит
также и от системы отсчёта, в которой эти уравнения рассматривают. Так, если в неподвижной
системе К среда характеризуется простейшими уравнениями (10), то в инер-циальной
системе К' , движущейся относительно К с пост, скоростью и, появляется
анизотропия:
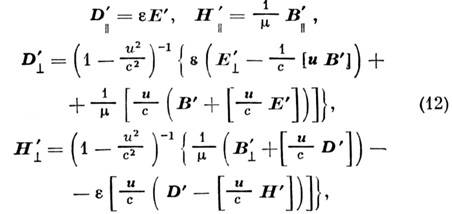
где индексы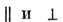 обозначают
продольные и поперечные к
обозначают
продольные и поперечные к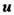 составляющие
векторов. В рамках алгебраических уравнений Максвелла (1в) - (4в) материальные уравнения (12) могут
быть переписаны в виде
составляющие
векторов. В рамках алгебраических уравнений Максвелла (1в) - (4в) материальные уравнения (12) могут
быть переписаны в виде
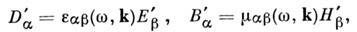
что можно трактовать как наличие временной и
пространственной дисперсии. Исследование процессов с материальными связями типа
(12) составляет предмет электродинамики движущихся сред. Заметим, что
хотя характеристики е и m удобно симметризуют материальные уравнения, их введение
не является непременным условием замыкания уравнений Максвелла. Соответствующей перенормировкой
допустимо свести описание магнитного поля к одновекторному, т. е. сделать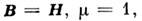 но при этом даже для изотропной среды диэлектрическая проницаемость становится тензором, она различна для вихревых и потенциальных
полей. Физически это связано с неоднозначностью модельного представления диполь-ных
моментов, во всяком случае при
но при этом даже для изотропной среды диэлектрическая проницаемость становится тензором, она различна для вихревых и потенциальных
полей. Физически это связано с неоднозначностью модельного представления диполь-ных
моментов, во всяком случае при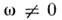 они
могут равноправно интерпретироваться и как
зарядовые, и как токовые.
они
могут равноправно интерпретироваться и как
зарядовые, и как токовые.
Поскольку уравнения Максвелла справедливы для любых (в рамках
применимости макроэлектродинамики) неоднородных сред, то в областях резкого
изменения их параметров иногда можно игнорировать тонкую структуру распределения
полей в переходном слое и ограничиться "сшиванием" полей по разные
стороны от него, заменяя тем самым переходный слой математической поверхностью - границей,
лишённой толщины. Если внутри переходной области имелись заряды с объёмной плотностью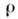 или
токи с объёмной плотностью
или
токи с объёмной плотностью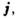 то
при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся
поверхностные заряды rпов
и поверхностные токи
то
при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся
поверхностные заряды rпов
и поверхностные токи
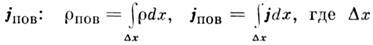 -
толщина переходного слоя.
-
толщина переходного слоя.
Применение уравнений Максвелла и уравнения непрерывности приводит
к следующим граничным условиям:
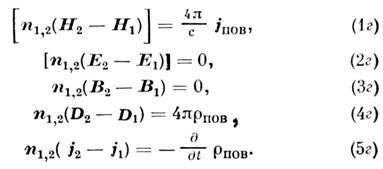
Здесь индексы 1 и 2 характеризуют поля по разные
стороны от границы, а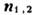 -
единичный вектор нормали к поверхности, направленный из среды 1 в среду 2.
Правила (1г) - (5г) пригодны для перехода через любые поверхности,
независимо от того, совпадают ли они с границами раздела сред или проходят по
однородным областям, поэтому их иногда наз. поверхностными уравнениями Максвелла.
-
единичный вектор нормали к поверхности, направленный из среды 1 в среду 2.
Правила (1г) - (5г) пригодны для перехода через любые поверхности,
независимо от того, совпадают ли они с границами раздела сред или проходят по
однородным областям, поэтому их иногда наз. поверхностными уравнениями Максвелла.
Иногда граничные условия (1г) - (5г)
порождают краевые условия, т. е. задают не правила перехода через границу, а
сами поля на ней. Напр., внутри идеального проводника 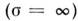 в силу (11)
в силу (11) 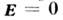 (иначе возник бы ток неограниченной плотности),
поэтому на границе раздела диэлектрик - идеальный проводник в согласии с (2г)
(иначе возник бы ток неограниченной плотности),
поэтому на границе раздела диэлектрик - идеальный проводник в согласии с (2г)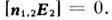 Такие
границы называются идеальными электрическими стенками.
Аналогично вводится понятие идеальной магнитной стенки, на которой
Такие
границы называются идеальными электрическими стенками.
Аналогично вводится понятие идеальной магнитной стенки, на которой 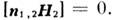 Если структура полей по одну сторону от границы универсальна, т. е. не зависит
от распределения полей по др. сторону, то краевые условия могут состоять в задании
не самих полей, а лишь связей между ними, например
Если структура полей по одну сторону от границы универсальна, т. е. не зависит
от распределения полей по др. сторону, то краевые условия могут состоять в задании
не самих полей, а лишь связей между ними, например 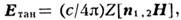 где Z - некоторая скалярная или тензорная
функция координат границы (
где Z - некоторая скалярная или тензорная
функция координат границы (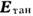 -
тангенциальный компонент
-
тангенциальный компонент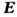 ).
К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.
).
К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.
Двойственная симметрия уравнений Максвелла имеет место для любой формы их записи.
Она состоит в инвариантности уравнений Максвелла относительно линейных
преобразований нолей, производимых по след, правилам:
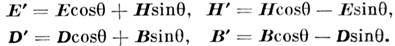
Здесь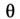 -
произвольный угл. параметр; в частности, при
-
произвольный угл. параметр; в частности, при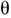 =
О получаются тождественные преобразования, а при
=
О получаются тождественные преобразования, а при 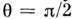 -
стандартные преобразования перестановочной
двойственности (операция
-
стандартные преобразования перестановочной
двойственности (операция 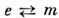 ):
замена
):
замена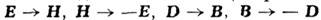 даёт в областях, свободных от источников,
новое решение уравнений Максвелла. При этом, однако, оно меняет местами уравнения
даёт в областях, свободных от источников,
новое решение уравнений Максвелла. При этом, однако, оно меняет местами уравнения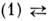
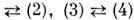 и, следовательно, там, где раньше были распределены электрические источники, возникают
источники магнитные
и, следовательно, там, где раньше были распределены электрические источники, возникают
источники магнитные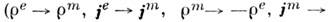
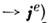 . Поэтому с точки зрения двойственной симметрии уравнений Максвелла задание материальных связей
в виде
. Поэтому с точки зрения двойственной симметрии уравнений Максвелла задание материальных связей
в виде 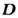
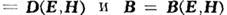 представляется вполне удобным. Дуально-симметричные уравнения Максвелла обладают рядом достоинств,
по крайней мере в чисто методич. плане. Так, например, они симметризуют скачки
тангенциальных компонентов магнитного и электрического полей и, если задание ffTall
на поверхности идеальной электрической стенки эквивалентно заданию поверхностного
электрического тока, то задание Я1а„ на идеальной магнитной стенке сводится
к заданию магнитного поверхностного тока:
представляется вполне удобным. Дуально-симметричные уравнения Максвелла обладают рядом достоинств,
по крайней мере в чисто методич. плане. Так, например, они симметризуют скачки
тангенциальных компонентов магнитного и электрического полей и, если задание ffTall
на поверхности идеальной электрической стенки эквивалентно заданию поверхностного
электрического тока, то задание Я1а„ на идеальной магнитной стенке сводится
к заданию магнитного поверхностного тока:
Таким сведением задач с заданными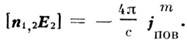 полями
к задачам с заданными токами широко пользуются в теории дифракции волн, в частности
в дифракции радиоволн.
полями
к задачам с заданными токами широко пользуются в теории дифракции волн, в частности
в дифракции радиоволн.
Принцип перестановочной двойственности является
представителем класса дискретных преобразований (см. Симметрия ),оставляющих
инвариантными уравнениями Максвелла. Такого же сорта преобразованиями являются, в частности,
операция обращения времени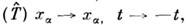
любые
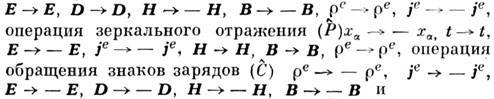
последовательно осуществляемые комбинации операций
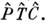
Различают теоремы единственности для стационарных
и нестационарных процессов. Условия единственности нестационарных решений извлекаются
из Пойн-тинга теоремы, где источники считаются заданными функциями координат
и времени. Если бы они порождали два разл. поля, то разность этих полей в вакууме
(или в любой линейной материальной среде)
вследствие принципа суперпозиции была бы решением однородных уравнений Максвелла. Для обращения
этой разности в нуль и, следовательно, получения единств, решения достаточно
удовлетворить след, трём условиям. 1) На поверхности S, окружающей область
V, где ищется поле, должны быть заданы тангенциальные составляющие поля
Етан или поля Нтан либо соотношения
между ними импедансного типа: 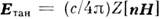 (п - нормаль к S) со значениями
Z, исключающими приток энергии извне. К таковым относятся, в частности, условия
излучения (см. Зоммерфельда условия излучения ),которым удовлетворяют волны
в однородной среде на больших расстояниях от источников. Во всех случаях поток
энергии для разностного поля вообще исчезает или направлен наружу (из объёма).
2) В нач. момент времени должны быть заданы все поля всюду внутри V. 3)
Плотность энергии электромагнитного поля
(п - нормаль к S) со значениями
Z, исключающими приток энергии извне. К таковым относятся, в частности, условия
излучения (см. Зоммерфельда условия излучения ),которым удовлетворяют волны
в однородной среде на больших расстояниях от источников. Во всех случаях поток
энергии для разностного поля вообще исчезает или направлен наружу (из объёма).
2) В нач. момент времени должны быть заданы все поля всюду внутри V. 3)
Плотность энергии электромагнитного поля 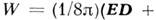 HB) должна быть положительна (вакуум, среды с
HB) должна быть положительна (вакуум, среды с 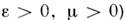 .
Эта частная теорема единственности обобщается
на среды с нелокальными связями, а также на некоторые виды параметрич. сред. Однако
в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений
о единственности не существует.
.
Эта частная теорема единственности обобщается
на среды с нелокальными связями, а также на некоторые виды параметрич. сред. Однако
в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений
о единственности не существует.
В стационарных режимах нач. условия выпадают,
и теоремы единственности формулируются непосредственно для установившихся решений.
Так, в электростатике достаточно задать все источники reст,
все полные заряды на изолиров. проводниках или их потенциалы, чтобы при соответствующих
условиях на бесконечности (нужное спадание поля) решение было бы единственным.
Аналогичные теоремы устанавливаются для магнитостатики и электродинамики пост,
токов в проводящих средах.
Особо выделяется случай синусоидальных во времени
процессов, для которых формулируют след, признаки, достаточные для получения единств,
решения: 1) задание источников 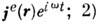 задание Eтан или Нтан на ограничивающей
объём V поверхности S или соответствующих импедансных условий,
обеспечивающих отсутствие потока вектора Пойнтинга внутрь V; 3) наличие
малого поглощения внутри V или малой утечки энергии через S для
исключения существования собств. колебаний на частоте
задание Eтан или Нтан на ограничивающей
объём V поверхности S или соответствующих импедансных условий,
обеспечивающих отсутствие потока вектора Пойнтинга внутрь V; 3) наличие
малого поглощения внутри V или малой утечки энергии через S для
исключения существования собств. колебаний на частоте 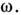
Классификация приближений уравнений Максвелла обычно основывается
на безразмерных параметрах, определяющих и критерии подобия для электромагнитных полей.
В вакууме таким параметром является отношение 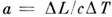 ,
где
,
где 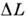 -
характерный масштаб изменения полей (либо размер области, в которой ищется решение),
-
характерный масштаб изменения полей (либо размер области, в которой ищется решение),
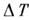 - характерный
временной масштаб изменения полей.
- характерный
временной масштаб изменения полей.
а) а = 0 - статич. приближение, статика.
Система уравнений Максвелла распадается на три.
I.
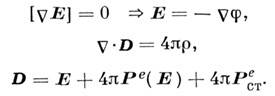
Материальная связь в простейшем случае имеет
вид 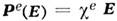 . Это система
уравнений Максвелла для электростатики, в которой источниками служат заданные распределения
плотности электрического заряда
. Это система
уравнений Максвелла для электростатики, в которой источниками служат заданные распределения
плотности электрического заряда 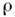 и сторонней поляризации
и сторонней поляризации 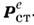 .
В однородной среде
.
В однородной среде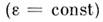 эл--статич. потенциал f определяется Пуассона уравнением
эл--статич. потенциал f определяется Пуассона уравнением
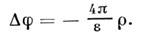
Для более сложных материальных <уравнений различают
электростатику анизотропных сред 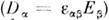 ,
нелинейную электростатику
,
нелинейную электростатику 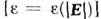 ,
электростатику сред с пространственной дисперсией
,
электростатику сред с пространственной дисперсией
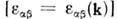 , важным
частным случаем которых являются движущиеся среды с временной дисперсией (здесь
может даже меняться тип уравнения для потенциала с эллиптического на параболический)
и т. п.
, важным
частным случаем которых являются движущиеся среды с временной дисперсией (здесь
может даже меняться тип уравнения для потенциала с эллиптического на параболический)
и т. п.
II. Поля в магнитостатике описываются уравнениями
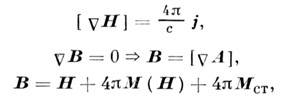
где в случае простейшей материальной связи индуци-ров.
намагниченность определяется соотношением
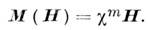
Источниками в уравнениях магнитостатики являются
заданные распределения плотности электрического тока 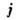 и сторонней намагниченности
и сторонней намагниченности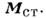 В однородной среде
В однородной среде
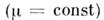 векторный потенциал магнитного поля
векторный потенциал магнитного поля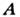 (калибровка
кулоновская) определяется векторным уравнением Пуассона
(калибровка
кулоновская) определяется векторным уравнением Пуассона
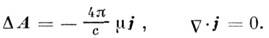
В общем случае возможны такие же разновидности
сред, что и в электростатике.
III. K статич. электродинамике относят и процессы
протекания пост, токов в распределённых проводящих средах. Токовая статика охватывается
уравнениями
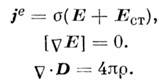
Источниками являются силы неэлектрического происхождения,
действующие на заряды, характеризующиеся напряжённостью 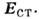 Электрические заряды присутствуют лишь в местах неоднородности среды, напр, на границах
проводящих сред. Распределение токов в проводящих средах сопоставимо с распределением
электрического и магнитного полей в электростатике и магнитостатике. Часто благодаря этой
аналогии говорят, например, о магнитных цепях, по которым "текут" магнитные потоки
Электрические заряды присутствуют лишь в местах неоднородности среды, напр, на границах
проводящих сред. Распределение токов в проводящих средах сопоставимо с распределением
электрического и магнитного полей в электростатике и магнитостатике. Часто благодаря этой
аналогии говорят, например, о магнитных цепях, по которым "текут" магнитные потоки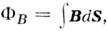 аналогичные электрическим токам
аналогичные электрическим токам 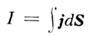 в
электрических цепях.
в
электрических цепях.
б) 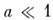 - квазистатика, обобщающая соответствующие статич. приближения.
- квазистатика, обобщающая соответствующие статич. приближения.
В квазиэлектростатике вакуумные электрические поля описываются уравнениями
статики (I.), а в уравнениях для магнитного поля в качество заданного
источника фигурирует и ток смещения. Квазимагнитостатика описывается статич.
уравнениями для магнитных полей с учётом закона индукции (2) для электрического поля. Поскольку
вихревое электрическое поле меняет электрические токи в проводниках, являющиеся источниками
магнитного поля, то этот раздел квазистатики более богат, чем предыдущий; он описывает
широкий круг явлений, происходящих в цепях перем, тока с сосредоточенными параметрами:
ёмкостями, индуктивностями и сопротивлениями.
Квазистатика в распределённых проводящих средах
описывается уравнениями квазистационарного (квазистатического) приближения, в которых током смещения пренебрегают по сравнению с токами проводимости.
В этом приближении распределения электрических токов, электрического и магнитного полей описываются
одинаковыми уравнениями диффузионного типа:
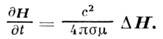
Эти уравнения определяют, например, распределение токов Фуко, проникновение переменного электромагнитного поля в проводник (скин-эффект) и т. п.
в) 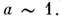 Резонансные волновые поля описываются точной системой уравнений Максвелла, однако их иногда
выделяют из общего класса полей, особенно в тех случаях, когда их структура
(пространственное распределение) фиксируется границами области, внутри которой
эти поля могут быть возбуждены (например, внутри полых резонаторов с металлическими
стенками или в поперечном сечении волноводов либо в окрестности тонкой проволочной
или щелевой антенны). При этом обычно обращаются к фурье-преобразованию уравнений Максвелла
и представлению поля в виде набора дискретных или квазидискретных мод.
Резонансные волновые поля описываются точной системой уравнений Максвелла, однако их иногда
выделяют из общего класса полей, особенно в тех случаях, когда их структура
(пространственное распределение) фиксируется границами области, внутри которой
эти поля могут быть возбуждены (например, внутри полых резонаторов с металлическими
стенками или в поперечном сечении волноводов либо в окрестности тонкой проволочной
или щелевой антенны). При этом обычно обращаются к фурье-преобразованию уравнений Максвелла
и представлению поля в виде набора дискретных или квазидискретных мод.
г) 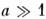 .
В рамках этого неравенства существуют ква-зиоптич. и оптич. приближения (см.
Квазиоптика, Геометрической оптики метод), относящиеся к протяжённым
в масштабе длины волны распространениям полей (волновым пучкам, многомодовым
конфигурациям и т. п.). Под характерным масштабом, входящим в параметр а, здесь
подразумевается масштаб изменения амплитуды поля.
.
В рамках этого неравенства существуют ква-зиоптич. и оптич. приближения (см.
Квазиоптика, Геометрической оптики метод), относящиеся к протяжённым
в масштабе длины волны распространениям полей (волновым пучкам, многомодовым
конфигурациям и т. п.). Под характерным масштабом, входящим в параметр а, здесь
подразумевается масштаб изменения амплитуды поля.
В Международной системе единиц
основная размерная константа - , наз. импеданс (или характеристическое
сопротивление) Эфира 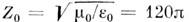 Ом/цикл.
Она в явном виде показывает свойства среды распространения электромагнитных волн
и представляет известные удобства при сопоставлении процессов распространения
плоских волн в свободном пространстве с волнами напряжения и тока в линиях передач,
и показывает, что Эфир имеет две фундаментальные физически размерные характеристики -
электрическую и магнитную проницаемости:
Ом/цикл.
Она в явном виде показывает свойства среды распространения электромагнитных волн
и представляет известные удобства при сопоставлении процессов распространения
плоских волн в свободном пространстве с волнами напряжения и тока в линиях передач,
и показывает, что Эфир имеет две фундаментальные физически размерные характеристики -
электрическую и магнитную проницаемости:
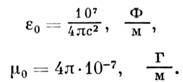
"Таинственный" множитель 2·10-7 возник от произвольного определения силы тока в 1 Ампер, через силовое взаимодействие проводников с током на расстоянии 1 метр.

M. А. Миллер, E, В. Суворов
|
|