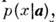 где
где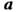 - вектор неизвестных параметров. Определим функцию правдоподобия выражением
- вектор неизвестных параметров. Определим функцию правдоподобия выражениемМаксимального правдоподобия метод - метод оценивания неизвестных параметров для распределения
случайной величины c по наблюдению её реализаций при параметрич.
анализе данных. M. п. м. был предложен P. Э. Фишером (R. A. Fisher) в
1912 и формулируется след, образом. Пусть плотность вероятности величины х есть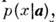 где
где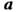 - вектор неизвестных параметров. Определим функцию правдоподобия выражением
- вектор неизвестных параметров. Определим функцию правдоподобия выражением
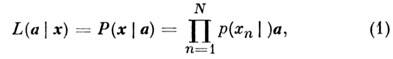
к-рое в отличие от плотности вероятности 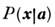 рассматривают как функцию вектора а при
заданном векторе c реализовавшихся значений
рассматривают как функцию вектора а при
заданном векторе c реализовавшихся значений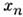 .
Оценкой M. п. м. паз. вектор
.
Оценкой M. п. м. паз. вектор 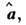 отвечающий максимуму выражения (1) и принадлежащий допустимой области значений
отвечающий максимуму выражения (1) и принадлежащий допустимой области значений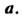 Часто ищут максимум выражения
Часто ищут максимум выражения 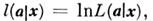 что упрощает задачу поиска
что упрощает задачу поиска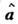 для
экспоненциальных распределений. Идея M. п. м. заключается в том, что данная
реализация вектора
для
экспоненциальных распределений. Идея M. п. м. заключается в том, что данная
реализация вектора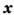 должна отвечать наиболее вероятному значению
должна отвечать наиболее вероятному значению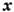 ,
а потому при заданном
,
а потому при заданном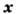 выражение
выражение 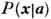 должно принимать макс, значение. Напр., время жизни г нестабильных частиц подчиняется
распределению
должно принимать макс, значение. Напр., время жизни г нестабильных частиц подчиняется
распределению 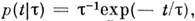 где
где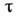 - неизвестный
параметр, характерный для каждой частицы. Пусть измерены времена жизни
- неизвестный
параметр, характерный для каждой частицы. Пусть измерены времена жизни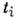 для
N распадов. Если пренебречь ошибками измерений
для
N распадов. Если пренебречь ошибками измерений 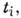 то функция правдоподобия равна
то функция правдоподобия равна
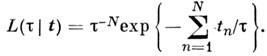
Оценка M. п. м.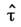 получается
из решения ур-ния правдоподобия
получается
из решения ур-ния правдоподобия
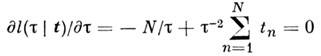
и равна
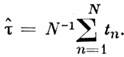
С M. п. м. связано неравенство Крамера - Рао:
дисперсия D (а)оценки параметра а, полученной любым методом,
удовлетворяет неравенству
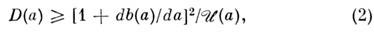
где
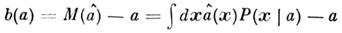
наз. смещением оценки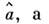
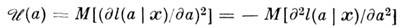
наз. кол-вом информации в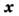 о
параметре а. В случае вектора параметров
о
параметре а. В случае вектора параметров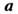 неравенство
(2) обобщается след, образом. Если ввести ср. значения
неравенство
(2) обобщается след, образом. Если ввести ср. значения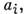
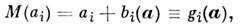
ковариационную матрицу
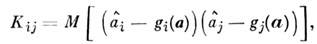
матрицу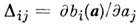 и
информац. матрицу
и
информац. матрицу
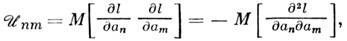
то справедливо неравенство
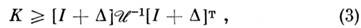
где I -единичная матрица, т означает транспонирование.
Если оценки 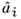 являются
несмещёнными, то для дисперсий
являются
несмещёнными, то для дисперсий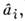 как
это следует из (3), выполняется неравенство
как
это следует из (3), выполняется неравенство
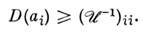
Неравенство Крамера - Рао полезно тем, что позволяет
ещё на стадии планирования эксперимента оценить достижимую точность "измерения"
параметров изучаемых распределений.
При нек-рых ограничениях на 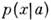 можно показать, что оценка M. п. м. состоятельна,
т. е. при
можно показать, что оценка M. п. м. состоятельна,
т. е. при 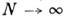 один из корней ур-ния правдоподобия,
один из корней ур-ния правдоподобия, 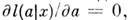 стремится к точному значению а. Оценка M. п. м. асимптотически распределена
по нормальному закону с нулевым ср. значением и дисперсией, равной
стремится к точному значению а. Оценка M. п. м. асимптотически распределена
по нормальному закону с нулевым ср. значением и дисперсией, равной 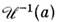 .
.
При конечных N оценка M. п. м., вообще
говоря, является смещённой. Оптим. свойством оценки M. п. м. при конечных N оказывается то, что при нек-рых условиях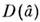 достигает нижней границы, задаваемой неравенством Крамера - Рао (2). В общем
случае свойства оценки M. п. м. можно изучить
при помощи Монте-Карло метода: задавая значение a из области возможных
значений, получают выборку
достигает нижней границы, задаваемой неравенством Крамера - Рао (2). В общем
случае свойства оценки M. п. м. можно изучить
при помощи Монте-Карло метода: задавая значение a из области возможных
значений, получают выборку 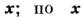 находят оценку
находят оценку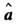 и
строят её среднее значение и ковариационную матрицу. Другое оптимальное свойство
оценки M. п. м.: оценка
и
строят её среднее значение и ковариационную матрицу. Другое оптимальное свойство
оценки M. п. м.: оценка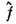 функции
/(а) равна
функции
/(а) равна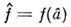 . В
этом её преимущества перед оценкой по наименьших квадратов методу.
. В
этом её преимущества перед оценкой по наименьших квадратов методу.

В. П. Жигунов
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.
|
|