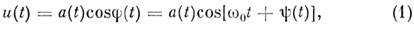
Модулированные колебания. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Модулированные колебания - колебания, параметры к-рых (амплитуда, фаза, частота, длительность и т. п.) изменяются во времени. Это понятие распространяется и на колебания, параметры к-рых изменяются в пространстве, тогда говорят о пространственно модулированных колебаниях; в отличие от временных M. к. они могут быть дву- и трёхмерными. Далее всюду речь идёт только о колебаниях, модулированных во времени. Характер исходных (несущих) колебаний и законы их модуляции разнообразны: от простейших гармонических до хаотических. Это могут быть даже не колебательные, а, напр., импульсные сигналы с переменными длительностью, скважностью или другими характерными для импульсной модуляции параметрами.

Простейшим примером M. к., имеющим принципиальное значение для описания мн. физ. процессов и техн. приложений, является квазигармонич. M. к.:

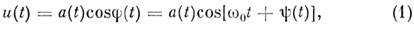
где a(t) - мгновенная амплитуда, j(t) - полная фаза колебаний, w₀ = const - несущая частота, y(t) - фаза колебаний. Все эти величины вводят но аналогии с обычными гармонич. колебаниями, для к-рых a(t) = const и y(t) = const. B произвольном случае представление (1) неоднозначно: множеству пар a(t), f(t) соответствует одна и та же функция u(t), что затрудняет строгий анализ M. к. Обычно эту неоднозначность удаётся устранить и оперировать с амплитудами и фазами как с определ. параметрами M. к. В частности, одним из эвристич. способов устранения неоднозначности является введение дополнит. сигнала u(t), каждая фурье-составляющая к-рого сдвинута по фазе па p/2 относительно соответствующей фурье-составляющей осн. сигнала u(t)(преобразование Гильберта), что приводит к образованию т. н. аналитического сигнала:

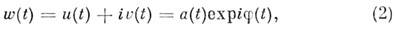
амплитуда a(t)и фаза f(t) к-рого однозначно выражаются через u(t) и u(t):

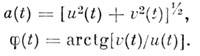
Физически это соответствует мысленной замене осцилляторов ротаторами. Во мн. техн. устройствах, реализующих, напр., приём M. к., преобразование (2) используют как наиболее эфф. "средство" демодуляции.

Интерпретации M. к. как в исходной (1), так и в обобщённой (2) форме совпадают, если предположить медленность изменения функций a(t)и f(t) на протяжении периода T несущей частоты w₀ = 2p/T и пренебречь усреднённым вкладом высших составляющих спектра. Как правило, именно с таким квазигармонич. M. к. приходится иметь дело в технике.

Виды M. к. Итак, в определ. условиях [медленность изменения и (или) возможность доопределения] M. к. можно разделить на амплитудно-модулированные колебания (AMK) и фазомодулированные колебания (ФМК). Последние называют иногда также колебаниями с угл. модуляцией, выделяя среди них частотно-модулированные колебания (ЧМК) и собственно ФМК. Тем не менее, поскольку

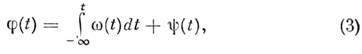
точных критериев различения режимов, в к-рых w(t) = const, ^.y(t)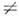

const и y(t) = const, w(t)

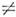const, не существует. Поэтому при проведении такой классификации руководствуются скорее нек-рой "спектральной интуицией", а главное принципами реализации процессов модуляции и демодуляции в соответствующих техн. устройствах.

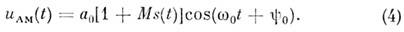
Здесь а₀ - пост. амплитуда несущего колебания (рис., a), s(t) - нормированный [обычно mах|s(t)| =1] модулирующий сигнал (рис., б), M- коэф. модуляции (см. Амплитудная модуляция ).Случай M << 1 соответствует слабомодулированным AMK (рис., в), M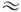

1 - глубокомодулиров. AMK; сигналы с M > 1 наз. перемодулированными (рис., г). При использовании AMK в приёмопередающих системах (вещание, связь и т. п.) выбирают оптимальные (с точки зрения эфф. использования мощности передатчиков и нелинейных искажений формы AMK) значения M. Поскольку передаваемая информация равнозначно заключена в верхних и нижних боковых составляющих спектра AMK, то выгодно формировать и передавать информацию AMK с подавлением одной из групп боковых частот (полос). В этом случае получаются т.н. однополосные M. к., содержащие комбинацию AMK н ФМК, характерные для систем с частотным уплотнением канала передачи и высокой энерготич. эффективностью. Иногда используют частичное или полное подавление несущей компоненты с последующим её восстановлением в приёмной системе.

Квазигармонич. ФМК и ЧМК записывают в виде, аналогичном (4):

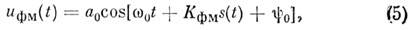
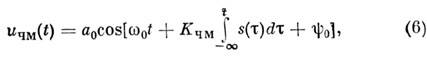
где K_фм, K_чм - коэф., характеризующие девиацию фа-за Df и частоты Dw (рис, д, е). В силу соотношения(3) ф-лы (5) и (6) взаимно связаны, что и позволяет счи-тать ЧМК разновидностью ФМК и наоборот.

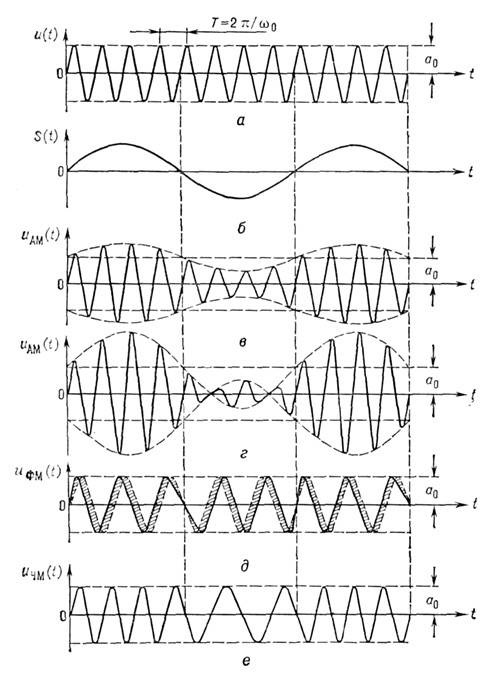
Модулированные колебания: a - несущее (немодулированное) колебание; б - гармоническое модулирующее колебание; в - амплитудно-модулированное колебание; г - перемодулирован-чое колебание; д - фазо-модулированное колебание; е - частотно-модулированное колебание.

Спектры ФМК и ЧМК (см. Частотная модуляция, Фазовая модуляция)существенно сложнее спектра AMK даже в случае гармонич. модуляции и в значит. мере определяются значением индекса модуляции т = Dw/W, характеризующего отношение девиации частоты к частоте W модулирующего сигнала. При т >> 1 (а именно такие значения обычно используют в системах связи) ширина спектра ЧМК равна удвоенной девиации частоты 2Dw = 2mW, тогда как спектр AMK занимает полосу ширины 2W, т. е. в то раз меньшую. Причём для ЧМК девиация частоты пропорц. амплитуде модулирующего сигнала Dw_чм и не зависит от частоты W, а для ФМК, в силу (3), Dw_фм пропорциональна W. Большая "широкополосность" ЧМК и ФМК часто (но не всегда, исключение составляют, напр., случаи оптим. приёма) обусловливает их большую помехоустойчивость по сравнению с AMK.

Др. важными видами M. к., встречающимися в технике и природе, являются колебания, модулированные как по амплитуде, так и по фазе (частоте), а также импульсно-модулиров. колебания - последовательности импульсов с ВЧ-заполнением (см. Импульсная мо-дуляция).

Применения M. к. Фактически все сигналы, используемые в технике и возникающие в естеств. условиях, можно считать M. к. В технике связи, напр., модулирующие сигналы являются информационными, т. е. содержащими передаваемую информацию, тогда как несущее колебание, частота к-рого, как правило много больше ширины спектра информац. сигнала, обеспечивает более эфф. передачу этой информации на расстояние При этом огибающая AMK подвергается случайным изменениям и на трассе распространения и в приёмопередающей аппаратуре (т. е. обладает слабой помехозащищённостью, в особенности в области НЧ), поэтому применение AMK целесообразно там, где важна простота устройств связи и характер сообщения может не пострадать из-за отсутствия или искажения НЧ-компонент спектра. Так, в телевидении для передачи изображения используют однополосные AMK, а для передачи НЧ-спектра звукового сопровождения применяют более помехоустойчивые ЧМК. У ЧМК, однако более широкий спектр по сравнению с AMK, в особенности когда индекс модуляции выбран большим для ослабления действия помех и повышения точности передачи сообщения, что снижает эффективность использования рабочего диапазона частот при ограниченном числе каналов связи.

В радиолокации и радиоастрономии M. к. используют для обнаружения целей и определения их важнейших геом. (размеры, конфигурация) и физ. (температура, плотность, диэлектрич. проницаемость и т. п.) параметров. Для физ. сред характерно появление естеств. модуляции, возникающей при воздействии магн. или электрич полей на излучающие материальные среды (см Зеемана эффект, Штарка эффект); при рассеянии света на колебаниях кристаллич. решётки твёрдых тел (Мандельштама - Бриллюэна рассеяние)и т. д. Понятие естеств. модуляции распространяют также на волны. Так, напр., волновой пучок достаточной интенсивности может изменять параметры среды и, как следствие, модулировать свою плотность (см. Самофо-кисировка света). При распространении волн в нелинейных диспергирующих средах (жидкостях, плазме) возникает явление автомодуляции волн, связанное с разл. видами неустойчивости волн по отношению к НЧ-пространственно-временным возмущениям. Естеств модуляция находит практич. приложение в радио- и оптич. спектроскопии для диагностики параметров разнообразных сред; в нелинейной оптике для формирования мощных световых потоков; в акустике и др областях прикладной физики. Способы практич. реализации M. к. связаны, как правило, с нелинейными устройствами, параметры к-рых (в радиотехнике, напр., это ёмкость, сопротивление; в акустике - плотность, и т. п. ) можно изменять во времени в соответствии с законом модуляции. Техн. устройства, реализующие M. к., наз. модуляторами.

Литература по модулированным колебаниям

Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.