Уравнение Пирогова - дифференциальное ур-ние, описывающее
эволюцию распределения вероятностей для пространственного положения броуновской
частицы. Пусть w(x,t) - плотность вероятности того, что броуновская
частица (см. Броуновское движение)в момент времени t находится
в точке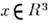 Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию:
Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию: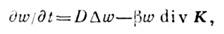 где
где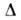 -
Лапласа
оператор, D и
-
Лапласа
оператор, D и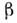 - параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
- параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
Это ур-ние впервые было выведено Пироговым и явилось прообразом
более общих дифференциальных ур-ний в теории марковских диффузионных процессов
(Фоккера
- Планка уравнение, Колмогорова уравнения).
Знаете ли Вы, как разрешается парадокс Ольберса?
(Фотометрический парадокс, парадокс Ольберса - это один из парадоксов космологии, заключающийся в том, что во Вселенной, равномерно заполненной звёздами, яркость неба (в том числе ночного) должна быть примерно равна яркости солнечного диска. Это должно иметь место потому, что по любому направлению неба луч зрения рано или поздно упрется в поверхность звезды.
Иными словами парадос Ольберса заключается в том, что если Вселенная бесконечна, то черного неба мы не увидим, так как излучение дальних звезд будет суммироваться с излучением ближних, и небо должно иметь среднюю температуру фотосфер звезд. При поглощении света межзвездным веществом, оно будет разогреваться до температуры звездных фотосфер и излучать также ярко, как звезды. Однако в дело вступает явление "усталости света", открытое Эдвином Хабблом, который показал, что чем дальше от нас расположена галактика, тем больше становится красным свет ее излучения, то есть фотоны как бы "устают", отдают свою энергию межзвездной среде. На очень больших расстояниях галактики видны только в радиодиапазоне, так как их свет вовсе потерял энергию идя через бескрайние просторы Вселенной. Подробнее читайте в
FAQ по эфирной физике.
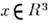 Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию:
Тогда
в предположении, что на эту частицу действует переменное силовое поле K(x,t), плотность w удовлетворяет следующему дифференциальному ур-нию: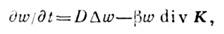 где
где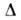 -
Лапласа
оператор, D и
-
Лапласа
оператор, D и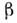 - параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.
- параметры, определяемые массой частицы, вязкостью, температурой среды и т.
д.

