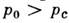
Сопло - канал (труба) переменного по длине поперечного сечения, предназначенный для разгона жидкостей или газов до заданной скорости и придания потоку заданного направления. Служит также устройством для получения газовых и жидкостных струй. Поперечное сечение сопел может быть прямоугольным (плоские сопла), круглым (осесимметричные соплам), иметь форму кольца (кольцевые сопла, сопла с центр. телом) или произвольную форму, в т. ч. форму эллипса или многоугольника (пространственные сопла).
Сопла широко используются в технике: в паровых, водяных и газовых турбинах, в ракетных и воздушно-реактивных двигателях, в газодинамических лазерах, в магнитогидродинамич. установках, в аэродинамических трубах и на газодинамич. стендах, при создании молекулярных пучков, в хим. технологии, в струйных аппаратах, в процессах дутья и др.
В соплах происходит непрерывное увеличение скорости v жидкости или
газа в направлении течения - от начального (обычно малого) значения v0
во входном сечении сопла до наиб. скорости vc на выходе
сопла. При движении по соплу внутр. энергия рабочего тела преобразуется в кинетич.
энергию вытекающей струи, сила реакции к-рой, направленная противоположно
скорости истечения, наз. тягой. В силу закона сохранения энергии одновременно
с ростом скорости в сопле происходит непрерывное падение давления и температуры
от их нач. значений р0, Т0 во входном сечении
сопла до наим. значений рc, Тc в выходном. Т.
о., для реализации течения в сопле необходим нек-рый перепад давления, т.
е. выполнение условия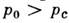
Если считать движение жидкости или газа по соплу изоэнтропийным (см. Изоэнтропийный процесс)и стационарным и рассматривать средние по поперечному сечению S значения давления р, скорости v, плотности р и скорости звука с (одномерное приближение), то из Эйлера ур-ния
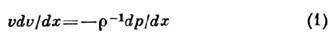
(х - координата вдоль сопла), неразрывности уравнения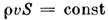 и выражения скорости звука
и выражения скорости звука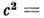
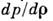 получаем
ур-ние
получаем
ур-ние
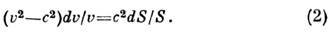
Из него видно, что при v < с (дозвуковое течение по соплу) знак dv противоположен знаку dS, т. е. для того, чтобы скорость течения по соплу росла (dv > 0), площадь сечения с ростом х должна уменьшаться (dS < 0), а при v > с (сверхзвуковое течение по соплу) знаки dv и dS одинаковы, т. е. для получения роста скорости (dv > 0) необходимо увеличивать и плошадь S вдоль сопла (dS > 0). Физически это связано с тем, что при сверхзвуковой скорости течения газов из-за влияния сжимаемости плотность газа падает быстрее, чем растёт скорость вдоль сопла, и в силу ур-ния неразрывности для компенсации быстрого падения плотности необходимо увеличивать площадь S. Если v = с, то dS = 0 и функция S(x)принимает экстремальное (минимальное) значение. Т. о., дозвуковое сопло имеет сужающуюся форму (рис. 1).
наиб. скорость, к-рую можно получить в сужающемся сопле, равна скорости
звука и достигается в его выходном (наиб. узком) сечении. Сверхзвуковое
сопло, называемое также соплом Лаваля по имени его изобретателя - швед. инженера
К. Г. П. де Лаваля (К. G. P. de Laval), имеет вначале сужающуюся, а затем
расширяющуюся форму (рис. 2). Давление рс в выходном
сечении дозвукового сопла всегда равно давлению ра в окружающей
среде, куда происходит истечение из сопла (pc = pа). При возрастании р0 и неизменном ра скорость vc в
выходном сечении дозвукового сопла сначала
увеличивается, а после того как р0 достигнет нек-рой
определ. величины, vc становится постоянной и при дальнейшем
увеличении р0 не изменяется. Такое явление наз. кризисом
течения в сопле. После наступления кризиса ср. скорость истечения из дозвукового
сопла равна местной скорости звука (v = с)и наз. критической скоростью.
В этом случае все параметры газа в выходном сечении сопла также наз. критическими,
а сопло называется звуковым.
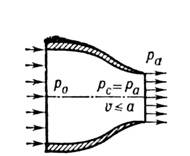
Рис. 1. Схема дозвукового сопла.
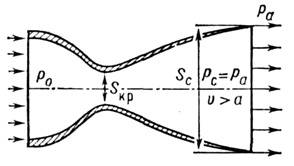
Рис. 2. Схема сверхзвукового сопла.
В сверхзвуковом сопле критическим наз. его наиб. узкое сечение. Кривая
линия, на к-рой реализуется переход от дозвуковой к сверхзвуковой скорости
течения (линия v = с), расположена в области мин. сечения сопла, поэтому
ср. скорость в критич. сечении всегда близка к скорости звука. относит.
скорость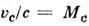 и
давление
и
давление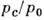 в выходном сечении сверхзвукового C. зависят только от отношения площади
выходного сечения Sc к площади критич. сечения и не зависят
в широких пределах от изменения относит. давления p0/pа.
Давление в выходном сечении сверхзвукового сопла может быть равно давлению
в окружающей среде (pc = pа)'
такой режим течения в сопле наз. расчётным, в противном случае - нерасчётным.
Нерасчётные режимы характеризуются образованием волн разрежения вне сопла
в случае рс > ра или ударных волн вне или внутри сопла в случае рс < ра. Когда поток проходит через систему волн разрежения или ударных волн,
давление становится равным ра.
в выходном сечении сверхзвукового C. зависят только от отношения площади
выходного сечения Sc к площади критич. сечения и не зависят
в широких пределах от изменения относит. давления p0/pа.
Давление в выходном сечении сверхзвукового сопла может быть равно давлению
в окружающей среде (pc = pа)'
такой режим течения в сопле наз. расчётным, в противном случае - нерасчётным.
Нерасчётные режимы характеризуются образованием волн разрежения вне сопла
в случае рс > ра или ударных волн вне или внутри сопла в случае рс < ра. Когда поток проходит через систему волн разрежения или ударных волн,
давление становится равным ра.
В более общем случае неизоэнтропийного и неадиабатич. течения в сопле ур-ние типа (2) включает члены, учитывающие трение, подвод или отвод теплоты, массы и механич. работы к рабочему телу. С учётом этих воздействий переход скорости течения через скорость звука может происходить не только в геометрическом - сначала сужающемся, а затем расширяющемся сопле, но и при изменении знака воздействия на поток в канале пост. сечения. Так, дозвуковой поток в таком канале ускоряется при подводе теплоты (тепловое С.), массы (расходное С.), совершении газом механич. работы (механическое С.), а сверхзвуковой - при изменении знака этих воздействий на обратный. Под влиянием одностороннего воздействия величину скорости газового потока можно довести только до критической (до скорости звука), но нельзя перевести через неё.
Изменение скорости вдоль геом. С. определяется законом изменения площади S(x)по длине С. Контур С., т.е. вид функции S(x)в одномерном приближении, определить нельзя. Поэтому развита теория двумерных (плоских и осесимметричных) и трёхмерных (пространственных) течений в С., основанная на решении (гл. обр. численными методами с использованием ЭВМ) осн. дифференц. ур-ний газовой динамики с соответствующими граничными и нач. условиями. В теории С. решаются две задачи: прямая - определение течения в С., контур к-рого задан, обратная - определение контура С., обладающего к--л. заданными свойствами. Напр., в аэродинамич. трубе С. должно обеспечить создание на выходе, т. е. в рабочей части аэродинамич. трубы, однородного (по величине и направлению) потока с заданной скоростью (или Маха числом Мс = vc/c), а контур С. ракетных и воздушно-реактивных двигателей определяют так, чтобы получить макс. импульс потока на выходе С. (макс. тягу) при заданных ограничениях массы и габаритов С. Чтобы удовлетворить поставленным требованиям в широком диапазоне изменения условий течения (напр., изменения числа Маха С. аэродинамич. труб, скорости и высоты полёта летат. аппарата с ракетным или воздушно-реактивным двигателем), применяют регулируемые С. В сверхзвуковых С. аэродинамич. труб и дозвуковых С. двигателей применяют механич. регулирование площади критич. сечения С. Sкp, что позволяет путём изменения отношения Sкр/Sс изменять число Маха и давление на выходе С., а в сверхзвуковых С. двигателей с той же целью кроме регулирования Sкр используют выдвижные (телескопические), раскрываемые и разворачивающиеся насадки, дискретным образом изменяющие Sc.
Теория С. рассматривает течение реального рабочего тела в С.и учитывает трение, теплообмен рабочего тела со стенками С., наличие в газовом потоке жидких и твёрдых частиц (см. Двухфазное течение ),неравновесных хим. реакций и физ. процессов возбуждения внутр. степеней свободы молекул, переноса лучистой энергии, воздействия эл--магн. полей и др. Все эти процессы, связанные с отличием рабочего тела от идеального газа, приводят к возникновению разл. вида потерь в С., уменьшающих тягу двигателей или кпд турбин. Развитие теории С. дало ответ на многие принципиальные вопросы изучения движения жидкостей и газов. Наряду с теорией С. разработаны сложные эксперим. методы исследования течения в С., потребовавшие создания спец. гидродинамич. установок и газодинамич. стендов, а также системы измерения сил и параметров течения.

С. Л. Вишневецкий
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|