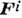 ,
возникающие вследствие взаимодействия между телами или частями данной системы,
и внешние
,
возникающие вследствие взаимодействия между телами или частями данной системы,
и внешние 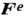 , являющиеся
результатом взаимодействия тел системы с телами, не входящими в данную систему.
, являющиеся
результатом взаимодействия тел системы с телами, не входящими в данную систему.Динамика (от греч. dynamis - сила) - раздел механики, посвящённый изучению движения материальных
тел под действием приложенных к ним сил. Движения любых материальных тел (кроме
микрочастиц), происходящие со скоростями, не близкими к скорости света, изучаются
в т. н. классич. Д. Движение тел, перемещающихся со скоростями, приближающимися
к скорости света, рассматривается в теории относительности (см. Относительности
теория), а движение микрочастиц - в квантовой механике. Эта статья
касается только вопросов классич. Д.
Обычно классич. Д. разделяют
на Д. материальной точки и Д. системы материальных точек. Самостоят. разделами
Д. системы материальных точек (частиц) являются: Д. абсолютно твёрдого тела,
Д. упруго или пластически деформируемого твёрдого тела (см. Упругости теория и Пластичности теория ),Д. жидкости и газа (см. Гидродинамика,
Аэродинамика и Газовая динамика)и др.
Движение любой материальной
системы зависит от её инертности и от действующих на систему сил. Инертность
материальной точки характеризуется массой т этой точки. Инертность материального
тела при поступат. движении определяется величиной M его суммарной массы,
равной сумме масс частиц, образующих тело. При вращат. движении инертность зависит
от распределения масс в занимаемом телом объёме и характеризуется величиной,
наз. моментом инерции тела относительно оси вращения. При сложном движении
инертность тела характеризуется его суммарной массой, положением центра масс
или центра инерции тела и моментами инерции относительно гл. осей инерции, проходящих
через центр масс, или тензором инерции.
Действующие на систему
силы могут быть постоянными или переменными. Перем. силы изменяются определ.
образом в зависимости от времени движения, от положения тела в пространстве
и от его скорости (см. Сила). При этом по отношению к данной механич.
системе действующие силы разделяют на внутренние 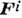 ,
возникающие вследствие взаимодействия между телами или частями данной системы,
и внешние
,
возникающие вследствие взаимодействия между телами или частями данной системы,
и внешние 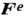 , являющиеся
результатом взаимодействия тел системы с телами, не входящими в данную систему.
, являющиеся
результатом взаимодействия тел системы с телами, не входящими в данную систему.
Классич. Д. базируется
на трёх осн. законах, наз. законами Ньютона, к-рые можно формулировать след.
образом (формулировку, данную Ньютоном, и соответствующие пояснения см. в ст.
Ньютона законы механики). 1) Если на материальную точку не действуют
никакие силы (или если приложенные к ней силы взаимно уравновешиваются), то
по отношению к инерциалъной системе отсчёта материальная точка будет
находиться в состоянии покоя или равномерного прямолинейного движения.
2) Если на материальную
точку действует сила F, то точка получает по отношению
к инерциальной системе отсчёта такое ускорение 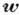 ,
что произведение массы т точки на это ускорение равно силе:
,
что произведение массы т точки на это ускорение равно силе:

3) Две материальные точки
действуют друг на друга с силами, равными по абс. величине и направленными в
противоположные стороны вдоль прямой, соединяющей эти точки.
К осн. законам Д. присоединяют
ещё закон независимости действия сил, согласно к-рому при одноврем. действии
на материальную точку неск. сил каждая из сил сообщает точке такое же ускорение,
какое она сообщила бы, действуя одна.
Из названных законов как
следствия получаются все ур-ния и теоремы Д. В Д. рассматриваются решения двух
типов задач: 1) зная закон движения данного тела (т. е. ур-ния, определяющие
положение тела в пространстве в любой момент времени), найти силы, под действием
к-рых это движение происходит; 2) зная силы, действующие на данное тело или
систему тел, определить закон движения этого тела или системы. Второй тип задач
является в Д. основным.
Задачи Д. решаются с помощью
дифференц. ур-ний движения, к-рыми устанавливается зависимость между действующими
на систему силами, величинами, характеризующими инертность движущейся системы,
и параметрами, определяющими её положение в пространстве (или скорости её части).
Для одной материальной
точки это ур-ние даётся 2-м законом Д. и выражается векторным равенством (1).
В проекциях на оси прямоугольной декартовой системы координат получаются след.
3 дифференц. ур-ния движения материальной точки:
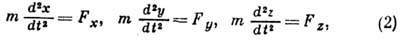
где t - время, х,
у, z - координаты движущейся точки. При действии на точку неск. сил 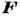 обозначает их равнодействующую. По ур-ниям (2) можно, зная закон движения точки,
т. е. х, у, z как функции времени t, определить действующую силу
(1-я задача Д.) или, зная проекции действующих сил как функции времени, координат
и скорости точки, найти закон её движения, т. е. x(t), y(t),
z(t) (2-я, или основная, задача Д.).
обозначает их равнодействующую. По ур-ниям (2) можно, зная закон движения точки,
т. е. х, у, z как функции времени t, определить действующую силу
(1-я задача Д.) или, зная проекции действующих сил как функции времени, координат
и скорости точки, найти закон её движения, т. е. x(t), y(t),
z(t) (2-я, или основная, задача Д.).
Для любой материальной
системы дифференц. ур-ния движения находятся как следствие из 2-го и 3-го законов
Д. В частности, для абсолютно твёрдого тела в зависимости от вида его движения
получаются таким путём след. результаты. Если тело движется поступательно, то
дифференц. ур-ния его движения имеют вид ур-ний (2), где только т - масса
всего тела, х, у, z - координаты его центра масс. Если тело вращается
вокруг неподвижной оси, то дифференц. ур-ние его движения имеет вид:

где 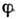 - угол поворота тела, Iz - момент инерции тела относительно
оси вращения z, Мz - гл. момент действующих сил относительно
той же оси. Движение твёрдого тела вокруг неподвижной точки описывается тремя
динамич. ур-ниями Эйлера (см. Эйлера уравнение ).Наконец, движение свободного
твёрдого тела описывается в общем случае шестью дифференц. ур-ниями; первые
3 совпадают с ур-ниями поступательного движения, а остальные являются динамич.
ур-ниями Эйлера, в к-рых лишь осями, связанными с телом, следует считать его
гл. центральные оси инерции.
- угол поворота тела, Iz - момент инерции тела относительно
оси вращения z, Мz - гл. момент действующих сил относительно
той же оси. Движение твёрдого тела вокруг неподвижной точки описывается тремя
динамич. ур-ниями Эйлера (см. Эйлера уравнение ).Наконец, движение свободного
твёрдого тела описывается в общем случае шестью дифференц. ур-ниями; первые
3 совпадают с ур-ниями поступательного движения, а остальные являются динамич.
ур-ниями Эйлера, в к-рых лишь осями, связанными с телом, следует считать его
гл. центральные оси инерции.
Для деформируемых твёрдых
тел, жидкостей и газов дифференц. ур-ния движения являются ур-ниями в частных
производных. При решении задач Д. к ним должны присоединяться ур-ние, выражающее
закон постоянства масс, и ур-ния, характеризующие нек-рые физ. свойства среды
(напр., зависимость для данной среды плотности от давления или напряжений от
деформаций и т. п.).
Дифференц. ур-ния движения
материальной системы могут быть получены не только из осн. законов, но и из
др. общих принципов Д., в частности из вариационных принципов механики или
из Д-Аламбера принципа .Один из основных принципов механики - Д-Аламбера
- Лагранжа принцип - приводит к т. н. общему ур-нию Д.:
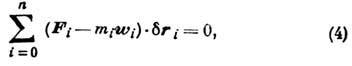
где 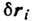 - векторы возможных перемещений точек системы.
- векторы возможных перемещений точек системы.
Чтобы с помощью дифференц.
ур-ний движения найти закон движения системы, надо кроме действующих сил знать
ещё т. н. нач. условия, т. е. положения и скорости точек системы в к--н. момент
времени, принимаемый за начальный. По нач. условиям определяются значения
постоянных интегрирования, к-рые входят в общие решения дифференц. ур-ний движения.
Для деформируемых, жидких и газообразных тел должны ещё задаваться т. н. граничные
условия.
Для систем тел, движения
к-рых ограничены связями механическими (нитями, стержнями и т. п.), дифференц.
ур-ния движения составляются с помощью принципа освобождаемости, согласно к-рому
несвободную систему можно рассматривать как свободную, отбросив связи и заменив
их действие соответствующими силами, наз. реакциями связей. При этом
осн. задача Д. распадается на две, а именно: зная действующие на систему заданные
силы, определить закон движения системы и реакции наложенных связей.
В наиболее часто встречающемся
случае т. н. голономных связей, т. е. связей, налагающих ограничения только
на положения точек системы, но не на их скорости (ур-ния этих связей не содержат
производных от координат), дифференц. ур-ния, служащие для определения закона
движения системы, могут быть составлены в форме, предложенной Лагранжем (см.
Лагранжа уравнения механики). Преимущество этих ур-ний состоит в том,
что число их не зависит от числа точек или тел, входящих в систему, и равно
числу степеней свободы системы (см. Степеней свободы число ),а также
в том, что эти ур-ния не содержат в себе наперёд неизвестных реакций связей.
Реакции связей, когда закон движения системы известен, могут определяться с
помощью принципа Д-Аламбера.
При изучении относит. движения
тел, т. е. движения относительно систем, как-то перемещающихся по отношению
к инерциальной системе отсчёта, дифференц. ур-ния движения могут составляться
так же, как и для инерциальных ("неподвижных") систем, если к непосредственно
действующим на тело силам взаимодействия с др. телами прибавить т. н. переносные
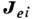 и Kориолиса
и Kориолиса 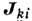 силы
инерции. При этом для каждой материальной точки
силы
инерции. При этом для каждой материальной точки 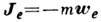 ,
, 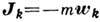 , где т -
масса точки,
, где т -
масса точки, 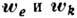 -
её переносное и Кориолиса ускорения (см. Кинематика ).Напр., для одной
материальной точки ур-ние относит. движения имеет вид
-
её переносное и Кориолиса ускорения (см. Кинематика ).Напр., для одной
материальной точки ур-ние относит. движения имеет вид
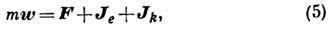
где 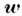 - относит. ускорение точки.
- относит. ускорение точки.
Относит. движение может
изучаться также с помощью ур-ний Лагранжа, если ввести в них параметры, определяющие
положение тела по отношению к подвижным осям.
Все обычно применяемые
в Д. дифференц. ур-ния движений, напр. (2), (3) или ур-ния Лагранжа, являются
ур-ниями 2-го порядка и содержат в качестве неизвестных координаты (параметры),
определяющие положение системы. Но в нек-рых случаях для решения задач Д. (а
также в статистич. физике, квантовой механике и др.) пользуются т. н. канонич.
ур-ниями механики, или Гамильтона уравнениями ,к-рые представляют собой
систему дифференц. ур-ний 1-го порядка и содержат в качестве неизвестных не
только координаты, но и импульсы (обобщённые).
Кроме дифференц. ур-ний
движения для решения задач Д. широко используются вытекающие из этих ур-ний
т. н. общие теоремы Д. Значение общих теорем состоит в том, что они устанавливают
важные физ. зависимости между основными динамич. характеристиками движения и
взаимодействия материальных тел, открывая тем самым новые возможности исследования
механич. движений и часто упрощая процесс решения соответствующих задач. Кроме
того, общие теоремы позволяют изучать отд. практически важные стороны данного
явления, не изучая явления в целом.
К общим теоремам Д. относятся
следующие. 1) Теорема об изменении кол-ва движения 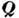 системы:
изменение кол-ва движения системы за любой промежуток времени равняется геом.
сумме импульсов
системы:
изменение кол-ва движения системы за любой промежуток времени равняется геом.
сумме импульсов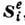 ,
действующих на систему
внеш. сил (см. Импульс силы)за тот же промежуток времени:
,
действующих на систему
внеш. сил (см. Импульс силы)за тот же промежуток времени:
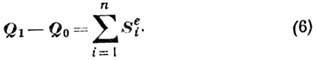
Из теоремы вытекает закон
сохранения количества движения: если геом. сумма всех действующих на систему
внеш. сил равна нулю, то количество движения системы остаётся всё время величиной
постоянной. Теорема применяется при изучении движения жидкостей, в теории удара,
в теории реактивного движения и др. Следствием этой теоремы является также теорема
о движении центра масс: центр масс механич. системы движется как материальная
точка, масса к-рой равна массе системы и на к-рую действуют все внеш. силы,
приложенные к системе.
2) Теорема об изменении
гл. момента количеств движения (кинетич. момента) системы 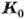 :
производная по времени от гл. момента количеств движения системы относительно
любого неподвижного центра (или оси) равна сумме моментов действующих внеш.
сил относительно того же центра (или оси):
:
производная по времени от гл. момента количеств движения системы относительно
любого неподвижного центра (или оси) равна сумме моментов действующих внеш.
сил относительно того же центра (или оси):
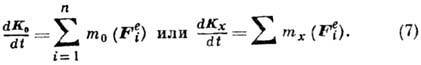
Эта теорема справедлива
также для движения системы относительно осей, перемещающихся поступательно вместе
с центром масс. Из теоремы вытекает закон сохранения гл. момента количеств движения:
если сумма моментов внеш. сил относительно данного центра (или оси) равна нулю,
то гл. момент количеств движения системы относительно этого центра (или оси)
остаётся всё время величиной постоянной. Теорема применяется при изучении движения
твёрдого тела, в частности в теории гироскопов ,в теории удара, при изучении
движения планет, в теории турбин.
3) Теорема об изменении
кинетич. энергии T системы: изменение кинетич. энергии системы при любом
её перемещении равняется сумме работ Аi всех приложенных сил
на том же перемещении:
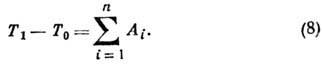
В случае, когда все действующие
силы потенциальны (см. Потенциальные силы), из теоремы вытекает
закон сохранения механич. энергии: при движении под действием потенц. сил сумма
кинетич. и потенц. энергий системы остаётся величиной постоянной. Теорема широко
применяется для решения разнообразных задач Д.
Помимо установления общих
методов изучения движения тел под действием сил в Д. рассматривается также ряд
спец. задач: теория гироскопа, теория механич. колебаний, теория устойчивости,
движения, теория удара, механика тел переменной массы и др.
В результате применения методов Д. к изучению движения отд. конкретных объектов
возник ряд спец. дисциплин: небесная механика, внешняя баллистика, Д. самолёта,
Д. ракет и т. п.

С. M. Торг
|
|