Знаете ли Вы, в чем фокус эксперимента Майкельсона?
Эксперимент А. Майкельсона, Майкельсона - Морли - действительно является цирковым фокусом, загипнотизировавшим физиков на 120 лет.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
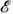), где N(
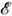)- плотность одночастичных состояний с определ. проекцией спина. Тепловое возбуждение
испытывают лишь квазичастицы в интервале энергий ~kT вблизи уровня Ферми
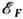; при kT<<
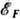их число ~2N(
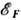)kT, а их тепловая энергия ~2N(
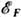)(kT)2, следовательно, Cэ~2N(
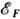)k2T. Т. о., теплоёмкость вырожденного газа электронов или дырок подчиняется линейному
закону и при достаточно низких Т может превзойти решёточную теплоёмкость
Ср=bТ3. Более детальный расчёт при тех же условиях
приводит к ф-ле: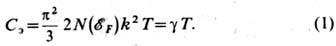
).
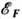Для разделения электронного и решёточного вкладов в теплоёмкость данные о полной
низкотемпературной теплоёмкости обычно аппроксимируют полиномом нечётных степеней
по T:
)
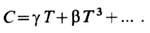
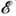имеет выраженную структуру. Напр., если тепловое движение электрона представляет
собой переходы между двумя уровнями, разделёнными энергетич. щелью Д, то Э.
т. имеет т. н. аномалию Шоттки: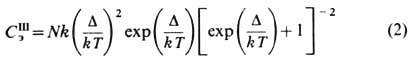
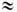1,43gТс. Этот факт используют для идентификации перехода проводника в состояние объёмной
