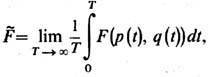
Эргодическая гипотеза в статистической физике - предположение, что
средние по времени значения физ. величин, характеризующих систему, равны
их средним статистическим. Предложена Л. Больцманом в 1887 для обоснования
статистической физики.
В классич. статистич. физике равновесных систем Э. г. основана на предположении, что средние по времени от
фазовых переменных (функций, зависящих от координат q и импульсов р всех частиц замкнутой и энергетически изолированной системы), взятые вдоль
траектории движения системы в фазовом пространстве, равны средним статистическим
по равномерному распределению фазовых точек в тонком (в пределе - бесконечно
тонком) слое вблизи поверхности постоянной энергии. В квантовой статистич. физике
Э. г. есть предположение, что все энергетич. состояния в тонком слое вблизи
поверхности постоянной энергии равновероятны. Э. г. эквивалентна, т. о., предположению,
что замкнутая система (как классическая, так и квантовая) может быть описана
микроканоническим распределением Гиббса. Напр., для классических замкнутых
систем из N частиц с Гамильтона функцией HN (p, q)в
объёме V почти всегда существуют средние по времени от функции фазовых
переменных F(p(t), q(t))
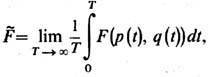
где эволюция р (t),
q (t)во времени определяется из решения ур-ний Гамильтона. Согласно Э.
г.,
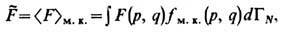
где dГN=dpdq/N!h3N - элемент фазового объёма в безразмерных переменных; fм.к.(р,
q)-микроканонич. распределение, имеющее вид
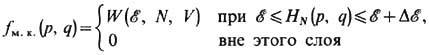
(интегрирование проводится
по всем "микроскопическим" состояниям системы, энергия к-рых лежит
в слое энергии шириной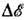 
);
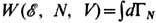-статистический
вес, связанный с энтропией S соотношением S=k ln W.
Делались попытки обоснования эргодической гипотезы с помощью исследования свойств фазовых траекторий замкнутых изолированных механич. систем из большого числа частиц. Были доказаны эргодические теоремы (см. Эргодическая теория ),к-рые сводили Э. г. к предположению о специфич. свойстве фазового пространства (его метрической неразложимости). Однако для обоснования статистич. физики эти теоремы не являются необходимыми, т. к. фазовые траектории чрезвычайно чувствительны к малым возмущениям (см. Размешивание). В частности, они очень чувствительны к малейшему нарушению изоляции или замкнутости системы. Аналогичным свойством чувствительности квантовых состояний к малым возмущениям обладают и квантовые системы.
Д. Н. Зубарев
|
|
 |
