Андерсоновская локализация - явление, возникающее при распространении волн в среде с пространственными неоднородностями
и состоящее в том, что вследствие многократного рассеяния на неоднородностях
и интерференции рассеянных волн становится невозможным распространение бегущих
волн; колебания приобретают характер стоячей волны, сконцентрированной (локализованной)
в ограниченной области пространства. А. л. возможна для волн любой природы,
но особенно ярко она проявляется в случае волн де Бройля для частиц и квазичастиц при изучении кинетич. свойств (электропроводности, теплопроводности) неупорядоченных
твёрдых сред (аморфные вещества, сильно легированные полупроводники и др.),
т. к. при А. л. подвижность частиц равна 0. Представление о возможности локализации
частиц и квазичастиц в неупорядоченных системах было впервые выдвинуто в 1958
Ф. У. Андерсоном (Ph. W. Anderson). С его именем и именем Н. Ф. Мотта (N. F.
Mott) связаны как введение этих понятий в физику аморфных проводников, так и
дальнейшее развитие теории (см. Аморфные и стеклообразные полупроводники,
Аморфные металлы, Неупорядоченные системы).
Спектр энергий частиц в такой среде,
напр. электрона в аморфном твёрдом теле, можно разделить на 2 области значений
энергии e,
для к-рых подвижность mK0
(подвижные или проводящие состояния) и m=0
(локализованные или непроводящие состояния).

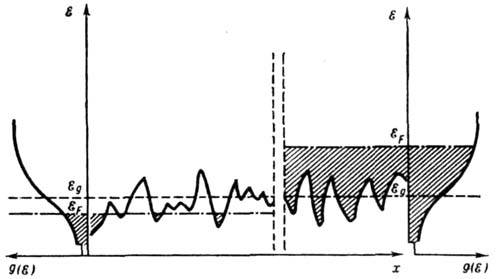
Схематическое изображение энергии электрона
в поле потенциала в случае хаотически расположенных неоднородностей. Пунктир
показывает положение порога подвижности 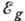 по краям плотности состояний
по краям плотности состояний 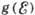 и их заполнения, соответствующие андерсоновскому диэлектрику (слева) и металлу
(справа). Штрих-пунктирная линия показывает положение энергии Ферми
и их заполнения, соответствующие андерсоновскому диэлектрику (слева) и металлу
(справа). Штрих-пунктирная линия показывает положение энергии Ферми 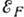 .
Заштрихованы заполненные энергетич состояния в области подвижных состояний электрона.
.
Заштрихованы заполненные энергетич состояния в области подвижных состояний электрона.
Граница eg
между этими областями наз. порогом подвижности (рис.). Пусть волновой пакет
в нач. момент находится в начале координат. Если его энергия соответствует области
подвижных состояний частицы, то за большое время t пакет сильно расплывается,
так что ср. квадрат радиуса R распределения плотности вероятности обнаружить
частицу равен
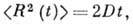 (1)
(1)
где D - коэф. диффузии, связанный
с подвижностью частиц соотношением Эйнштейна. Если же энергия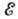 соответствует области локализов. состояний, то рас-плывание волнового пакета
ограничено и при достаточно больших временах
соответствует области локализов. состояний, то рас-плывание волнового пакета
ограничено и при достаточно больших временах  примет вид предельного распределения плотности вероятности:
примет вид предельного распределения плотности вероятности:
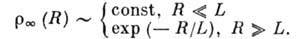 (2)
(2)
Характерный размер этого распределения L наз. длиной локализации. В случае одномерного (случайного) потенциала все состояния частицы локализованы, каким бы слабым ни был случайный потенциал. При этом для состояния с большой энергией длина локализации L равна по порядку величины длине l свободного пробега частицы (в приближении однократного рассеяния).
В двумерном случае все состояния также
локализованы, но длина локализации экспоненциально возрастает при возрастании
энергии. В трёхмерном случае справедлив т. н. критерий локализации Иоффе - Регеля
- Мотта: если длина волны де Бройля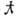 частицы, в частности электрона, меньше, чем длина свободного пробега l, то
состояния являются подвижными; при
частицы, в частности электрона, меньше, чем длина свободного пробега l, то
состояния являются подвижными; при 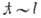 имеется порог подвижности
имеется порог подвижности 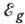 и все состояния с энергией
и все состояния с энергией 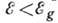 локализованы.
локализованы.
Реальные плёнки и проволоки ведут себя
как двумерные и одномерные проводники, но длина локализации в них больше (из-за
наличия поперечного движения). Так, в проволоке длина локализации L совпадает
с длиной проволоки такого же сечения, сопротивление к-рой 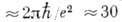 кОм (е - заряд электрона). Для реальных проводников существует критерий
Туалеса: если сопротивление образца при Т=0К больше, чем 30 кОм, то его
размер превышает длину локализации.
кОм (е - заряд электрона). Для реальных проводников существует критерий
Туалеса: если сопротивление образца при Т=0К больше, чем 30 кОм, то его
размер превышает длину локализации.
Если состояния в случайном потенциале,
обусловленном примесями, заполнены электронами так, что уровень Ферми лежит
в области локализов. состояний, то статич. электропроводимость вещества при
Т=0К равна 0 (андерсоновский диэлектрик). Отличие этого состояния от
состояния обычных кристаллич. диэлектриков состоит в том, что плотность состояния
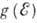 на уровне Ферми
на уровне Ферми 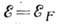 отлична от 0. Поэтому проводимость
отлична от 0. Поэтому проводимость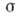 при низкой частоте
при низкой частоте 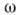 приложенного электрич. поля не пропорциональна
приложенного электрич. поля не пропорциональна 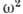 (см. Диэлектрические потери ),а удовлетворяют ф-ле Мотта-Березинского:
(см. Диэлектрические потери ),а удовлетворяют ф-ле Мотта-Березинского:
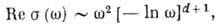 (3)
(3)
где d - размерность пространства.
При 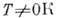 проявляется прыжковая проводимость: электрон проводит длит. время в локализов.
состоянии с энергией
проявляется прыжковая проводимость: электрон проводит длит. время в локализов.
состоянии с энергией 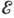 ,
изредка перепрыгивая благодаря взаимодействию с фо-нонами в др. локализов. состояние
с энергией
,
изредка перепрыгивая благодаря взаимодействию с фо-нонами в др. локализов. состояние
с энергией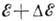 Состояния
с разл. энергией локализованы вблизи разл. точек пространства, поэтому прыжки
с передачей энергии приводят к пространственному перемещению электронов. При
низких темп-pax прыжковая проводимость описывается законом Мотта:
Состояния
с разл. энергией локализованы вблизи разл. точек пространства, поэтому прыжки
с передачей энергии приводят к пространственному перемещению электронов. При
низких темп-pax прыжковая проводимость описывается законом Мотта:
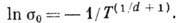 (4)
(4)
При этом характерная передача энергии
при прыжке 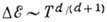 , а длина
прыжка
, а длина
прыжка 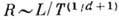 . При возрастании
Т значение R сравнивается с расстояниями между центрами локализации
(в легиров. полупроводниках со ср. расстоянием между примесями). При этом моттовский
режим прыжков переменной длины сменяется режимом прыжков на соседнюю примесь,
а закон Мотта (4) переходит в выражение:
. При возрастании
Т значение R сравнивается с расстояниями между центрами локализации
(в легиров. полупроводниках со ср. расстоянием между примесями). При этом моттовский
режим прыжков переменной длины сменяется режимом прыжков на соседнюю примесь,
а закон Мотта (4) переходит в выражение:
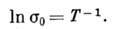
Фазовый переход в неупорядоченной среде, при к-ром уровень Ферми проходит через порог подвижности, наз. переходом Андерсона. В точке перехода L обращается в бесконечность, а при сколь угодно малом смещении уровня Ферми в сторону подвижных состояний появляется отличная от 0 статич. проводимость. Дискуссия о том, появляется ли проводимость скачком (фазовый переход первого рода) или возрастает непрерывно (фазовый переход второго рода), пока не закончилась, но вторая точка зрения является более аргументированной.
При описании поведения электронов в
реальных неупорядоченных системах (аморфных твёрдых телах или кристаллич. полупроводниках
с большой концентрацией примесей)
необходимо учитывать кулоновское взаимодействие между электронами. Оно приводит
к образованию т. н. кулоновской щели - провала плотности состояний 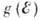 при
при 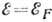 , к видоизменению
закона Мотта и др.
, к видоизменению
закона Мотта и др.

Д. Е. Хмельницкий
|
|