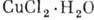 при гелиевых темп-pax в полях неск. кЭ на частоте 9,4 ГГц.
при гелиевых темп-pax в полях неск. кЭ на частоте 9,4 ГГц. АНТИФЕРРОМАГНИТНЫЙ РЕЗОНАНС - электронный
магнитный резонанс в антиферромагнетиках - явление относительно
большого избират. отклика магн. системы антиферромагнетика на периодич. воздействие
эл--магн. поля с частотой, близкой к собств. частотам системы. Это явление сопровождается
сильным поглощением энергии электромагнитного поля антиферромагнетиком (АФ).
А. р. был открыт в 1951 нидерл. физиками
[К. Гортер (С. J. Gorter) и др.] в орторомбич. АФ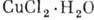 при гелиевых темп-pax в полях неск. кЭ на частоте 9,4 ГГц.
при гелиевых темп-pax в полях неск. кЭ на частоте 9,4 ГГц.
С квантовой точки зрения А. р. можно
рассматривать как резонансное превращение фотонов эл--магн. поля в магноны с
волновым вектором к=0. Квантовое решение задачи об А. р. сводится к определению
спектра магнонов с к=0.
С классич. точки зрения при А. р. резко
возрастает амплитуда вынужденных связанных колебаний векторов намагниченности
подрешёток магнитных под действием магн. компонента эл--магн. поля. Вид
и частота связанных колебаний существенно зависят от магнитной атомной структуры АФ, к-рая может меняться с температурой и величиной внеш. магн. поля. Собств.
частоты колебаний, как правило, зависят от внеш. магн. поля. Эти зависимости
наз. спектром А. р. Вид и частоты намагниченностей подрешёток в АФ находят из
уравнений, написанных для намагниченностей Mj всех подрешёток:
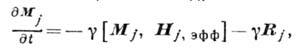
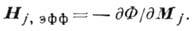 (1)
(1)
Здесь 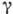 - магнитомеханическое отношение ,
- магнитомеханическое отношение ,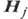 ,
эфф - эфф. магн. поле,
,
эфф - эфф. магн. поле, 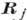 - слагаемые, определяющие диссипацию энергии, Ф - свободная энергия,
записанная как функция
- слагаемые, определяющие диссипацию энергии, Ф - свободная энергия,
записанная как функция 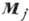 с учётом магн. симметрии АФ. Решения ур-ний (1) могут быть записаны в виде
с учётом магн. симметрии АФ. Решения ур-ний (1) могут быть записаны в виде
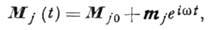 (2)
(2) где 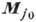 - намагниченности подрешёток в осн. состоянии, тj
-комплексная амплитуда их колебаний. Подставляя (2) в (1) и считая, что
- намагниченности подрешёток в осн. состоянии, тj
-комплексная амплитуда их колебаний. Подставляя (2) в (1) и считая, что
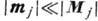 , получают систему
ур-ний, линейных по компонентам векторов
, получают систему
ур-ний, линейных по компонентам векторов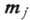 В отсутствие перем. внеш. магн. поля ур-ния однородны. Приравнивая детерминант
этой системы нулю, получают характеристич. ур-ние степени 2n относительно
частоты
В отсутствие перем. внеш. магн. поля ур-ния однородны. Приравнивая детерминант
этой системы нулю, получают характеристич. ур-ние степени 2n относительно
частоты 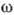 (п - число подрешёток). Если пренебречь затуханием, то значения корней характеристич.
ур-ния
(п - число подрешёток). Если пренебречь затуханием, то значения корней характеристич.
ур-ния 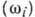 определяют
собств. частоты колебаний намагниченности подрешёток АФ.
определяют
собств. частоты колебаний намагниченности подрешёток АФ.
Каждой собств. частоте соответствует
своя мода колебаний - колебания набора определённых линейных комбинаций компонентов
векторов 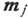 . Эти линейные
комбинации являются базисами неприводимых представлений группы магнитной
симметрии данного состояния АФ.
. Эти линейные
комбинации являются базисами неприводимых представлений группы магнитной
симметрии данного состояния АФ.
В общем случае для каждого значения
внеш. магн. поля 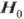 число собств. частот
число собств. частот 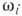 равно числу подрешёток в АФ. Две из этих частот стремятся к О при стремлении
к нулю энергии магнитной анизотропии и внеш. поля. Это т. н. релятивистские
моды. Остальные моды А. р. в АФ с числом подрешёток n>2 называют обменными.
Собств. частота обменной моды
равно числу подрешёток в АФ. Две из этих частот стремятся к О при стремлении
к нулю энергии магнитной анизотропии и внеш. поля. Это т. н. релятивистские
моды. Остальные моды А. р. в АФ с числом подрешёток n>2 называют обменными.
Собств. частота обменной моды 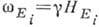 , где
, где 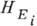 - эфф. обменное
поле, равное
- эфф. обменное
поле, равное
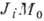 (
(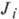 - линейная комбинация интегралов обменного взаимодействия между разл.
подрешётками,
- линейная комбинация интегралов обменного взаимодействия между разл.
подрешётками, 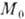 - намагниченность подрешёток). В случае релятивистских мод взаимные колебания
подрешёток отсутствуют или малы по сравнению с их колебаниями как целого. В
обменных модах основными являются взаимные колебания подрешёток. Обменные моды
А. р. можно возбудить эл--магн. полем только в том случае, если подрешётки в
АФ скошены в результате т. н. взаимодействия Дзялошинского (случай слабого антиферромагнетизма,
см. Слабый ферромагнетизм).
- намагниченность подрешёток). В случае релятивистских мод взаимные колебания
подрешёток отсутствуют или малы по сравнению с их колебаниями как целого. В
обменных модах основными являются взаимные колебания подрешёток. Обменные моды
А. р. можно возбудить эл--магн. полем только в том случае, если подрешётки в
АФ скошены в результате т. н. взаимодействия Дзялошинского (случай слабого антиферромагнетизма,
см. Слабый ферромагнетизм).
Для нахождения амплитуд вынужденных
колебаний в выражение для Ф следует добавить член 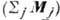 heiwt, учитывающий влияние перем. магн. поля. Решение линеаризованной системы ур-ний
(1) в этом случае даёт связь между амплитудой колебаний намагниченности
heiwt, учитывающий влияние перем. магн. поля. Решение линеаризованной системы ур-ний
(1) в этом случае даёт связь между амплитудой колебаний намагниченности
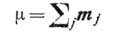 (3)
(3)
и амплитудой перем. поля h:
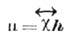 (4)
(4)
где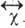 -тензор
магн. восприимчивости. Зависимость компонентов
-тензор
магн. восприимчивости. Зависимость компонентов 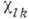 тензора от частоты имеет вид обычной кривой дисперсии. Знаменатель в выражении
тензора от частоты имеет вид обычной кривой дисперсии. Знаменатель в выражении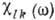 обращается в нуль при
обращается в нуль при 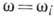 , если отсутствует затухание.
, если отсутствует затухание.
При учёте затухания можно выделить мнимую
часть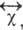 к-рая описывает поглощение эл--магн. энергии при А. р.
к-рая описывает поглощение эл--магн. энергии при А. р.
Ширина кривой поглощения 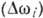 характеризует затухание. Член
характеризует затухание. Член 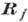 ,
описывающий затухание в ф-ле (1), можно представить в виде
,
описывающий затухание в ф-ле (1), можно представить в виде
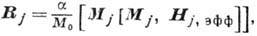 (5)
(5)
тогда
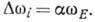 (6)
(6)
При одинаковых параметрах затухания
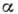 ширина линии в АФ значительно, в
ширина линии в АФ значительно, в 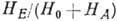 раз, больше, чем в ферромагнетике. Положение максимума кривой поглощения сдвигается
относительно
раз, больше, чем в ферромагнетике. Положение максимума кривой поглощения сдвигается
относительно 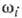 на
величину
на
величину 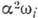 , к-рой
обычно пренебрегают и отождествляют частоты А. р. и собств. частоты АФ.
, к-рой
обычно пренебрегают и отождествляют частоты А. р. и собств. частоты АФ.
В качестве примера нахождения собств.
частот и мод колебаний А. р. рассмотрим одноосный двухподрешёточный АФ при T
= 0 К. Выражение для Ф удобнее записать, используя векторы антиферромагнетизма
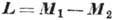 и намагниченности
и намагниченности
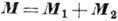 , компоненты к-рых
являются базисами неприводимых представлений двухподрешёточного А.:
, компоненты к-рых
являются базисами неприводимых представлений двухподрешёточного А.:
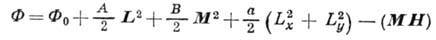 (7)
(7)
[квадратичный член (6/2) 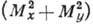 и члены высшего порядка для простоты не учитываются]. В дальнейшем принято,
что
и члены высшего порядка для простоты не учитываются]. В дальнейшем принято,
что 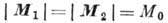 , тогда
, тогда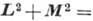
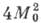 .
.
Осн. состояние АФ определяется путём
минимизации энергии Ф по 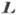 и
и 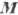 . Если а > О, то в осн. состоянии в отсутствие поля
. Если а > О, то в осн. состоянии в отсутствие поля 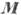 =
О, а вектор
=
О, а вектор 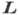 направлен
вдоль оси кристалла Oz. В магн. поле
направлен
вдоль оси кристалла Oz. В магн. поле 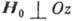 происходит небольшой скос подрешёток и
происходит небольшой скос подрешёток и 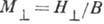 .
В магн. поле
.
В магн. поле 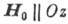 значение
M = О вплоть до поля Нс, при к-ром
происходит опрокидывание подрешёток (спин-флоп, см. Антиферромагнетизм:)
значение
M = О вплоть до поля Нс, при к-ром
происходит опрокидывание подрешёток (спин-флоп, см. Антиферромагнетизм:)
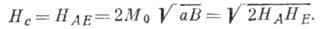 (8)
(8)
Здесь введены два эфф. поля - обменное
поле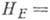
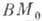 и поле анизотропии
и поле анизотропии 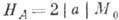 .
При
.
При 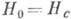 вектор L
устанавливается перпендикулярно Oz, возникает намагниченность
вектор L
устанавливается перпендикулярно Oz, возникает намагниченность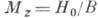 .
.
Замена в (1) векторов 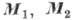 на
на 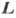 и
и 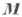 даёт систему из 6 ур-ний, решения к-рых пишутся в виде:
даёт систему из 6 ур-ний, решения к-рых пишутся в виде:
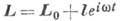 и
и 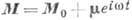 (9)
(9)
(значения 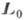 и
и 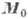 соответствуют осн. состоянию, a l и
соответствуют осн. состоянию, a l и 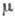 -амплитуды
колебании при А. р.).
-амплитуды
колебании при А. р.).
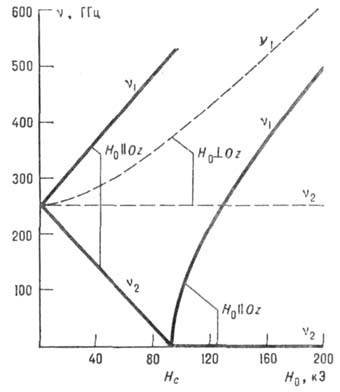
Рис. 1. Зависимость частоты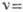
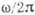 антиферромагнитного резонанса от магнитного поля
антиферромагнитного резонанса от магнитного поля 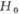 для легкоосного антиферромагнетика
для легкоосного антиферромагнетика 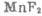 при Т = 4,2К и
при Т = 4,2К и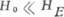 ,
,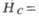
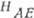 -
поле спин-флопа.
-
поле спин-флопа.
Собств. частоты 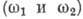 для перечисленных осн. состояний являются корнями характеристич. ур-ния системы
из 6 однородных ур-ний относительно
для перечисленных осн. состояний являются корнями характеристич. ур-ния системы
из 6 однородных ур-ний относительно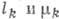
При 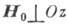 и
и 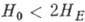 :
:
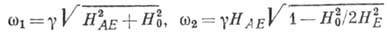 . (10)
. (10)
При 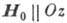 и
и 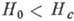 :
:
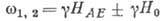 (11)
(11)
При 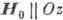 и
и 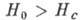 :
:
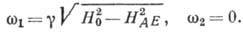 (12)
(12)
В поле 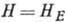 происходит схлопывание подрешёток (спин-флип). В больших полях резонанс наблюдается
на одной частоте:
происходит схлопывание подрешёток (спин-флип). В больших полях резонанс наблюдается
на одной частоте: 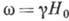 (в приближении
(в приближении 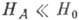 ).
Зависимость собств. частот от магн. поля показана на рис. 1.
).
Зависимость собств. частот от магн. поля показана на рис. 1.
На рис. 2 показан вид свободных колебаний
векторов  (относит.
величина M сильно завышена) в легкоосном АФ при Н =0. Характерной
особенностью прецессии векторов намагниченности подрешёток в этом случае является
тот факт, что даже в отсутствие внеш. магн. поля подрешётки скашиваются и возникает
намагниченность т, к-рая прецессирует (в фазе или в противофазе
с L), оставаясь всё время перпендикулярной вектору L. Возникающий при свободных колебаниях скос подрешёток объясняет появление
обменного поля
(относит.
величина M сильно завышена) в легкоосном АФ при Н =0. Характерной
особенностью прецессии векторов намагниченности подрешёток в этом случае является
тот факт, что даже в отсутствие внеш. магн. поля подрешётки скашиваются и возникает
намагниченность т, к-рая прецессирует (в фазе или в противофазе
с L), оставаясь всё время перпендикулярной вектору L. Возникающий при свободных колебаниях скос подрешёток объясняет появление
обменного поля 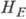 в
ф-лах для собств. частот. Как видно из рис. 2, две моды колебаний отличаются
направлением прецессии векторов L и M и проекций
вектора т на ось Oz. Эта проекция и обусловливает, как видно из
ф-лы (6), снятие вырождения при наложении магн. поля вдоль оси Oz. Круговая
прецессия векторов намагниченности наблюдается только в легкоосном АФ (в слабом
поле
в
ф-лах для собств. частот. Как видно из рис. 2, две моды колебаний отличаются
направлением прецессии векторов L и M и проекций
вектора т на ось Oz. Эта проекция и обусловливает, как видно из
ф-лы (6), снятие вырождения при наложении магн. поля вдоль оси Oz. Круговая
прецессия векторов намагниченности наблюдается только в легкоосном АФ (в слабом
поле 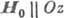 ). В большинстве
случаев колебания векторов L и M носят более сложный
характер.
). В большинстве
случаев колебания векторов L и M носят более сложный
характер.
Для АФ типа "лёгкая плоскость"
(у них в осн. состоянии вектор L, лежит в базисной плоскости)
значение параметра а в (7) отрицательно (а < О). В поле
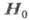 любого направления
вектор L, устанавливается перпендикулярно
любого направления
вектор L, устанавливается перпендикулярно 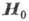 (в пренебрежение анизотропией в базисной плоскости) и намагниченность
(в пренебрежение анизотропией в базисной плоскости) и намагниченность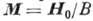 Собств. частоты свободных колебаний:
Собств. частоты свободных колебаний:
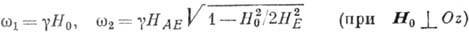 (13)
(13)
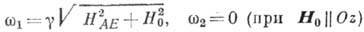 . (14)
. (14)
В легкоплоскостных АФ со слабым ферромагнетизмом
в ф-лы для А. р. входит поле Дзялошинского 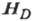 .
.
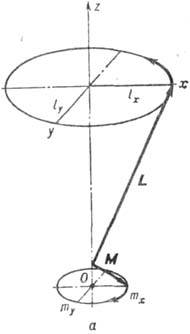
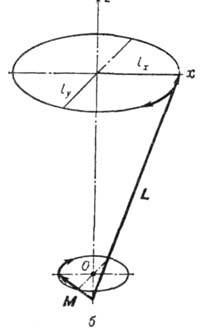
Рис. 2. Прецессия векторов L
и M при антиферромагнитном резонансе в легкоосном антиферромагнетике:
а - мода с большей частотой [знак + в формуле (11)]: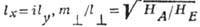 ; б-мода с меньшей частотой
; б-мода с меньшей частотой 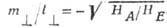 [знак - в формуле (11)]:
[знак - в формуле (11)]: 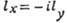 .
.
В частности, в ромбоэдрич. АФ со слабым ферромагнетизмом
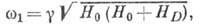
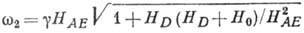 (15)
(15)
Спектр А. р. для легкоплоскостных АФ
со слабым ферромагнетизмом приведён на рис. 3. Схема колебаний векторов M
и L для HЧ-ветви показана на рис. 4.
Наличие безактивац. ветви А. р. 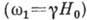 у легкоплоскостного АФ обусловлено общим св-вом систем со
спонтанно нарушенной симметрией (теорема Голдстоуна).
у легкоплоскостного АФ обусловлено общим св-вом систем со
спонтанно нарушенной симметрией (теорема Голдстоуна).
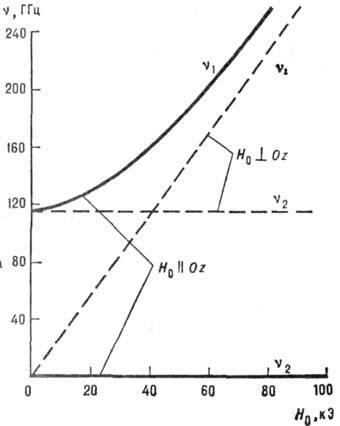
Рис. 3. Зависимость частоты 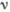 антиферромагнитного резонанса от магнитного поля для легкоплоскостного антиферромагнетика
антиферромагнитного резонанса от магнитного поля для легкоплоскостного антиферромагнетика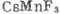 при Т=4,2 К и
при Т=4,2 К и 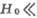
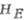 (без учёта сверхтонкого взаимодействия).
(без учёта сверхтонкого взаимодействия).
Установление упорядоченного состояния в легкоплоскостном АФ приводит к спонтанному нарушению симметрии - в изотропной базисной плоскости появляется выделенное направление - направление вектора антиферромагнетизма L. Однако это направление ничем не зафиксировано, и вращение вектора L в плоскости не влияет на энергию АФ.
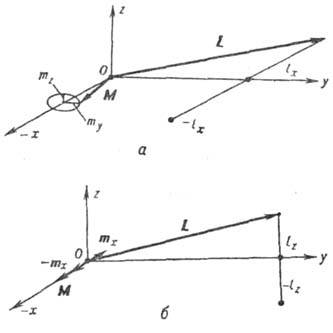
Рис. 4. Колебания векторов L и
M при антиферромагиитном резонансе в легкоплоскостном антиферромагнетике
со слабым ферромагнетизмом: а - низкочастотная мода,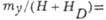
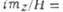
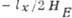 б -высокочастотная мода,
б -высокочастотная мода,
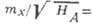
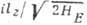 .
.
Поэтому частота колебаний в плоскости
должна обращаться в нуль в отсутствие внеш. поля. Это же наблюдается и в состоянии
с опрокинутыми подрешётками [в спин-флоп фазе, ф-ла (2)].
Учёт любого слабого (по сравнению с 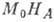 и
и 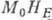 )
взаимодействия, фиксирующего направление вектора L, в базисной
плоскости, приводит к появлению щели в спектре А. р. и вместо
)
взаимодействия, фиксирующего направление вектора L, в базисной
плоскости, приводит к появлению щели в спектре А. р. и вместо 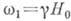 ф-ла для резонансной частоты принимает вид
ф-ла для резонансной частоты принимает вид
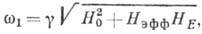 (16)
(16)
где поле 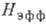 обусловлено разл. процессами, происходящими в кристалле при установлении в нём
магн. упорядочения. Пока изучены два источника возникновения
обусловлено разл. процессами, происходящими в кристалле при установлении в нём
магн. упорядочения. Пока изучены два источника возникновения 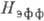 -спонтанная
стрикция и упорядочение ядерных магн. моментов под действием сверхтонкого взаимодействия.
Возникающее в результате спонтанной стрикции поле
-спонтанная
стрикция и упорядочение ядерных магн. моментов под действием сверхтонкого взаимодействия.
Возникающее в результате спонтанной стрикции поле 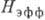 для ромбоэдрич. кристаллов может быть выражено через модули упругости
для ромбоэдрич. кристаллов может быть выражено через модули упругости 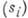 и константы магнитострикции
и константы магнитострикции 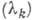 :
:
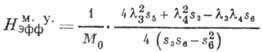 (17)
(17)
Хотя величина магнитоупругого поля 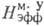 мала (~1 Э), его действие, усиленное полем HЕ, приводит к
заметной щели в спектре А. р. для ряда АФ. Напр., в гематите
мала (~1 Э), его действие, усиленное полем HЕ, приводит к
заметной щели в спектре А. р. для ряда АФ. Напр., в гематите 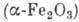 щель
щель 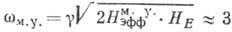 ГГц. Возникающее
в результате сверхтонкого взаимодействия поле
ГГц. Возникающее
в результате сверхтонкого взаимодействия поле
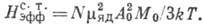 (18)
(18)
Здесь N - число магн. ионов в
1 см3, 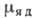 - ядерный магн. момент, A0 - безразмерная константа сверхтонкого
взаимодействия. Эффект сверхтонкого взаимодействия проявляется при низких темп-pax.
Для иона
- ядерный магн. момент, A0 - безразмерная константа сверхтонкого
взаимодействия. Эффект сверхтонкого взаимодействия проявляется при низких темп-pax.
Для иона 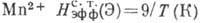 и при
Т=4 К в соединениях
и при
Т=4 К в соединениях 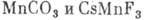 щель в спектре, возникающая в результате сверхтонкого взаимодействия, эквивалентна
действию магн. поля y1
кЭ и составляет y3
ГГц.
щель в спектре, возникающая в результате сверхтонкого взаимодействия, эквивалентна
действию магн. поля y1
кЭ и составляет y3
ГГц.
В кубич. АФ встречаются в осн. два типа
магн. структур. В структуре первого типа вектор L направлен вдоль
кристаллографич. оси [100]. В этом случае в поле (1-5) кЭ, направленном вдоль
оси [100], векторы намагниченности подрешёток устанавливаются перпендикулярно
приложенному полю, и спектр А. р. подобен тому, к-рый наблюдается в опрокинутом
легкоосном АФ. В слабых полях образец бывает разбит на 90° T-домены
(см. Антиферромагнитные домены)и наблюдается неск. линий А. р. В структуре
2-го типа вектор L лежит в одной из четырёх плоскостей типа (111). B
этом случае с помощью магн. поля невозможно уничтожить T-домены и перевести
АФ в однодоменное состояние. В любых полях, меньших поля схлопывания подрешёток
(спин-флипа), наблюдается неск. линий А. р. со сложной зависимостью их резонансных
полей от угла между полем и кристаллографич. осями образца. Все линии от разных
Т-доменов сливаются в одну, когда 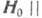 [100].
[100].
В орторомбич. АФ и кристаллах с более
низкой симметрией наблюдаются две щели в спектре А. р. У них в отсутствие внеш.
магн. поля наблюдаются две частоты А. р.: 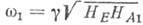 и
и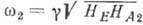 , где
, где 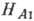 и
и 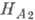 - поля анизотропии
относительно оси лёгкого намагничивания и оси, следующей за ней по значению
энергии анизотропии.
- поля анизотропии
относительно оси лёгкого намагничивания и оси, следующей за ней по значению
энергии анизотропии.
Обычно 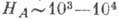 Э (кроме кубич. кристаллов), а обменные поля
Э (кроме кубич. кристаллов), а обменные поля 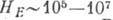 Э. Поэтому частоты А. р. изменяются от 10 до сотен ГГц. Однако есть много АФ,
в к-рых значения
Э. Поэтому частоты А. р. изменяются от 10 до сотен ГГц. Однако есть много АФ,
в к-рых значения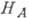 и
и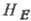 на
порядок больше. Частоты А. р. приходятся в этом случае на область далёкого ИК-диапазона,
где их не всегда можно отличить от др. типов возбуждений.
на
порядок больше. Частоты А. р. приходятся в этом случае на область далёкого ИК-диапазона,
где их не всегда можно отличить от др. типов возбуждений.
Изучение спектров А. р. в достаточно
широкой области частот и магн. полой даёт обширную информацию о магн. структуре,
величинах обменного, анизотропного, сверхтонкого, магнитоупругого и др. видов
взаимодействия в антиферромагнетиках, а также о температурной зависимости этих
взаимодействий. Изучение ширины линии А. р. в принципе позволяет раскрыть природу
процессов релаксации магнонов в АФ.
Для наблюдения А. р. используются радиоспектрометры,
аналогичные применяемым для изучения ЭПР, но позволяющие проводить измерения
на высоких (до 1000 ГГц) частотах и в сильных (до 1 МГс) магн. полях. Наиболее
перспективны спектрометры, в к-рых сканируется не магн. поле, а частота. Получили
распространение оптич. методы детектирования А. р.

А. С. Боровик-Романов.
Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта").
Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|