Нелинейная акустика. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Нелинейная акустика - область акустики, в к-рой изучают явления в звуковых полях большой интенсивности и взаимодействия звуковых волн с возмущениями другой природы (гидродинамич., тепловыми, эл--магн. и т. д.). Для описания этих явлений недостаточны приближения линейной теории звука и необходим учёт нелинейных членов ур-ний гидродинамики и ур-ния состояния. Такие явления (т. н. нелинейные эффекты) возникают в результате изменения физ. свойств среды, вызванных распространяющейся волной большой интенсивности и влияющих как на условия распространения данной волны (самовоздействие), так и на др. виды возмущений (взаимодействие).

Развитие H. а. стимулировалось применением интенсивных звуковых полей и связанных с ними нелинейных эффектов. Так, необходимость увеличения интенсивности акустич. волн, используемых в УЗ-технологии, потребовала изучения условий фокусировки мощного звука и усреднённых эффектов в звуковых полях; совершенствование техн. средств, применяемых для зондирования океана и атмосферы, привело к разработке параметрич. приёмных и излучающих систем. Увеличение мощности индустриальных шумов, в особенности уровня авиац. шумов, потребовало разработки теории генерации звука турбулентностью и изучения особенностей распространения шума большой интенсивности.

Нелинейная акустика занимает промежуточное место между линейной теорией звука и теорией ударных волн. Предметом её исследований являются слабо нелинейные волны, в то время как ударные волны, как правило, сильно нелинейны; в классич. же акустике нелинейные эффекты не рассматриваются вообще. H. а. близка к нелинейной оптике и др. разделам физики нелинейных волн. К осн. вопросам, к-рыми занимается совр. H. а., относятся: распространение волн конечной амплитуды, звуковые пучки большой интенсивности и их самовоздействие, нелинейное поглощение и взаимодействие волн, особенности нелинейного взаимодействия в твёрдых телах, генерация и распространение интенсивных шумов, усреднённые эффекты в звуковом поле, акустич. кавитация и др.

Распространение волны конечной амплитуды

Распространение звуковой волны большой интенсивности (т. н. волны конечной амплитуды), в отличие от малоамплитудной, сопровождается нарастающим искажением её формы, обусловленным разницей в скоростях перемещения разл. точек профиля волны. Скорость с перемещения точки профиля, соответствующей заданному значению колебат. скорости u, определяется ф-лой

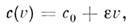
где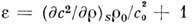

- нелинейный параметр среды, r₀ и c₀ - равновесные значения плотности среды и скорости звука в ней, S - энтропия. Точки профиля волны, соответствующие областям сжатия (где u > 0), "бегут" быстрее точек, соответствующих областям разрежения (где u < 0), т. к. скорость звука в области сжатия больше, чем в области разрежения. Кроме того, происходит увлечение волны средой, к-рая в области сжатия движется в направлении распространения волны, а в области разрежения - в противоположную сторону. Разница скоростей для разл. точек профиля пренебрежимо мала в случае волн малой интенсивности, и волна успевает затухнуть, прежде чем в ней разовьются нелинейные эффекты. Поэтому распространение таких волн происходит практически без изменения формы, в соответствии с соотношениями линейной акустики, согласно к-рой скорость звука для всех точек профиля волны постоянна. Если же интенсивность волны достаточно велика, то влияние нелинейных эффектов оказывается более сильным, чем влияние диссипативных процессов, обусловливающих затухание волны, и крутизна волновых фронтов по мере распространения возрастает.

Для матем. описания явлений в звуковых полях большой интенсивности необходим учёт нелинейных членов ур-ний механики сплошной среды. В частности, следует принять во внимание, что при больших возмущениях избыточное давление р' уже не пропорц. избыточной плотности r' (нелинейность Гука закона для случая твёрдых тел), а выражается соотношением

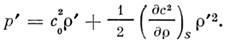
Кроме того, следует учесть нелинейные члены ур-ний движения сплошной среды. В результате получаются нелинейные ур-ния, к-рые для простейшего случая распространения плоской волны могут быть сведены к одному ур-нию (ур-нию Бюргерса):

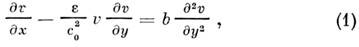
где x - координата, вдоль к-рой распространяется волна, у = t - x/c₀, t - время, b = v_эф/2c³₀ - диссипативный параметр среды. Здесь v_эф = r^-1₀[h + z +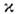

(c^-1_v - c^-1_p ) - эффективная кинематич. вязкость, h и z - коэф. сдвиговой и объёмной вязкостей,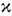

- коэф. теплопроводности, c_v и с_р - уд. теплоёмкости при постоянном объёме и давлении.

Вклад нелинейных эффектов зависит от амплитуды волны и характеризуется акустич. Маха числом: М_а = u_m/c₀ = r'_m/r₀ (где u_m - амплитуда колебат. скорости частиц, r'_m - вызванная звуковым возмущением амплитуда избыточной плотности), имеющим порядок отношения нелинейного члена к линейному в ур-нии (1). Относит. роль нелинейных и диссипативных аффектов характеризуется акустич. Рейнольдса числом Re_a = eu_m₀l/pv_эф (где u_т₀ - нач. значение амплитуды колебат. скорости, l = c₀/f - длина звуковой волны, f = w/2p - её частота) определяет отношение нелинейного члена к диссипативному в ур-нии (1). Для воды Re_a = 3p_m/f, где р_т - амплитуда звукового давления в MПa, f - в МГц, поэтому для наблюдения нелинейного эффекта на УЗ-частотах ~1 МГц должно быть р_т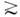

1 МПа. При Re_a >> 1 искажения формы волны становятся столь сильными, что образуется пилообразная волна (рис. 1). Профиль одного периода волны описывается точным решением ур-ния (1)

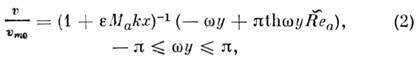
где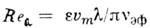

- текущее значение акустич. числа Рейнольдса, u_m=u_m₀ (1 + eM_akx), k - волновое число, w - частота первоначальной гармонич. волны.

Пилообразную волну можно рассматривать как ударную волну, толщина сжатия к-рой, согласно (2), определяется ф-лой d/l

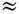(2Re_a)^-1. На начальной стадии образования пилообразной волны, когда

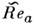= Re_a >> 1, d/l << 1 и величину d можно представить в виде d =v_эф/eu_m₀, что совпадает с выражением для толщины фронта слабой стационарной ударной волны со с качком скорости u_m₀.

Расстояние L, на к-ром происходит существенное изменение формы волны, зависит от амплитуды и длины звуковой волны. Для плоской волны оно определяется ф-лой kL = eМ_а. Так, в воде для волны интенсивностью в неск. десятков Вт/см² L - порядка сотни длин волн (рис.2). В расходящихся (напр., сферич. или цилиндрич.) волнах эффект проявляется слабее, а в сходящихся сильнее, чем в плоских. В стоячих волнах конечной амплитуды также могут возникать ударные волны, причём их фронты движутся, периодически отражаясь от границ объёма, в к-ром возбуждена стоячая волна.

Рис. 2. Осциллограмма профиля волны конечной амплитуды на расстоянии 100 длин волн от излучателя. Амплитуда давления 1 МПа, частота 0,775 МГц.

Со спектр. точки зрения искажение формы волны означает нарастание в её спектре высших гармонич. составляющих осн. частоты. Их амплитуда вначале нарастает, достигает максимума в области наиб. искажения волны при x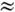

L и затем убывает вновь. В области, где d

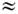l, волна становится снова синусоидальной.

Нелинейное поглощение звука

Увеличение крутизны волновых фронтов приводит к увеличению градиентов скорости и температуры, что сопровождается сильной диссипацией энергии и является причиной нелинейного поглощения звука. Со спектр. точки зрения этот процесс можно рассматривать так же, как результат перекачки энергии в высшие, более сильно поглощающиеся гармонич. составляющие волны. Поскольку форма волны при распространении меняется, коэф. её поглощения также зависит от расстояния: вблизи излучателя для первоначально синусоидальной волны поглощение невелико и описывается обычными выражениями линейной акустики (см. Поглощение звука; )при удалении от излучателя коэф. поглощения возрастает, достигая максимума в области наиб. искажений волны, после чего убывает. Поглощение в данной точке пространства зависит от амплитуды волны, возрастая с её увеличением.

Амплитудный коэф. поглощения первой гармоники волны, a'₁, в области пилообразной волны определяется ф-лой

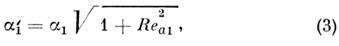
где a₁ = v_эфw²/2с³₀- коэф. поглощения малоамплитудной волны (рис. 3). Напр., при распространении в воде УЗ-волны с амплитудой звукового давления p_m = 0,3 Па и частотой w = 10⁷ с^-1 в области образования пилообразной волны Re_a = 10² и коэф. поглощения a₁' возрастает на два порядка по сравнению c a₁.

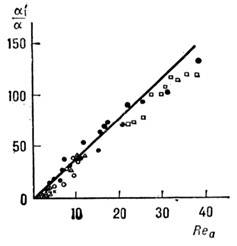
Рис. 3. Зависимость относительного коэффициента поглощения волны конечной амплитуды от акустического числа Рейнольдса. Сплошная линия-результат расчёта по формуле (3), значки - экспериментальные данные.

Поглощение волн большой интенсивности происходит по неэкспоненц. закону. Уменьшение пикового значения колебат. скорости u_п плоской пилообразной волны описывается ф-лой

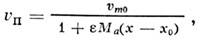
где u_m₀ = u_m(x₀). Рост поглощения волны с увеличением её интенсивности приводит к явлению насыщения: при постепенном увеличении интенсивности излучения амплитуда звука в фиксир. точке ноля растёт всё медленнее, асимптотически приближаясь к предельному значению, не зависящему от нач. амплитуды. Эффект нелинейного поглощения звука может заметно проявиться в мощных УЗ-фокусирующих системах, приводя к снижению коэф. усиления (см. Фокусировка звука).

Звуковые пучки большой интенсивности

В звуковых пучках высокой интенсивности изменение формы волны при распространении происходит не только вследствие различия в скоростях перемещения разл. точек профиля волны, но и в результате дифракц. эффектов. Если расстояние l от излучателя звука до области образования волны не выходит за пределы ближней зоны (см. Звуковое поле ),т. е. l меньше длины т. н. прожекторной зоны излучателя: l < ka²/2 (где a - радиус излучателя), то в области, где волна остаётся плоской, из синусоидальной волны успевает образоваться пилообразная волна, к-рая затем в результате сферич. расхождения в дальней зоне преобразуется в периодич. последовательность импульсов (рис. 4).

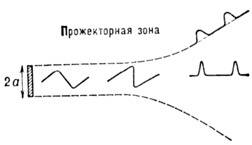
Рис. 4. Схема эволюции профиля волны в интенсивном УЗ-пучке.

Если же интенсивность волны недостаточно велика и пилообразная волна не успевает образоваться в прожекторной зоне излучателя, то вначале развиваются дифракц. эффекты сферич. расхождения и лишь в дальней зоне, в расходящейся волне происходит увеличение крутизны профиля волны с расстоянием по логарифмич. закону.

По мере распространения волны происходит перераспределение её интенсивности по сечению пучка, что чаще всего обусловлено нелинейным поглощением. Так, при распространении остронаправленного пучка с убывающей по радиусу пучка интенсивностью амплитудное распределение выравнивается по сечению вследствие более сильного поглощения волны в области больших амплитуд. Изменение распределения интенсивности звука по сечению пучка может быть вызвано также процессами самофокусировки или самодефокусировки. При распространении звука в жидкости эти процессы обычно обусловлены локальным изменением скорости звука в результате нагревания среды, вызванного диссипацией акустич. энергии. Вблизи оси пучка интенсивность звука больше и соответственно среда сильнее разогревается. Если при этом скорость звука с ростом температуры падает, то происходит самофокусировка; напротив, если скорость звука растёт с увеличением температуры, пучок дефокусируется. Дефокусирующее влияние оказывают также акустические течения ,развивающиеся в поле мощного пучка и приводящие к добавочному переносу звуковой волны вблизи оси пучка.

Разнообразны механизмы самовоздействия звука в жидкостях с пузырьками газа. Появление пузырьков приводит к снижению скорости звука. Если их распределение по сечению пучка неравномерно и концентрация пузырьков в приосевой области более высока, что может быть связано, напр., с развитием кавитации, то скорость звука в центр. части пучка снижается и пучок фокусируется. Процесс самовоздействия звука может развиться и при равномерном распределении пузырьков в жидкости, т. к. вследствие сильной нелинейности такой среды в ней наблюдается не только различие в скоростях перемещения разных точек профиля волны, но и скорость переноса волны как целого оказывается зависящей от амплитуды. Это приводит, в силу неравномерности распределения амплитуды звука по радиусу пучка, к самофокусировке (если скорость звука падает с ростом амплитуды) или к самодефокусировке (в обратном случае).

Ряд эффектов связан с трансляц. движением пузырьков. К их числу относится эффект нелинейного просветления пузырьковой среды, заключающийся в сильном уменьшении поглощения звука в пузырьковой среде по мере увеличения интенсивности акустич. волны. Это происходит вследствие того, что пульсирующие в звуковом поле пузырьки сближаются и сливаются, что приводит к уменьшению числа резонансных пузырьков, диссипирующих звуковую энергию, и поглощение среды уменьшается.

Нелинейное взаимодействие звуковых волн

При возбуждении в среде одновременно неск. волн большой интенсивности они не распространяются независимо, а порождают новые волны, т. н. комбинационные тона ,частоты к-рых равны сумме и разности частот первичных волн. Наиб. выражены комбинац. тона, отвечающие резонансному взаимодействию волн, возникающему при выполнении условий синхронизма:

где w и k - частота и волновой вектор волны комбинац. тона, w', w'' и k', k'' - частоты и волновые векторы первичных волн. Амплитуда волны комбинац. тона A_k при резонансном взаимодействии описывается ур-нием

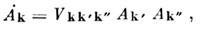
где V_kk_'_k_'' - потенциал взаимодействия, определяемый характером нелинейности среды, A_k_', A_k_'' - амплитуды исходных волн. В приближении заданного поля (A_k_' = const, A_k_'' = const) это ур-ние приводит к линейно нарастающей со временем амплитуде A_k. Это значит, что по мере распространения волны происходит нарастание комбинац. тона до тех пор, пока влияние поглощения или ослабления первичных волн из-за перекачки энергии в комбинац. тона не замедлит этот процесс. Если условия синхронизма не выполняются и имеется расфазировка, интенсивность комбинац. тона не нарастает, а меняется периодически по мере распространения волны.

Эффект генерации комбинац. тона в среде при взаимодействии звуковых пучков разл. частоты лежит в основе работы т. н. параметрических излучателей и приёмников звука, в к-рых область взаимодействия первичных волн (наз. волнами накачки) играет роль "бестелесной" антенны.

При распространении звука в жидкостях и газах влияние дисперсии чаще всего не существенно и все коллинеарно распространяющиеся волны оказываются в резонансе. Если же дисперсия скорости звука существенна, как, напр., в жидкости с пузырьками газа или в нек-рых твёрдых телах, то для определения условий резонансного взаимодействия пользуются методом дисперсионнных диаграмм. 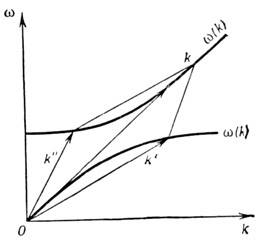В простейшем случае коллинеарного взаимодействия волн для каждой из них строится дисперсионная характеристика w_i(k_i) (где i = 1, 2, 3), к-рая представляет кривую (рис. 5) (или прямую - при отсутствии дисперсии). Наклон вектора, проведённого из начала координат О в точку, лежащую на дисперсионной характеристике, определяет фазовую скорость волны с данной частотой. Каждой из взаимодействующих волн ставится в соответствие

Рис. 5. Дисперсионная диаграмма трёхволнового кол-линеарного взаимодействия звуковых волн в жидкости с пузырьками газа. Кривые изображают две ветви дисперсионной зависимости w( k).

вектор с компонентами (w_i, k_i). При выполнении условий синхронизма (4) необходимо, чтобы вектор, соответствующий третьей компоненте взаимодействующих волн, представлял собой сумму векторов, отвечающих двум другим компонентам триплета, т. е. чтобы три вектора, вершины к-рых лежат на дисперсионной кривой, образовали треугольник.

Если точного сложения векторов не происходит, то считается, что условия синхронизма выполняются приближённо и в условия (4) вводится расстройка по волновому вектору Dk или по частоте Dw:

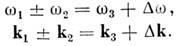
Наличие расстройки приводит к пространственным или временным биениям результирующей волны. Если дисперсия отсутствует и все волны распространяются с одинаковой скоростью, то резонансные условия выполняются только для коллинеарного взаимодействия, что характерно для большинства жидкостей и газов. В изотропных твёрдых телах скорости продольных и сдвиговых волн различны, что открывает возможность выполнения условий синхронизма и для волн, распространяющихся под углом друг к другу (рис. 6).

Взаимодействие звука с "незвуковыми" возмущениями среды - с температурными волнами, а в жидкости с капиллярными волнами и пузырьками газа - может приводить к явлению вынужденного рассеяния звука, подобного вынужденному Мандельштама - Бриллюэ-на рассеянию в оптике. Звук, рассеиваясь на возмущении среды и взаимодействуя с ним, увеличивает амплитуду возмущения, что в свою очередь приводит к ещё более сильному рассеянию звука.

Если интенсивность одной из взаимодействующих волн во много раз больше интенсивности другой волны, то можно пренебречь обратным воздействием слабой волны на сильную и рассматривать воздействие интенсивной волны (волны накачки) как фактор, изменяющий

параметры среды, в к-рой распространяется слабая (сигнальная) волна. Перекачка энергии от сильной волны к слабой лежит в основе работы параметрич. усилителей и генераторов, применяемых в оптике. В акустике осн. трудность при создании параметрич. усилителей звука связана с тем, что из-за слабой дисперсии звуковых волн первичная волна накачки обычно быстро затухает в результате генерации ВЧ-гармоник, не успев передать энергию в сигнальную волну. Для преодоления этой трудности специально создаются нелинейные системы с дисперсией. Один из примеров такой системы - акустич. резонатор в виде полого кольца (тора), в одном из сечений к-рого помещён ВЧ-излуча-тель накачки. Наличие волноводной дисперсии позволяет осуществить в такой системе параметрич. усиление и генерацию НЧ-звука. Другая возможность - использование дисперсии в самом веществе путём выбора специальных сред и соответствующих частот. Например, параметрическое усиление звука в поле высокочастотной УЗ-накачки наблюдалось в кристаллах окиси магния.

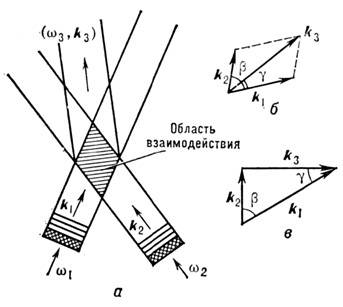
Рис. 6. Область взаимодействия при неколлинеар-ном взаимодействии волн (а) и образование волн суммарной (б) и разностной (в) частот.

Режимы параметрич. усиления могут осуществляться и при взаимодействии звука с др. видами возмущений среды. Так, в пьезополупроводнике, помещённом в элек-трич. ноле, имеет место параметрич. усиление звука за счёт дрейфа электронов в приложенном электрич. поле и обратного пьезоэффекта.

Особенности нелинейного взаимодействия в твёрдых телах

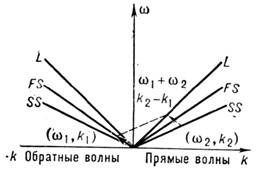
В отличие от газов и жидкостей, в твёрдых телах вдоль произвольного направления могут распространяться (в общем случае) три упругие волны с разл. фазовыми скоростями и со взаимно ортогональными направлениями колебаний частиц среды (см. Кристаллоакустика ).Это увеличивает число видов взаимодействия акустич. волн, разрешённых условиями фазового синхронизма (4). В твёрдом теле оказывается возможным, в частности, резонансное взаимодействие встречных волн, отсутствующее в жидкостях и газах. Напр., в изотропном твёрдом теле коллинеарно распространяющиеся встречные быстрая (FT)и медленная (ST)поперечные волны с частотами w₁ и w₂образуют резонансный триплет с продольной волной (L)суммарной частоты (рис. 7) при след. соотношении частот:

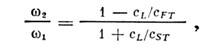
где c_L, c_FT, c_ST. - скорости соответствующих волн. Резонансные триплеты могут образовывать также волны, распространяющиеся под углом друг к другу. Напр., резонансное возбуждение продольной волны суммарной частоты поперечными волнами, пересекающимися под углом b, происходит при выполнении условия

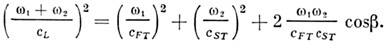
В изотропном твёрдом теле пересекающиеся под углом волны могут образовать пять видов резонансных триплетов, в анизотропных телах (кристаллах) их число возрастает до 21. В кристаллах, кроме того, появляется зависимость эффективности взаимодействия от ориен-

Рис. 7. Дисперсионная диаграмма встречного колли-неарного взаимодействия бездисперсионных акустических волн: быстрой сдвиговой FT и медленной сдвиговой ST с образованием продольной волны L суммарной частоты.

тации волновых векторов взаимодействующих волн относительно кристаллографич. осей. При этом генерация комбинац. тонов для поперечных волн может происходить с поворотом плоскости поляризации волны.

Взаимодействия волн в твёрдых телах обусловлены обычно нелинейностью упругих возмущений, описываемых нелинейными ур-ниями механики сплошной среды. Возможны также механизмы нелинейности, связанные с взаимодействием упругих деформаций с др. видами возбуждений в твёрдом теле. В пьезоэлектрич. кристаллах может проявиться нелинейность пьезоэффекта; в пьезополупроводниках доминирующим механизмом часто оказывается электронная (концентрационная) нелинейность, обусловленная нелинейной зависимостью концентрации носителей заряда от деформации, вызванной акустич. волной. Соответственно, если при экс-перим. исследовании нелинейных искажений УЗ-вол-ны в большинстве твёрдых тел при частотах в неск. МГц и амплитудах деформации ~10^-5 величина второй гармоники не превышает неск. % от амплитуды первой гармоники, то в пьезополупроводниковых кристаллах, благодаря вкладу акустоэлектронной нелинейности, она возрастает более чем на порядок.

В пьезоэлектрич. кристаллах акустич. волны могут взаимодействовать не только между собой, но и с эл--магн. волнами, в частном случае - с однородным электрич. или магн. полем. Напр., встречное взаимодействие бегущих акустич. волн одинаковой поляризации в пьезоэлектрич. кристалле приводит к возбуждению однородного электрич. поля удвоенной частоты. Этот эффект используется в устройствах обработки сигналов в акустоэлектронике.

При излучении в пьезоэлектрич. образец одной акустич. волны и одноврем. возбуждении электрич. поля на удвоенной частоте наблюдается параметрич. генерация встречной акустич. волны - третьей компоненты рассматриваемого резонансного триплета, образованного двумя встречными акустич. волнами и электрич. полем. Описанные эффекты взаимодействия акустич. волн и переменного электрич. поля лежат в основе электроакустического эха и являются одним из примеров обращения волнового фронта.

Нелинейные взаимодействия приводят к изменению параметров акустич. волны под влиянием постоянных или медленно меняющихся механич. или электрич. полей. При механич. деформировании кристаллов, напр., изменяются фазовая и групповая скорости акустич. волн и их поляризация. В пьезоэлектрич. кристаллах фазовая скорость акустич. волн изменяется также при приложении постоянных электрич. полей. Указанные эффекты используются для измерения внутр. напряжений, определения модулей упругости третьего и более высоких порядков, управления акустич. волнами.

Исследование нелинейных взаимодействий УЗ-волн в твёрдых телах важно для определения характеристик фонон-фононных взаимодействий, лежащих в основе процессов установления теплового равновесия, теплопроводности, теплового расширения твёрдых тел.

Фонон-фононные взаимодействия играют определяющую роль в поглощении гиперзвуковых волн (см. Гиперзвук)в кристаллах, особенно при низких температурах, в эффектах нелинейного поглощения УЗ-волн.

Шумы большой интенсивности

Распространение шумов большой интенсивности отличается от поведения слабого шума. В процессе распространения спектр шума меняется: спектр. плотность его в области высоких частот растёт в результате генерации гармоник энергонесущих спектр. компонент, расширяется и НЧ-часть спектра из-за появления комбинац. ионов при условии, что максимум спектр. плотности шума в нач. момент соответствовал частоте, отличной от нулевой. На расстояниях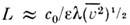

(где l - длина волны энергонесущей компоненты,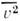

- среднеквадратичная коле-бат. скорость) в шумовом сигнале возникают разрывы и затухание шума растёт. На этой стадии в ВЧ-обла-сти спектра спектр. плотность шума спадает по универсальному закону w^-4, не зависящему от вида нач. спектра. Генерация интенсивных шумов часто также бывает связана с нелинейными взаимодействиями гид-родинамич. возмущений. Напр., шумы самолётных и ракетных двигателей в значит. степени обусловлены генерацией шума, турбулентностью в результате вихревых взаимодействий (см. Аэроакустика).

Усреднённые эффекты в звуковом поле. Кавитация

В звуковых полях большой интенсивности наряду с переменными возмущениями среды, меняющимися с частотой звука, могут возникать постоянные силы и скорости, пропорц. квадрату амплитуды звука. Они обусловливают т. н. усреднённые эффекты в звуковом поле, к числу к-рых относятся давление звукового излучения, акустические течения, воздействие на помещённые в звуковом поле тела (см. Пондеромоторные силы в звуковом поле) и др.

В жидкости распространение интенсивных звуковых волн может вызывать акустич. кавитацию - появление в сплошной среде интенсивно пульсирующих полостей, сопровождающееся излучением мощных акустич. импульсов сжатия и возникновением микропотоков вблизи пузырьков. С физ. точки зрения кавитацию можно рассматривать как процесс кумуляции энергии, плотность к-рой в окрестности пузырька превышает среднюю плотность анергии акустич. поля в 10³-10⁴ раз.

Применение нелинейных акустических эффектов

Первые применения нелинейных эффектов были связаны с разработкой методов измерения характеристик акустич. поля на основе регистрации усреднённых эффектов: измерение интенсивности звука по давлению звукового излучения с помощью радиометров или по вспучиванию свободной поверхности жидкости под действием звука, измерение колебат. скорости методом Рэлея диска .Для зондирования атмосферы, океана, для целей медицинской акустики применяют параметрические излучатели и приёмники благодаря их широкополосности, острой направленности излучения и отсутствию боковых лепестков в диаграмме направленности.

Многие процессы УЗ-технологии базируются на использовании нелинейных эффектов. В установках УЗ-очистки поверхностей деталей кавитац. эрозия обусловливает удаление загрязнений, жёстко связанных с поверхностью (окалина, окислы и др.). Для удаления т. н. мягких загрязнений - жировых плёнок и др.- в основном используются микропотоки, возникающие вблизи пульсирующего пузырька. Воздействием на вещество в зоне кавитации пользуются для получения мелкодисперсных эмульсий, ускорения хим. реакций, экстрагирования ферментов из животных и растительных клеток и др. В установках УЗ-коагу-ляции аэрозолей используются эффекты взаимодействия частиц в УЗ-поле.

Эффекты параметрич. усиления УЗ в пьезополупро-водниках и др. явления взаимодействия эл--магн. и звуковых волн используются в акустоэлектронике. Получили развитие методы нелинейной спектроскопии, они оказались, в частности, весьма эффективными в задаче регистрации пузырьков в жидкости и существенно расширили возможности УЗ-диагностики. При облучении пузырька волнами двух частот, разность к-рых равна резонансной частоте пузырька, возникает отклик на разностной частоте, обусловленной нелинейностью пульсаций пузырька. Метод достаточно чувствителен и позволяет обнаружить даже одиночные пузырьки, что важно, напр., в биол. исследованиях или при наблюдении за режимом работы теплообменников в атомных реакторах.

Литература по нелинейной акустике

Знаете ли Вы, в чем фокус эксперимента Майкельсона?

Эксперимент А. Майкельсона, Майкельсона - Морли - действительно является цирковым фокусом, загипнотизировавшим физиков на 120 лет.

Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.

В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.

Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.