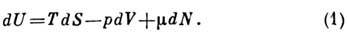
Потенциалы термодинамические - функции определённого набора термодинамич. параметров, позволяющие найти все термодинамич.
характеристики системы как функции этих параметров. Все П. т. связаны между
собой: по любому из них с помощью дифференцирования по его параметрам можно
найти все остальные потенциалы.
Метод П. т. разработан Дж. У. Гиббсом (J. W.
Gibbs) в 1874 и является основой всей термодинамики, включая теорию многокомпонентных,
многофазных и гетерогенных систем, а также термодинамич. теорию фазовых переходов. Существование П. т.- следствие 1-го и 2-го начал термодинамики. Статистич.
физика позволяет вычислять П. т. исходя из представления о строении вещества
как системы из большого числа взаимодействующих частиц.
Внутренняя энергия U(S, V, N)является П. т. в том случае, когда состояние системы характеризуется энтропией
S, объёмом V и числом частиц N, что характерно для однокомпонентных
изотропных жидкостей и газов. U наз. также изохорно-адиабатич. потенциалом.
Полный дифференциал U равен:
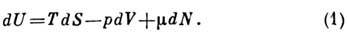
Здесь независимыми переменными являются три экстенсивные
(пропорциональные V)величины 5, V, N, а зависимыми - сопряжённые
им интенсивные (конечные в термодинамич.
пределе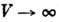 
)
величины - температура Т, давление r и химический потенциал
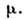Из
условия, что U есть полный дифференциал, следует, что зависимые переменные
Т, р,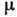
должны
быть частными производными от U:
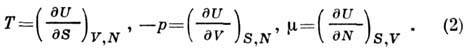
Вторая производная U по объёму даёт адиабатный
коэф. упругости:
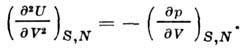
Теплоёмкость при пост. объёме равна
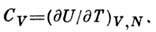
Однако это не единственно возможный выбор независимых
переменных, определяющих П. т. Их можно выбрать четырьмя разл. способами, когда
независимыми являются одна термическая и две механич. величины: S, V, N;
S, p, N; Т, V, N; Т, р, N. Для того чтобы в полном дифференциале типа (1)
заменить одну из независимых переменных ей сопряжённой, надо совершить Лежандра
преобразование, т. е. вычесть произведение двух сопряжённых переменных.
Т. о. может быть получена энтальпия H(S, p,
N)(тепловая функция Гиббса, теплосодержание, изохорно - изотермиче-ский
потенциал при независимых переменных S, p, N):
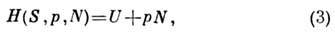
откуда следует, что
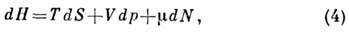
где
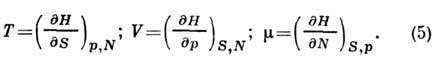
Знание H позволяет найти теплоёмкость
при пост. давлении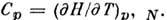
Свободная энергия F(T,V,N)(энергия
Гельмгольца, теплосодержание, изобарно-изотермич. потенциал в переменных Т,
V, N)может быть получена с помощью преобразования Лежандра от переменных
S, V, N к Т, V, N:
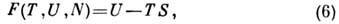
откуда
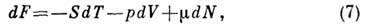
где
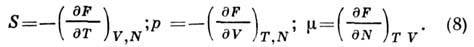
Вторые производные F по V p Г дают
теплоёмкость при пост. объёме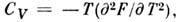
изотермич. коэф. давления
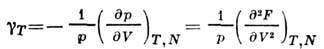
и изохорный коэф. давления
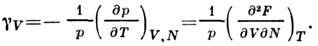
Последнее соотношение основано на независимости
второй смешанной производной от П. т. от порядка дифференцирования. Этим же
методом можно найти разность между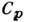 
и
:
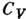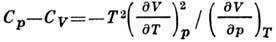
и соотношение между адиабатич. и изотермич. коэф.
сжатия:
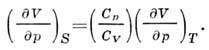
Энергия Гиббса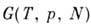 
(изобарно - изотермический потенциал в переменных Т, p, N)связана
преобразованием Лежандра с П. т. U, Н, F:
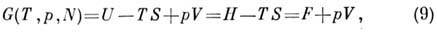
откуда
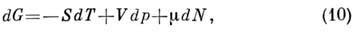
где
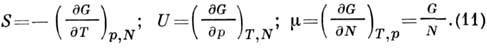
Пропорциональность G числу частиц делает
его очень удобным для приложений, особенно в теории фазовых переходов. Вторые
производные G дают теплоёмкость при пост. давлении
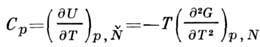
и изотермич. коэф. сжатия
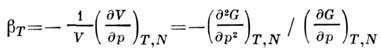
Из ур-ний (3), (5), (6), (8) следует, что П.
т. U, H, F, G связаны уравнениями Гиббса - Гельмгольца:
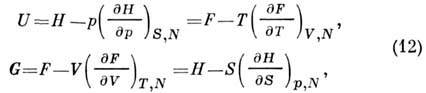
к-рые применяются для построения разд. П. т.
по экс-перим. данным о термич. и калорич. ур-ниях состояния. Необходимые для
этого граничные условия даёт предельный переход к идеальному газу и Нернста
теорема, к-рая устанавливает, что S = 0 в пределе Т
О,
и поэтому U = F и G - Н.
Для незамкнутых систем, для к-рых N не
фиксировано, удобно выбрать П. т. в переменных Т, V,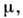
к-рый не получил специального названия и обычно обозначается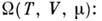
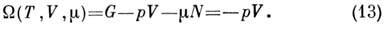
Его полный дифференциал
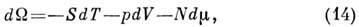
где
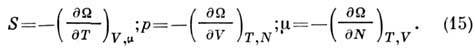
Все П. т. связаны с различными Гиббса распределениями. П. т.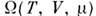
связан
с большим канонич. распределением Гиббса соотношением
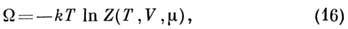
где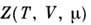 
-
статистический интеграл по фазовым
переменным и сумма по N в случае классич. механики или статистическая
сумма по квантовым состояниям. П. т. F(T, V, N)связан с канонич.
ансамблем Гиббса:
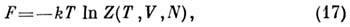
где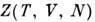 
- статистич. интеграл в классич. случае
и статистич. сумма в квантовом. П. т. Н связан с изобарно-изотермич.
ансамблем Гиббса, к-рый был предложен С. А. Богуславским (1922). П. т. /7
связан с микроканонич. распределением Гиббса через энтропию:
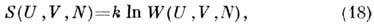
где W(U, V, N)- статистич. вес,
к-рый является нормировочным множителем для микроканонич. распределения Гиббса.
Полный дифференциал энтропии равен
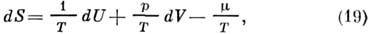
что эквивалентно ур-нию (1).
Статистич. интегралы или статистич. суммы в принципе
можно вычислить исходя из функции Гамильтона в классич. случае или оператора Гамильтона
в квантовом случае для системы из большого числа взаимодействующих частиц и
т. о. вычислить П. т. методами статистич. механики.
Кроме перечисленных П. т. применяются и другие,
напр. функции Массьё - F(T, V, N)IT, функции Планка -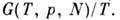
В общем случае, когда система с заданной
энтропией описывается термодинамич. параметрами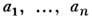
и
сопряжёнными им термодинамич. силами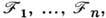
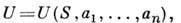
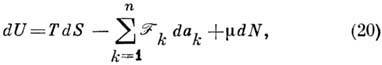
и аналогично для систем с фиксиров. энергией.
Для поляризуемых сред П. т. зависят от векторов
электрич. и магн. индукции D и В. Метод П. т. позволяет
найти тензоры электрич. и магн. проницаемостей. В изотропном случае диэлектрич.
проницаемость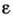
определяется из ур-ний
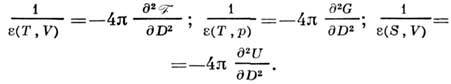
Особенно эффективно применение метода П. т. в
том случае, когда между параметрами существуют связи, напр. для изучения условий
термодинамич. равновесия гетерогенной системы, состоящей из соприкасающихся
фаз и разл. компонент. В этом случае, если можно пренебречь внеш. силами и поверхностными
явлениями, ср. энергия каждой фазы есть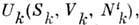
где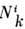
-число
частиц компоненты i в фазе k. Следовательно, для каждой из фаз
(
-
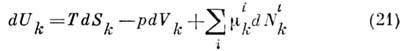
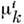хим. потенциал компоненты i в фазе k). П. т. U минимален при условии,
что полное число частиц каждой компоненты, полная энтропия и объём каждой фазы
остаются постоянными.
Метод П. т. позволяет исследовать устойчивость
термодинамич. равновесия системы относительно малых вариаций её термодинамич.
параметров. Равновесие характеризуется макс. значением энтропии или минимумом
её П. т. (внутр. энергии, энтальпии, свободной энергии, энергии Гиббса), соответствующих
независимым в условиях опыта термодинамич. переменным.
Так, при независимых S, V, N для равновесия
необходимо, чтобы была минимальна внутр. энергия, т. е.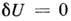 
при малых вариациях переменных и при постоянстве
S, V, N. Отсюда в качестве необходимого условия равновесия получаются
постоянство давления и температуры всех фаз и равенство хим. потенциалов сосуществующих
фаз. Однако для термодинамич. устойчивости этого недостаточно. Из условия минимальности
П. т. следует положительность второй вариации: 
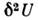> 0. Это приводит к условиям термодинамич. устойчивости, напр. к убыванию
давления с ростом объёма и положительности теплоёмкости при пост. объёме. Метод
П. т. позволяет установить для многофазных и многокомпонентных систем Гиббса
правило фаз, согласно к-рому число фаз, сосуществующих в равновесии, не
превосходит числа независимых компонентов более чем на два. Это правило следует
из того, что число независимых параметров не может превосходить числа ур-ний
для их определения при равновесии фаз.
Для построения термодинамич. теории, к-рая учитывала
бы и поверхностные явления, в вариациях П. т. следует учесть члены, пропорциональные
вариации поверхности соприкасающихся фаз. Эти члены пропорциональны поверхностному
натяжению s, к-рое имеет смысл вариац. производной любого из П. т.
по поверхности.
Метод П. т. применим также и к непрерывным пространственно неоднородным средам. В этом случае П. т. являются функционалами от плотностей термодинамич. переменных, а термодинамич. равенства принимают вид ур-ний в функциональных производных.
Д. Н. Зубарев
|
|
 |
