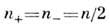
Стонера критерий ферромагнетизма - условие возникновения ферромагн.
состояния в модели коллективизиров. носителей магн. момента (см. Зонный
магнетизм). В парамагн. состоянии число п+ электронов
(на один атом) со спином, направленным вдоль направления намагниченности,
совпадает с числом п- электронов со спином, направленным
против намагниченности:
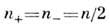
(п - общее число электронов, приходящихся на один атом). В рамках
Стонера
модели при температуре Т = 0 энергетич. подзоны электронов с противоположно
направленными спинами в результате обменного взаимодействия раздвигаются
на величину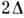 ,
пропорциональную намагниченности, что приводит к увеличению числа электронов
в подзоне с направлением спина против намагниченности [см. рис. (б,
в,)в ст. Стонера модель; при Т = 0 хим. потенциал
,
пропорциональную намагниченности, что приводит к увеличению числа электронов
в подзоне с направлением спина против намагниченности [см. рис. (б,
в,)в ст. Стонера модель; при Т = 0 хим. потенциал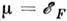 , где
, где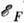 -
ферми-энергия] .При этом произойдёт изменение кинетич. энергии (в расчёте на один атом)
на величину
-
ферми-энергия] .При этом произойдёт изменение кинетич. энергии (в расчёте на один атом)
на величину
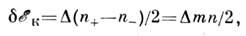
где т - относит. намагниченность,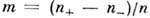 Предполагается, что величина
Предполагается, что величина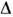 мала и можно ограничиться линейными по
мала и можно ограничиться линейными по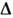 членами. Изменение магн. энергии (в расчёте на один атом) при переходе
из парамагн. состояния в ферромагнитное равно:
членами. Изменение магн. энергии (в расчёте на один атом) при переходе
из парамагн. состояния в ферромагнитное равно:
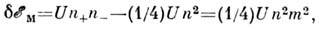
где U - параметр обменного взаимодействия. В первом порядке по
параметру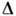 выполняется равенство
выполняется равенство
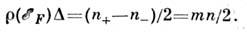
Здесь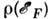 - значение плотности электронных состояний при энергии
- значение плотности электронных состояний при энергии .
Полное изменение энергии равно:
.
Полное изменение энергии равно:
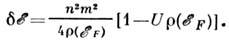
Если выполняется неравенство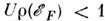 , то состоянию с наим. энергией будет соответствовать т = 0 и система
окажется в парамагн. состоянии. В противном случае,
, то состоянию с наим. энергией будет соответствовать т = 0 и система
окажется в парамагн. состоянии. В противном случае,

минимуму энергии будет соответствовать ферромагн. состояние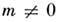 . Это условие наз. С. к. ф.
. Это условие наз. С. к. ф.
При наличии внеш. магн. поля полное изменение энергии, учитывающее зеемановское
слагаемое, имеет вид:
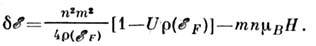
Равновесное состояние системы соответствует условию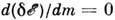 , так что магн. восприимчивость (в расчёте на атом) имеет вид:
, так что магн. восприимчивость (в расчёте на атом) имеет вид:
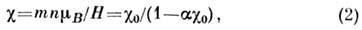
где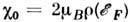 ,
,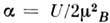 . Ф-ла
(2) описывает т. н. обменное усиление спиновой магн. восприимчивости при
. Ф-ла
(2) описывает т. н. обменное усиление спиновой магн. восприимчивости при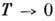 (
(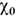 - значение
магн. восприимчивости для системы невзаимодействующих электронов,
- значение
магн. восприимчивости для системы невзаимодействующих электронов,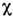 - при учёте обменного взаимодействия в среднего поля приближении или
в рамках теории ферми-жидкости; подробнее см. Паули парамагнетизм).
С помощью (2) С. к. ф. (1) может быть записан в виде
- при учёте обменного взаимодействия в среднего поля приближении или
в рамках теории ферми-жидкости; подробнее см. Паули парамагнетизм).
С помощью (2) С. к. ф. (1) может быть записан в виде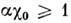 ,
выражающем условие неустойчивости парамагн. состояния
,
выражающем условие неустойчивости парамагн. состояния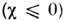 и допускающем разл. обобщения (напр., в коэф.
и допускающем разл. обобщения (напр., в коэф.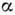 могут быть учтены не только обменные, но также корреляционные и спин-флуктуационные
эффекты).
могут быть учтены не только обменные, но также корреляционные и спин-флуктуационные
эффекты).
С. к. ф. указывает на благоприятные условия для возникновения магн.
упорядочения при больших величинах параметра обменного взаимодействия U и
при больших значениях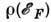 . Он показывает, почему магн. упорядочение возникает в группе 3d-металлов
(металлы с незаполненной 3d-обо дочкой). В периодич. таблице Менделеева
в ряду переходных металлов (слева направо) число электронов возрастает,
что приводит к увеличению
. Он показывает, почему магн. упорядочение возникает в группе 3d-металлов
(металлы с незаполненной 3d-обо дочкой). В периодич. таблице Менделеева
в ряду переходных металлов (слева направо) число электронов возрастает,
что приводит к увеличению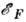 ,
а также к росту
,
а также к росту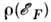 .
С др. стороны, в столбце (сверху вниз) из-за роста общего числа электронов
возрастает экранировка потенциала кулоновского взаимодействия, т. е. величина
U уменьшается. В итоге, согласно С. к. ф., в ряду Зd-металлов
вероятность ферромагнетизма зонных электронов должна уменьшаться слева
направо. Т. к. модель Стонера неинвариантна относительно вращений, С. к.
ф. оказывается завышен в пользу ферромагн. состояния из-за того, что существование
выделенной оси сильно ограничивает спектр возбуждений, а следовательно,
и энергию системы.
.
С др. стороны, в столбце (сверху вниз) из-за роста общего числа электронов
возрастает экранировка потенциала кулоновского взаимодействия, т. е. величина
U уменьшается. В итоге, согласно С. к. ф., в ряду Зd-металлов
вероятность ферромагнетизма зонных электронов должна уменьшаться слева
направо. Т. к. модель Стонера неинвариантна относительно вращений, С. к.
ф. оказывается завышен в пользу ферромагн. состояния из-за того, что существование
выделенной оси сильно ограничивает спектр возбуждений, а следовательно,
и энергию системы.
Дальнейшее обобщение С. к. ф. (иногда наз. также обобщённым критерием
Стонера - Хаббарда) возникает при переносе выражения (2) на случай неоднородной
статической восприимчивости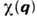 ,
q - волновой вектор. Если топология ферми-поверхности допускает
максимум
,
q - волновой вектор. Если топология ферми-поверхности допускает
максимум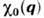 при
при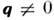 ,
то обобщённый С. к. ф.
,
то обобщённый С. к. ф.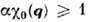 может описывать неустойчивость системы электронов относительно перехода
из однородного парамагн. состояния в неоднородное антиферромагн. (в обоих
состояниях усреднённый магн. момент равен нулю). В металлах, где поверхность
Ферми обладает свойством нестинга (имеются конгруэнтные участки при трансляции
на вектор Q, напр. в одномерном случае
может описывать неустойчивость системы электронов относительно перехода
из однородного парамагн. состояния в неоднородное антиферромагн. (в обоих
состояниях усреднённый магн. момент равен нулю). В металлах, где поверхность
Ферми обладает свойством нестинга (имеются конгруэнтные участки при трансляции
на вектор Q, напр. в одномерном случае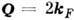 ,
где kp - ферми-импульс),
,
где kp - ферми-импульс),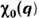 при q -> Q имеет логарифмич. особенность,
при q -> Q имеет логарифмич. особенность,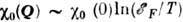 при
при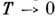 .
Тогда обобщённый С. к. ф. выполняется при сколь угодно малом значении
.
Тогда обобщённый С. к. ф. выполняется при сколь угодно малом значении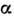 , что указывает на абсолютную неустойчивость парамагн. состояния относительно
возникновения спиновой плотности волн. Тот же эффект, описываемый
с помощью обобщённого С. к. ф. для электронной поляризуемости, проявляется
в неустойчивости системы электронов относительно возникновения волн
зарядовой плотности при учёте наряду с прямым кулоновским и обменным
также и электрон-фононного взаимодействия .
, что указывает на абсолютную неустойчивость парамагн. состояния относительно
возникновения спиновой плотности волн. Тот же эффект, описываемый
с помощью обобщённого С. к. ф. для электронной поляризуемости, проявляется
в неустойчивости системы электронов относительно возникновения волн
зарядовой плотности при учёте наряду с прямым кулоновским и обменным
также и электрон-фононного взаимодействия .

А. В. Ведяев, О. А. Котелъникова
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|