Приближение среднего поля. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Приближение среднего поля (молекулярное поле ,эффективное поле) - один из методов приближённого описания эффектов многочастичных взаимодействий в задачах многих тел в квантовой механике и квантовой статистике. С, п. п. применяется в тех случаях, когда точное решение задачи отсутствует, а учёт конечного числа членов ряда возмущений теории недостаточен (напр., если константа взаимодействия не мала или ряды теории возмущений обладают плохой сходимостью). С. п. п. состоит обычно в эфф. «линеаризации» гамильтониана взаимодействия мн, частиц, т. е. в замене его соответственно подобранным гамильтонианом одночастичного взаимодействия с нек-рым эфф. «полем», параметры к-рого следует определить самосогласованным образом. Физически такая замена соответствует переходу от «близкодействия» к «дальнодействию», т. е. к постоянному (не зависящему от расстояния) многочастичному взаимодействию с формально бесконечным радиусом, а также пренебрежению корреляц. эффектами. Несмотря на такое упрощение решения задачи мн. тел С. п. п. в большинстве случаев качественно правильно описывает физ. свойства очень широкого класса реальных систем мн. тел, в первую очередь сложных атомов, молекул, жидкостей и твёрдых тел (см. Самосогласованное поле, Хартри - Фока метод).

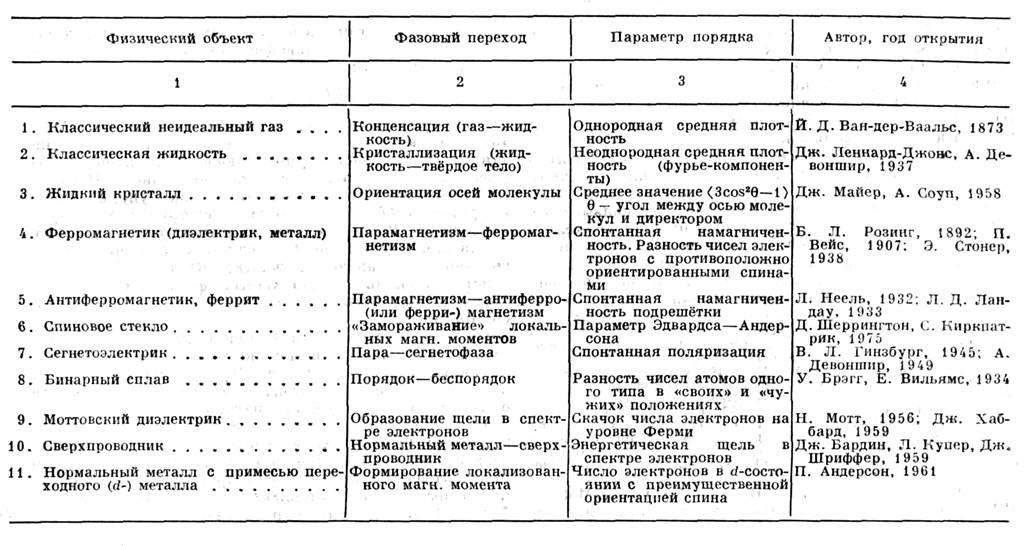
Особенно важное значение С. п. п. имеет для решения задач физики конденсиров. состояния, прежде всего для описания разл. подсистем в твёрдых телах (столбец 1 в табл.), испытывающих разнообразные фазовые переходы (структурные, ориентационные, магнитные, сверхпроводящие и т. п.- столбец 2 в табл.). В подобных системах среднее поле (СП) принимается обычно пропорциональным параметру порядка (столбец 3 в табл.), т. е. ср. значению оператора упорядочения (оператор, описывающий динамическую переменную, испытывающую упорядочение). Физически это означает пренебрежение квантовыми флуктуациями этого оператора и построенными на них высшими корреляционными функциями. При этом СП оказывается зависящим от внеш. полей, температуры и др. интенсивных термодинамич. параметров (для структурно неупорядоченных систем СП может быть неоднородным, т. е. зависеть от координат). С. п. п. позволяет вычислить статистическую сумму и все термодинамич. функции системы. Дальнейшая процедура самосогласования приводит обычно к достаточно простому ур-нию (в большинстве случаев - трансцендентному, иногда, как в случае сверхпроводника,- интегральному) для параметра порядка. Это ур-ние имеет нетривиальные (отличные от нуля) решения лишь ниже определ. температуры Т_к, называемой критической точкой или точкой фазового перехода 1-го или 2-го рода. При этом значение энергии взаимодействия системы со СП в осн. состоянии при Т = 0 составляет величину порядка kT_k.

Физ. смысл СП столь же разнообразен, сколь разнообразны виды систем и параметров порядка; как правило, СП определяется произведением параметра порядка на ср. энергию взаимодействия частиц системы. Так, в магнитоупорядоченных веществах (в т. ч. спиновых стёклах)и сегнетоэлектриках это - обменное взаимодействие, в сверхпроводниках - электрон-фо-нонное взаимодействие, в переходах металл - диэлектрик - внутриатомное кулоновское отталкивание между электронами, в классич. газах и жидкостях - межмолекулярное притяжение и т. п. До возникновения микроскопич. описания С. п. п. вводилось чисто феноменологически и лишь затем получало обоснование и истолкование через микроскопич. параметры; как видно из столбца 4 таблицы, С. п. п. фактически применяется уже более ста лет, т. е. задолго до возникновения квантовой теории.

Исторически первое целенаправленное введение СП (тогда - внутреннего, или молекулярного, поля) считается принадлежащим Б. Л. Розингу (1892) и П. Вейсу (P. Weiss, 1907), применившим его в теории ферромагнетизма для объяснения существования спонтанной намагниченности. Однако ещё задолго до этого И. Д. Ван-дер-Ваальс (J. D. Van der Waals, 1873) фактически использовал понятие СП для учёта межмолекулярного взаимодействия при выводе ур-ния состояния классич. неидеального газа.

В дальнейшем (30-е гг. 20 в.) С. п. п. плодотворно применялось рядом авторов к широкому классу объектов (антиферромагнетики, ферриты, бинарные сплавы и т. п.), а позднее (40-50-е гг.) - к сегнетоэлектрикам, сверхпроводникам и др. С. п. п. успешно используется также в теории неупорядоченных систем (аморфные твёрдые тела, спиновые стёкла и т. п.). Практически все эти системы могут быть описаны с помощью эффективного спинового гамильтониана. При этом оператором упорядочения является одна из компонент S^a оператора спина (квазиспина) S. В магнитоупорядоченных веществах таким оператором будет продольная (Изинга модель)или поперечная (ХУ-модель; см. Двумерные решёточные модели)компонента оператора спина. В сверхпроводниках оператором упорядочения является поперечная компонента оператора квазиспина (совпадающая с оператором рождения куперовской пары), в ферромагн. металле - продольная компонента оператора квазиспина (разность операторов числа электронов с противоположными спинами). Процедура введения СП состоит в замене одного из операторов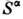

его ср. значением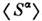

, что позволяет линеаризовать гамильтониан и получить точное решение в рамках данной модели.

С. п. п. фактически эквивалентно применению вариационного принципа Н. Н. Боголюбова для свободной энергии (напр., применительно к магн. диэлектрикам) а также разложения свободной энергии по степеням параметра порядка вблизи критич. точки и гауссовому приближению в методе континуального интегрирования для статистич. суммы. Ввиду своей физ. наглядности и матем. простоты С. п. п. является, как правило, необходимым первоначальным этапом решения задачи мн. тел практически для любой системы, особенно при наличии в ней дополнит. усложнений - сложной структуры кристаллич. или магн. элементарной ячейки, нарушения регулярной структуры кристалла, т. е. наличия примесей, вакансий и др. дефектов (см., напр., Магнитный фазовый переход ).Однако в рамках С. п. п. невозможно описать динамич. свойства систем, прежде всего спектр элементарных возбуждений, резонансные свойства и т. п.

Применимость С. п. п. имеет определ. ограничения. Прежде всего оно теряет пригодность в тех случаях, когда флуктуации параметра порядка играют существ. роль, напр. в непосредств. окрестности точек фазовых переходов, где С. п. п. даёт завышенные значения самих этих точек, а также не согласующиеся с экспериментом значения критических показателей. С. п. п. не «чувствует» тонких различий между нек-рыми системами (напр., ферромагнетиками Изинга и Гейзенберга) и даёт значения критич. показателей, не зависящие ни от размерности решётки d, ни от размерности параметра порядка п. К системам с низкой размерностью (d - 1,2), для к-рых имеющиеся точные решения модельных задач или общие теоремы квантовой статистич. механики указывают на отсутствие фазовых переходов, С. п. п. вообще неприменимо.

Одним из обобщений С. п. п. (используемых, в частности, для магн. и сегнетоэлектрич. систем) является разложение свободной энергии и корреляц. функций по обратным степеням радиуса обменного воздействия. Широко применяется также метод ренормализационной группы и e-разложения, приводящий к появлению «траекторий» на плоскости (п, d)для критич. показателей, значения к-рых близки к экспериментально наблюдаемым.

Другим важнейшим обобщением С. п. п. является т. н. приближение случайных фаз (ПСФ), к-рое представляет собой развитие идеи усреднения соответствующих операторов упорядочения. При этом усреднение операторов осуществляется не в гамильтониане, а при записи квантового уравнения движения. наиб. завершение эта идея получила в методе функций Грина. В квантовой теории магнетизма ПСФ носит название приближения Тябликова, в теории сверхпроводимости - Бардина - Купера - Шриффера модели, в теории неупорядоченных систем - приближения когерентного потенциала. ПСФ соответствует учёту влияния на каждое одночастичное состояние не только ср. статич. поля, как в С. п. п., но и переменных (осциллирующих) добавок к нему, возникающих благодаря частичному учёту корреляции между движениями различных (квази) частиц.

С. п. п. соответствует учёту только дальнего порядка, однако существует ряд способов его улучшения с целью учёта также эффектов корреляции, проявляющихся в наличии ближнего порядка. Среди них наиб. известны т. н. кластерные приближе-н и я. При этом оператор упорядочения задаётся не для узла решётки, а для кластера, включающего, напр., первую координац. сферу.

Литература по приближению среднего поля

Знаете ли Вы, что такое "усталость света"?
Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.