Сферическая волна. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Сферическая волна - волна, радиально расходящаяся от нек-рой точки (источника) или сходящаяся к ней (к стоку) и имеющая сферич. волновые фронты (поверхности равных фаз). Простейшим примером является сферически симметричная скалярная волна вида

расходящаяся от центр. точки r = 0 (знак " -") или сходящаяся к ней (знак "+") со скоростью с. Такая волна удовлетворяет волновому уравнению и описывает многие физ. процессы в линейных средах без дисперсии и без потерь. Суперпозиция сходящейся и расходящейся волн (в частности, стоячая С. в.) также является решением волнового ур-ния.

функция f в общем случае произвольна; важный частный случай - гармоническая С. в.: f=A expi(wt + kr); в такой волне А/r - амплитуда, а wt + kr = Ф - фаза (w - круговая частота, k - волновое число).

Если величина u(r, t)описывает физ. поле (напр., возмущение давления в звуковой волне, скалярный потенциал в эл--магн. волне и др.), то плотность потока энергии поля, уносимой от источника или приносимой к нему, пропорц. |u(r, t)|², и, следовательно, общий поток энергии через сферу любого радиуса r, пропорц. 4pr²|и|², сохраняется неизменным. Это является следствием закона сохранения энергии.

При наличии поглощения в среде энергия С. в. убывает в направлении её распространения. Для гармонии. С. в. поглощение может быть учтено заменой k на k' + k'', где k'' - мнимая часть волнового числа. Это означает, что амплитуда волны затухает по экспоненте:

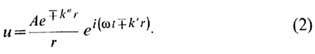
Существуют и несимметричные С. в., амплитуды к-рых зависят от полярной q и азимутальной j угл. координат, но фазовые фронты по-прежнему остаются сферическими:

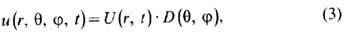
где U(r, t)отвечает симметричной С. в., напр. в форме (1) или (2), a D(q, j) описывает угл. зависимость поля (эту функцию можно представить в виде суперпозиции т. н. сферич. гармоник). В однородных изотропных средах волновое поле на больших расстояниях от центра почти всегда имеет вид (3). Подбором D можно концентрировать поле около заданных направлений, поэтому функция D(q, j) наз. диаграммой направленности излучения источника (см. Антенна).

Литература по сферическим волнам

Знаете ли Вы, что электромагнитное и другие поля есть различные типы колебаний, деформаций и вариаций давления в эфире.

Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.

В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.