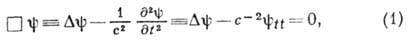
Волновое уравнение. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Волновое уравнение - линейное однородное ур-ние в частных производных гиперболич. типа:

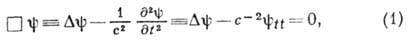
где t - время, с - пост. параметр, имеющий размерность скорости,

- Д-Аламбера оператор ,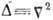

- Лапласа оператор. Иногда вместо в (1) используют оператор Лоренца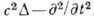

. Векторное волновое уравнение предусматривает применение оператора

к каждой из декартовых компонент вектора; при переходе к произвольным координатам используют тождество

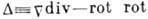Первоначально волновое уравнение получено в одномерном варианте применительно к описанию движения упругой струны практически одновременно Д. Бернулли (D. Bernoulli), Ж. Д-Аламбером (J. d'Alembert) и Л. Эйлером (L. Euler) в 40-е гг. 18 века Бернулли выразил его решение через тригонометрич. ряды, Д-Аламбер и Эйлер записали общее решение в виде двух перемещающихся в пространстве со скоростью с возмущений (волн):

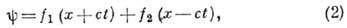
что и дало основание назвать ур-ние (1) волновым. Эквивалентность тригонометрич. представления решения волнового уравнения функциональной записи (2) доказана Ж. Фурье (J. Fourier) в 1824.

Впоследствии понятие волнового возмущения претерпело значит. изменения (см. Волны), поэтому (1) нельзя считать универсальным и единственным волновым уравнением; оно охватывает отнюдь не все виды движений, квалифицируемых сейчас как волновые. Иногда, напр., термин "уравнение волны" применяется к упрощённому уравнению 1-го порядка

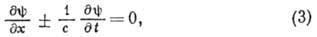
описывающему волну (моду), распространяющуюся только в одном направлении. Ур-ние (3) можно интерпретировать как закон сохранения величины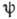

, поэтому его иногда наз. "кинематическим", в отличие от "динамического" ур-ния 2-го порядка или от системы двух ур-ний 1-го порядка (см., напр., Телеграфные уравнения).

Ур-ния (1) и (3) порождают достаточно разветвлённое семейство ур-ний, также причисляемых по совр. терминологии к категории волновых. Простейшим обобщением, сохраняющим внеш. облик ур-ния (1), является введение в него зависимости скорости с от координат, с=с(r)(неоднородные среды), от времени (параметрические среды), от самой функции

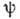(квазилинейные среды) или от частоты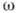

её изменения во времени,

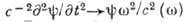(диспергирующие среды).

Волновое уравнение является одной из наиб. употребит. матем. моделей в физике. Оно описывает почти все разновидности малых колебании в распределённых механич. системах (продольные звуковые колебания в газе, жидкости, твёрдом теле; поперечные колебания в струнах и т. п.). Ему удовлетворяют компоненты эл--магн. векторов и потенциалов, и, следовательно, мн. эл--магн. явления (от квазистатики до оптики) в той или иной мере объясняются свойствами его решений.

Инвариантные преобразования

Ур-ние (1) инвариантно (т. е. сохраняет свою структуру) относительно линейных преобразований координат и времени, объединённых в 10-параметрическую Пуанкаре группу (3 вращения вокруг пространственных осей, 3 равномерных движения вдоль них, объединяемые в Лоренца преобразования ,а также 4 смещения начала координат и времени). В 1910 Г. Бейтмен (H. Bateman) показал, что волновое уравнение инвариантно относительно 15-параметрич. конформной группы, содержащей в качестве подгруппы группу Пуанкаре. Из др. инвариантных преобразований следует выделить:

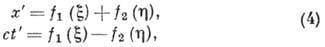
где f₁ и f₂ - произвольные функции своих аргументов: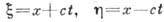

. Прямые

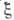=const,

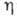=const наз. характеристиками; в этих координатах одномерное волновое уравнение (1) факторизуется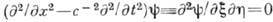

Следовательно, преобразование (4) означает, что любая функция характеристики сама является характеристикой. Разделение переменных. Ур-ние (1) всегда допускает разделение переменных, т. е. факторизацию решения по координатам и времени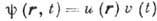

, при этом

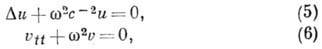
т. е. для функции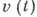

получается ур-ние осциллятора (6), а для и(r) - трёхмерное Гелъмголъца уравнение, в двумерном случае его называют также ур-нием мембраны, а в одномерном - ур-нием осциллятора (но уже пространственного, а не временного).

В декартовых координатах волновое уравнение (1) можно свести к набору четырех ур-ний осцилляторов: трёх пространственных

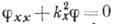и одного временного (6). Постоянные разделения k_x, k_y, k_z можно интерпретировать как компоненты нек-рого вектора k, наз. волновым вектором, поскольку плоская волна вида

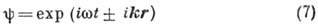
является собств. решением (1) при условии: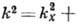

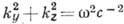. Комплексная запись (7) включает в себя сразу два решения, соответствующие действительной и мнимой частям. Помимо декартовой системы координат, переменные в ур-нии Гельмгольца (5) разделяются в цилиндрических (полярной, эллиптич. и параболич.), сферической и сфероидальных (вытянутой и сплюснутой) системах.

Неоднородное волновое ур-ние содержит в правой части функцию источника

и наз. Д-Аламбера ур-нием. Его решение состоит из собств. мод - решений однородного ур-ния (1) и из вынужденного решения, связанного с источником. В силу линейности (8) справедлив суперпозиции принцип, поэтому функцию f можно разложить по любой полной системе функций (обычно выраженных через координаты, допускающие разделение переменных) или представить в виде интеграла (суммы) по элементарным источникам. Часто в качестве элементарного источника берётся дельта-функция Дирака, а соответствующее решение наз. Грина функцией. Всплеск от элементарного возмущения, имевшего место в начале координат в момент t=0, возбуждает волны, уходящие (бегущие, распространяющиеся) от источника. В одномерном случае их величина постоянна, в двумерном и трёхмерном - она монотонно убывает с удалением от центра. Для двумерного пространства характерно возникновение бесконечно длящегося последействия, благодаря к-рому отклик не повторяет функцию источника.

Обычно для волнового уравнения рассматривают Коши задачу, описывающую распространение волн в n-мерном пространстве. Классич. решением задачи Коши наз. непрерывно дифференцируемую функцию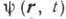

, удовлетворяющую волновому уравнению в полупространстве t > 0 и нач. условиям

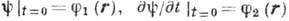, где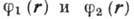

- заданные функции. Классич. решение даётся Кирхгофа формулой (п = 3), Пуассона формулой (n=2) или Д-Аламбера формулой (n=1). Рассматривают также смешанную задачу, описывающую колебания ограниченного объёма V.

Имеется много приближённых методов решения волнового уравнения. В т. н. KB-асимптотике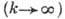

рассматривают параболического уравнения приближение ,к-рое позволяет анализировать свойства волновых пучков и волновых пакетов, т. е. волновых образований, локализованных в пространстве и во времени, и геометрической оптики метод.

В системах с дисперсией волн возникает искажение профиля волны, обусловленное зависимостью скорости распространения её разл. участков от их крутизны, и решение в виде (2) становится невозможным. Если такую волну представить в виде суперпозиции синусоидальных мод типа (7), то дисперсия проявляется как зависимость фазовых скоростей с этих мод от частоты. Тогда соотношение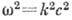

следует рассматривать как дисперсионное уравнение, заменяющее исходное волновое уравнение (1) и в нек-ром смысле обладающее даже большей общностью, поскольку учёт зависимости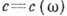

можно провести только в рамках ур-ния Гельмгольца, т. е. после введения синусоидальной зависимости от времени. По виду дисперсионного ур-ния (в частности, если оно представляется полиномами конечных степеней по w и k) можно восстановить вид исходного дифференц. ур-ния, описывающего данный класс волн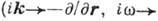

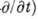; эти ур-ния могут существенно отличаться от стандартного ур-ния (1). Наиб. важной и наглядной иллюстрацией являются волны на поверхности жидкости .Напр., длинным (по сравнению с глубиной бассейна) волнам при небольших амплитудах соответствует дисперсионное ур-ние вида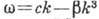

, по к-рому легко восстанавливается исходное дифференц. ур-ние

. Это т. н. линеаризованное Кортевега-де Фриса уравнение, один из возможных вариантов обобщения ур-ния (3) на системы с дисперсией.

Нелинейные волновые уравнения

При перечислении нелинейных обобщений В. у. необходимо проявлять нек-рую сдержанность, с тем чтобы при этом не утрачивалась связь с исходным В. у. В этом смысле единственным терминологически точным обобщением является внесение зависимости скорости с от волновой функции в ур-ния (1), (3) или (8). Однако часто к нелинейным В. у. относят любые ур-ния, вырождающиеся в линейные В. у. при устранении нелинейности или линеаризации. Наиб. известны нелинейное ур-ние Клейна-Гордона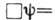

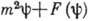, обобщающее линейное Клейна-Гордона уравнение, и нелинейное ур-ние Гельмгольца

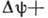
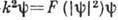, учитывающее зависимость волнового числа от квадрата волновой функции.

Нелинейные В. у. позволяют описать взаимодействие волн (в т. ч. и квазимонохроматических), возникновение и эволюцию ударных волн и солитонов, самофокусировку и самоканализацию и т. д.

Литература по волновым уравнениям

Знаете ли Вы, что, когда некоторые исследователи, пытающиеся примирить релятивизм и эфирную физику, говорят, например, о том, что космос состоит на 70% из "физического вакуума", а на 30% - из вещества и поля, то они впадают в фундаментальное логическое противоречие. Это противоречие заключается в следующем.

Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.