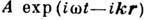 . Циклич. частоты
. Циклич. частоты 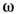 и волновые векторы k нормальных волн связаны дисперсионным уравнением
и волновые векторы k нормальных волн связаны дисперсионным уравнениемДисперсия волн - в линейных системах зависимость фазовой скорости гармонич. волн от частоты (длины
волны) и, как следствие, изменение формы произвольных (негармонич.) волновых
возмущений в процессе их распространения. Термин "дисперсия" (от
лат. dispergo - рассеивать, развеивать, разгонять) был введён в физику И. Ньютоном
(I. Newton) в 1672 при описании разложения пучка белого света, преломляющегося
на границе раздела сред. Волновая концепция позволила объяснить это явление
зависимостью скорости распространения монохроматич. волн от частоты (цвета).
В результате под Д. в. стали понимать именно эту зависимость, относя к следствиям
Д. в. такие физ. эффекты, как расплывание импульсов, различие фазовой и групповой
скоростей, неравномерное движение волновых фронтов и т. д. Иногда термин "Д.
в." используется для обозначения разложения волнового поля в гармонич.
спектр (напр., при прохождении волны через дифракц. решётку). Последующая эволюция
понятия Д. в. связана с его обобщениями на поглощающие, активные, параметрические
и нелинейные системы (среды, волноводы, поверхности жидкостей и т. д.).
Традиц. описание Д. в.
основано на представлении произвольного волнового поля в линейных однородных
системах в виде совокупности гармонич. нормальных волн 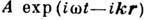 . Циклич. частоты
. Циклич. частоты 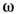 и волновые векторы k нормальных волн связаны дисперсионным уравнением
и волновые векторы k нормальных волн связаны дисперсионным уравнением

в изотропных средах 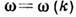 ,
, 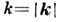 - волновое
число. Д. в. имеет место, если соотношение (1) не сводится к линейному и однородному.
Ключевыми понятиями при анализе процесса Д. в. являются фазовые
- волновое
число. Д. в. имеет место, если соотношение (1) не сводится к линейному и однородному.
Ключевыми понятиями при анализе процесса Д. в. являются фазовые 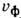 и групповые vгр скорости. Они различаются между собой (в анизотропных
средах не только по величине, но и по направлению); совпадают лишь при отсутствии
Д. в., когда
и групповые vгр скорости. Они различаются между собой (в анизотропных
средах не только по величине, но и по направлению); совпадают лишь при отсутствии
Д. в., когда 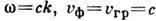 .
Существует нек-рый разнобой в терминологии, характеризующей Д. в. Так, в классич.
оптике Д. в. считается нормальной (или отрицательной), если фазовая скорость
уменьшается с ростом частоты, и аномальной (или положительной), если
.
Существует нек-рый разнобой в терминологии, характеризующей Д. в. Так, в классич.
оптике Д. в. считается нормальной (или отрицательной), если фазовая скорость
уменьшается с ростом частоты, и аномальной (или положительной), если 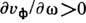 . Однако в квантовой оптике понятие отрицательной Д. в. относят к случаю распространения
света в неравновесных средах с отрицательной силой осцилляторов; а в электронике
Д. в. наз. аномальной, если фазовая и групповая скорости направлены в противоположные
стороны (обратные волны).
. Однако в квантовой оптике понятие отрицательной Д. в. относят к случаю распространения
света в неравновесных средах с отрицательной силой осцилляторов; а в электронике
Д. в. наз. аномальной, если фазовая и групповая скорости направлены в противоположные
стороны (обратные волны).
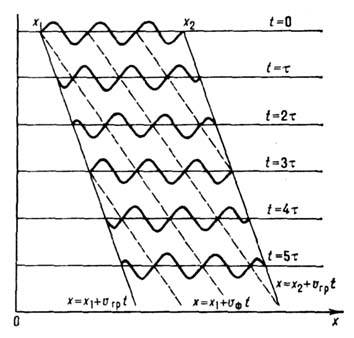
Рис. 1. Цуг на глубокой
воде Наблюдатель 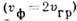 в
каждый момент времени видит три гребня; однако, измеряя их число неподвижным
датчиком, он зарегистрирует шесть всплесков.
в
каждый момент времени видит три гребня; однако, измеряя их число неподвижным
датчиком, он зарегистрирует шесть всплесков.
Строго говоря, 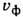 и
и 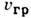 определяются
для квазигармонич. волновых пакетов (длинных цугов волн), групповая скорость
примерно совпадает со скоростью движения огибающей цуга, а фазовая-со скоростью
перемещения вариаций поля (рис. 1). Искажениями огибающей цуга и его фазовой
структуры можно пренебречь только на ограниченных участках трассы распространения
длиной
определяются
для квазигармонич. волновых пакетов (длинных цугов волн), групповая скорость
примерно совпадает со скоростью движения огибающей цуга, а фазовая-со скоростью
перемещения вариаций поля (рис. 1). Искажениями огибающей цуга и его фазовой
структуры можно пренебречь только на ограниченных участках трассы распространения
длиной 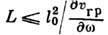 , где
l0-исходная длина волнового пакета. На длинных трассах
, где
l0-исходная длина волнового пакета. На длинных трассах 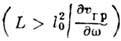 цуг расплывается, его характерный размер растёт пропорционально пройденному
пути:
цуг расплывается, его характерный размер растёт пропорционально пройденному
пути: 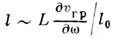 (рис. 2).
В непоглощающих (и слабопоглощающих) средах vгр совпадает
со скоростью переноса
энергии, а следовательно, и со скоростью передачи информации, закодированной
с помощью амплитудной или фазовой модуляции.
(рис. 2).
В непоглощающих (и слабопоглощающих) средах vгр совпадает
со скоростью переноса
энергии, а следовательно, и со скоростью передачи информации, закодированной
с помощью амплитудной или фазовой модуляции.
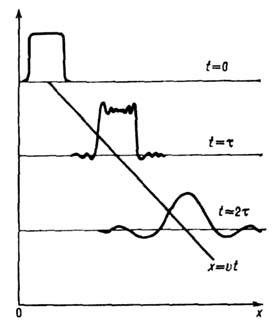
Рис. 2. Пример расплывания волнового пакета. Сначала огибающая импульса искажается в окрестностях наиболее крутых участков (фронтов). При больших временах импульс, продолжая передвигаться в среднем с групповой скоростью, расширяется, а форма его огибающей приближённо повторяет форму пространственного спектра исходного сигнала.
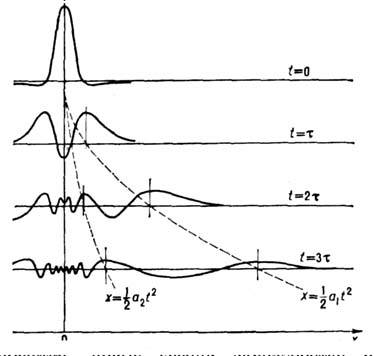
Рис. 3. Схема разбегания волн на глубокой воде от одиночного всплеска.
В случае произвольных волновых
возмущений, не близких к гармоническим, Д. в. может приводить к сложным явлениям.
Напр. при разбегании поверхностных волн на глубокой воде от одиночного одномерного
всплеска (рис. 3) число волновых гребней постоянно увеличивается; новые гребни
зарождаются парами, один из них равноускоренно удаляется от места всплеска,
постепенно расплываясь, другой, становясь круче, асимптотически приближается
к оси симметрии всплеска.
Ускорение первого гребня гравитац. волны а1=0,325g, второго
а2=0,069g, где g - ускорение свободного падения.
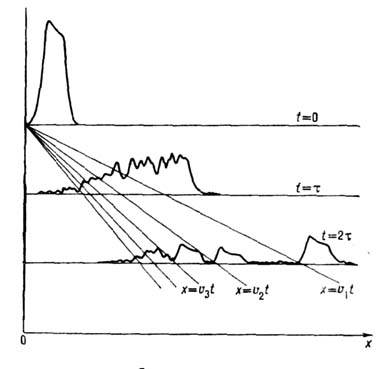
Рис. 4. Распространение квазимонохроматического сигнала в многомодовом волноводе.
При неоднозначной зависимости
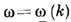 выделяют отд.
ветви нормальных волн - моды .В однородных средах они различаются либо
поляризацией (напр.,
обыкновенные и необыкновенные
волны в анизотропных кристаллах или в замагниченной плазме), либо природой формирующих
волну взаимодействий (напр., ленгмюровские и ионно-звуковые волны в плазме). В волноводных системах, кроме того, моды различаются поперечной структурой
полей. Каждой моде могут быть сопоставлены фазовые и групповые скорости. Одиночный
импульсный сигнал, запущенный в многомодовую систему, распадается на серию отд.
сигналов, распространяющихся с разл. групповыми скоростями (рис. 4).
выделяют отд.
ветви нормальных волн - моды .В однородных средах они различаются либо
поляризацией (напр.,
обыкновенные и необыкновенные
волны в анизотропных кристаллах или в замагниченной плазме), либо природой формирующих
волну взаимодействий (напр., ленгмюровские и ионно-звуковые волны в плазме). В волноводных системах, кроме того, моды различаются поперечной структурой
полей. Каждой моде могут быть сопоставлены фазовые и групповые скорости. Одиночный
импульсный сигнал, запущенный в многомодовую систему, распадается на серию отд.
сигналов, распространяющихся с разл. групповыми скоростями (рис. 4).
Д. в. объясняется инерционностью
и нелокальностью формирующих волну взаимодействий. Практически во всех реальных
системах отклик на кратковременное сосредоточенное воздействие растянут во времени
и размыт в пространстве. Соответствующие характерные времена инерционности 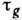 и масштабы нелокальности
и масштабы нелокальности 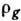 определяются либо микропроцессами в диспергирующей среде, либо переотражениями
на макроскопич. неоднородностях и границах волноводной системы. В ряде случаев
эффекты инерционности и нелокальности проявляются независимо; при этом различают
временную и пространственную дисперсию соответственно. Однако в нек-рых системах
инерционность и нелокальность неразрывно взаимосвязаны, и тогда характер Д.
в. определяется др. физ. величинами, имеющими, следовательно, более сложную
размерность. Напр., для гравитационных поверхностных волн на глубокой воде параметром
дисперсии является ускорение свободного падения
определяются либо микропроцессами в диспергирующей среде, либо переотражениями
на макроскопич. неоднородностях и границах волноводной системы. В ряде случаев
эффекты инерционности и нелокальности проявляются независимо; при этом различают
временную и пространственную дисперсию соответственно. Однако в нек-рых системах
инерционность и нелокальность неразрывно взаимосвязаны, и тогда характер Д.
в. определяется др. физ. величинами, имеющими, следовательно, более сложную
размерность. Напр., для гравитационных поверхностных волн на глубокой воде параметром
дисперсии является ускорение свободного падения 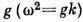 , для капиллярных волн - отношение коэф. поверхностного натяжения
, для капиллярных волн - отношение коэф. поверхностного натяжения 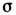 к плотности жидкости
к плотности жидкости 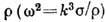 ,
для волн де Бройля - отношение постоянной Планка
,
для волн де Бройля - отношение постоянной Планка 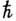 к массе частицы
к массе частицы 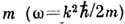 .
.
Существует обширный класс
явлений, описание к-рых не сводится к изучению свойств отд. гармонич. волн,
ибо последние просто могут не являться собств. движениями в соответствующих
системах. В этих случаях понятие Д. в. не допускает универсального определения,
хотя всякий раз оно в той или иной степени оказывается связанным с инерционностью
и нелокальностью взаимодействий.
В линейных системах с потерями
волновые возмущения также могут быть представлены как совокупность экспоненциальных
нормальных волн 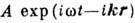 , но уже с комплексными значениями частот
, но уже с комплексными значениями частот 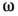 и
волновых векторов k, мнимые части к-рых определяют временные
и
волновых векторов k, мнимые части к-рых определяют временные 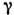 и пространственные Г декременты затухания
и пространственные Г декременты затухания 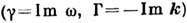 . Д. в. приводит к селективности потерь,
т. е. к их зависимости от
. Д. в. приводит к селективности потерь,
т. е. к их зависимости от 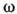 или k. Декремент
или k. Декремент 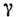 и действит. часть частоты
и действит. часть частоты 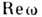 в силу причинности принципа не могут быть произвольными функциями k
- соответствующие ограничения даются дисперсионными соотношениями.
в силу причинности принципа не могут быть произвольными функциями k
- соответствующие ограничения даются дисперсионными соотношениями.
В плавно неоднородных средах
волновое поле достаточно хорошо описывается в приближении геометрической
оптики метода, т. е. его можно представить как совокупность волн вида 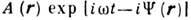 . Аналогом дисперсионного ур-ния (1) в данном случае является ур-ние эйконала
. Аналогом дисперсионного ур-ния (1) в данном случае является ур-ние эйконала 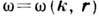 , связывающее
частоту
, связывающее
частоту 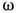 с локальным
значением волнового вектора
с локальным
значением волнового вектора 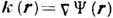 . Закон дисперсии определяет ур-ния лучей:
. Закон дисперсии определяет ур-ния лучей:

В неоднородных средах Д.
в. приводит к дополнит. эффекту - зависимости трассы распространения (лучей)
от частоты. В системах с изменяющимися во времени параметрами (параметрических
колебательных системах), кроме того, вдоль трассы распространения изменяется
частотный спектр сигнала. В средах, где характерные размеры неоднородностей
сравнимы с масштабами изменения поля, эффекты Д. в. часто нельзя отделить от
дифракционных эффектов.
В нелинейных системах суждение
о Д. в. может быть составлено на основе представлений об инерционности и нелокальности
линейных взаимодействий (соответствующие свойства нелинейных взаимодействий
иногда квалифицируют как нелокальность нелинейности). Примером, объединяющим
нелинейность и дисперсию, может служить класс физ. явлений, описываемых Кортевега
- де Фриса уравнением, впервые полученным (1895) для волн на мелкой воде:
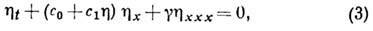
где 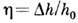 - относительное возмущение поверхности, h0 - глубина водоёма,
- относительное возмущение поверхности, h0 - глубина водоёма,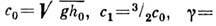
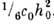 . В приближении малых амплитуд
. В приближении малых амплитуд 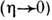 можно пренебречь нелинейностью; тогда ур-нию (3) соответствует дисперсионное
ур-ние вида
можно пренебречь нелинейностью; тогда ур-нию (3) соответствует дисперсионное
ур-ние вида
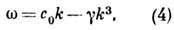
Как следует из (4), ответственным
за Д. в. является последний член в (3). В случае плавных возмущений, характерные
масштабы к-рых 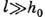 , можно пренебречь Д. в., и тогда (3) переходит в ур-ние простой волны, в к-рой
амплитуда
, можно пренебречь Д. в., и тогда (3) переходит в ур-ние простой волны, в к-рой
амплитуда 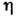 постоянна
вдоль характеристик
постоянна
вдоль характеристик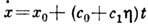
По мере распространения
такого плавного возмущения (рис. 5) передний фронт волны становится круче; в
отсутствие Д. в. это привело бы в конечном счёте к его обрушению. Однако Д.
в. останавливает этот процесс, и волна становится сначала изрезанной, а затем
разбивается на серию почти автономных, сохраняющих форму всплесков (солитонов), каждый из к-рых движется со своей скоростью. Существование стационарных
нелинейных волн (солитонов и периодич. кноидальных волн) является важным проявлением
Д. в., присущим многим нелинейным системам. При этом амплитуда, скорость и характерная
длина оказываются связанными нелинейными дисперсионными ур-ниями; соответственно,
зависимость скорости стационарной волны от её структурных параметров наз. нелинейной
Д. в. Относительно др. дисперсионных эффектов в нелинейных, в т. ч. и диссипативных,
средах см. Нелинейные колебания и волны, Бюргерса уравнение, Ударная волна.
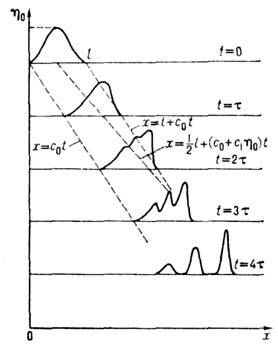
Рис. 5. Распространение
длинной волны в нелинейной системе с реактивной дисперсией.
Неодномерные волновые возмущения
даже в однородных недиспергирующих средах демонстрируют иногда поведение, имитирующее
Д. в. Наиб. известным и часто встречающимся примером являются цилиндрич. импульсные
сигналы в свободном пространстве, оставляющие за собой бесконечно тянущиеся
шлейфы. Эти эффекты также порой относят к Д. в., хотя они не удовлетворяют её
канонич. определениям.

M. А. Миллер, Г. В. Пермитин
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.
|
|