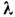 = 1,55 мкм) и устойчивости модовой структуры излучения при возрастании
входной мощности вплоть до значений, близких к порогу самофокусировки.
= 1,55 мкм) и устойчивости модовой структуры излучения при возрастании
входной мощности вплоть до значений, близких к порогу самофокусировки.
Солитоны оптические - оптические импульсы, сохраняющие структурную
устойчивость огибающей при распространении в нелинейной среде даже при
наличии возмущающих факторов и взаимодействий с др. С. В зависимости от
характера нелинейного взаимодействия излучения с веществом солитонные эффекты
в оптике разделяют на резонансные и нерезонансные. В нерезонансных средах
оптич. С. формируются в результате баланса двух конкурирующих процессов
- дисперсионного расплывания (см. Дисперсия света)и нелинейного
самосжатия (см. Самовоздействия света ).Наиб. благоприятные условия
для формирования С. реализуются в одномодовых волоконных световодах благодаря
предельно малым оптич. потерям (~0,2 дБ/км при длине волны излучения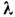 = 1,55 мкм) и устойчивости модовой структуры излучения при возрастании
входной мощности вплоть до значений, близких к порогу самофокусировки.
= 1,55 мкм) и устойчивости модовой структуры излучения при возрастании
входной мощности вплоть до значений, близких к порогу самофокусировки.
Временные эффекты самовоздействия (самосжатия) оптич. импульсов обусловлены
нелинейной добавкой к показателю преломления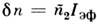 , где эфф. значение интенсивности
, где эфф. значение интенсивности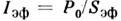 определяется отношением пиковой мощности импульса Р0 к
эфф. площади моды Sэф,
определяется отношением пиковой мощности импульса Р0 к
эфф. площади моды Sэф,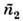 -
коэф. нелинейности (в кварцевых световодах
-
коэф. нелинейности (в кварцевых световодах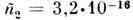 см2/Вт). При распространении импульса на расстояние z его вершина
приобретает дополнит. фазовый набег
см2/Вт). При распространении импульса на расстояние z его вершина
приобретает дополнит. фазовый набег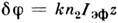 (k - волновое число) и, следовательно, зависящую от времени добавку к
несущей частоте
(k - волновое число) и, следовательно, зависящую от времени добавку к
несущей частоте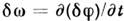 .
Т.о., в результате фазовой самомодуляции нарастает несущая частота от фронта
импульса к его хвосту, т. е. происходит частотная модуляция. Для скорости
частотной модуляции
.
Т.о., в результате фазовой самомодуляции нарастает несущая частота от фронта
импульса к его хвосту, т. е. происходит частотная модуляция. Для скорости
частотной модуляции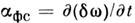 справедлива оценка
справедлива оценка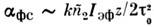 ,
где
,
где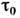 -
длительность импульса.
-
длительность импульса.
Другой конкурирующий процесс - дисперсионное расплывание импульса возникает
вследствие дисперсии групповой скорости, характеризуемой величиной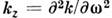 Спектрально-ограниченный импульс приобретает частотную модуляцию, скорость
к-рой
Спектрально-ограниченный импульс приобретает частотную модуляцию, скорость
к-рой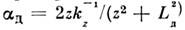 зависит от пройденного расстояния z, где
зависит от пройденного расстояния z, где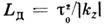 - дисперсионная длина. В спектральном диапазоне, соответствующем аномальной
дисперсии групповой скорости (
- дисперсионная длина. В спектральном диапазоне, соответствующем аномальной
дисперсии групповой скорости (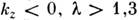 мкм), частота импульса уменьшается от фронта импульса к хвосту.
мкм), частота импульса уменьшается от фронта импульса к хвосту.
Из условия баланса конкурирующих процессов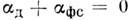 при прохождении импульсом расстояния
при прохождении импульсом расстояния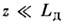 можно оценить критич. мощность, при к-рой формируется С.
можно оценить критич. мощность, при к-рой формируется С.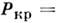
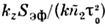
Основой для адекватного матем. описания процессов формирования
и взаимодействия С. пикосекундного диапазона длительностей является нелинейное
ур-ние Шрёдингера, к-рому удовлетворяет комплексная амплитуда поля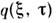 (см. Солитон ).Огибающая солитонного импульса имеет вид
(см. Солитон ).Огибающая солитонного импульса имеет вид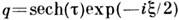 , где
, где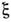 - расстояние, нормированное на дисперсионную длину
- расстояние, нормированное на дисперсионную длину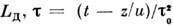 - бегущее время, нормированное на нач. длительность импульса, и - групповая
скорость. Нелинейное ур-ние Шрёдингера принадлежит к классу интегрируемых
нелинейных ур-ний и решается обратной задачи, рассеяния методом. Если
мощность спектрально-ограниченного импульса превышает критическую, то его
асимптотич. поведение при
- бегущее время, нормированное на нач. длительность импульса, и - групповая
скорость. Нелинейное ур-ние Шрёдингера принадлежит к классу интегрируемых
нелинейных ур-ний и решается обратной задачи, рассеяния методом. Если
мощность спектрально-ограниченного импульса превышает критическую, то его
асимптотич. поведение при определяется солитонной составляющей, амплитуда несолитонной части решения
убывает
определяется солитонной составляющей, амплитуда несолитонной части решения
убывает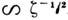
Важным классом аналитически вычисляемых решений нелинейного ур-ния Шрёдингера
являются N-солитонные импульсы, соответствующие нач. условиям вида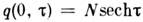 , где N - целое число. Они представляют собой нелинейную суперпозицию
N движущихся с одинаковой скоростью солитонов с амплитудами qm
= (2т - 1), т = 1, 2, .... N. Важные особенности N-солитонных
импульсов состоят в том, что их распространение начинается с самосжатия
(рис. 1), а модуль комплексной амплитуды периодичен по
, где N - целое число. Они представляют собой нелинейную суперпозицию
N движущихся с одинаковой скоростью солитонов с амплитудами qm
= (2т - 1), т = 1, 2, .... N. Важные особенности N-солитонных
импульсов состоят в том, что их распространение начинается с самосжатия
(рис. 1), а модуль комплексной амплитуды периодичен по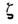 с периодом
с периодом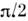
Закономерности формирования и распространения односолитонных и N-солитонных
импульсов были подтверждены экспериментами Л. Молленауэра (L. Mollenauer),
Р. X. Столена (R. H. Stolen) и В. Гордона (W. Gordon). В этих опытах с
помощью тщательно сформированных пикосекундных импульсов синхронно накачиваемого
лазера на центрах окраски (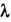 = 1,5 мкм; полная длительность импульса по полувысоте ~ 7 пкс;
= 1,5 мкм; полная длительность импульса по полувысоте ~ 7 пкс;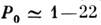 Вт) удалось наблюдать односолитонные и N-солитонные импульсы для N
Вт) удалось наблюдать односолитонные и N-солитонные импульсы для N 4.
Успешные эксперименты с С. стимулировали их применение в волоконно-оптич.
связи для сверхскоростной передачи информации, в технике формирования импульсов
фемтосекундной длительности, в спектроскопии быстропротекающих процессов
и привели к созданию солитонных лазеров.
4.
Успешные эксперименты с С. стимулировали их применение в волоконно-оптич.
связи для сверхскоростной передачи информации, в технике формирования импульсов
фемтосекундной длительности, в спектроскопии быстропротекающих процессов
и привели к созданию солитонных лазеров.
Теоретически и экспериментально исследовано влияние различных возмущающих факторов (оптич. потери, дисперсия высших порядков, инерционность нелинейного отклика, стохастич. возмущения формы входного импульса и параметров световода) на распространение пико- и фемтосекундных С. и на их взаимодействие. Показана возможность компенсации оптич. потерь за счёт комбинац. усиления, что позволяет реализовать передачу С. на расстояния до 50 км.
Распространение мощных когерентных импульсов света в резонансно-поглощающих средах (см. Самоиндуцированная прозрачность)также сопровождается солитонными эффектами. Если длительность импульса t0 существенно меньше времён релаксации населённостей T1 и затухания свободной поляризации Т2, то в результате поглощения в течение 1-й половины импульса и последующего усиления в течение 2-й половины импульса формируется стационарный волновой пакет, проникающий в среду на расстояние, существенно превышающее длину линейного поглощения (см. также Двухуровневая система).
Матем. описание этого процесса основывается на системе ур-ний Максвелла
- Блоха. Для спектрально-ограниченных импульсов осн. значение имеет площадь,
заключённая под огибающей:
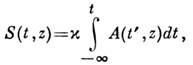
где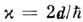 , d - дипольный момент резонансного перехода,
, d - дипольный момент резонансного перехода,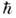 - постоянная Планка. Импульсы с площадью
- постоянная Планка. Импульсы с площадью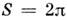 и огибающей
и огибающей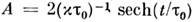 являются устойчивыми. Групповая скорость распространения импульса и меньше
скорости света. Характерное время задержки tзимпульса
на расстоянии L пропорционально коэф. линейного поглощения
являются устойчивыми. Групповая скорость распространения импульса и меньше
скорости света. Характерное время задержки tзимпульса
на расстоянии L пропорционально коэф. линейного поглощения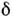 :
: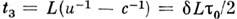 . Если площадь исходного импульса превышает
. Если площадь исходного импульса превышает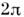 в
N раз, то в процессе распространения он разбивается на последовательность
N импульсов с разл. длительностями, амплитудами и скоростями (рис. 2).
в
N раз, то в процессе распространения он разбивается на последовательность
N импульсов с разл. длительностями, амплитудами и скоростями (рис. 2).
Солитонные эффекты проявляются при взаимодействии волновых пакетов с
разл. несущими частотами в средах с квадратичной нелинейностью ( т. н.
параметрические С.). В этом случае стационарный импульс формируется в результате
баланса процессов энергообмена и расстройки групповых скоростей. Теоретически
показана возможность формирования С. при вынужденном комбинац. рассеянии
света (ВКР-солитоны) и в процессе вынужденного Мандельштама - Бриллюэна
рассеяния, однако экспериментально они не наблюдались из-за ряда жёстких
требований на параметры излучения и среды.
Рис. 2. Разбиение -импульса
на три
-импульса
на три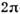 -импульса
при резонансном самовоздействии.
-импульса
при резонансном самовоздействии.

С. А. Ахманов, В. А. Выслоух
|
|