Глоссарий по физике

Устойчивость движения

Устойчивость движения - способность систем слабо менять (в том или ином смысле) своё состояние или свойства под действием возмущений. Теория устойчивости (У.) - это совокупность представлений и методов, обобщающих и формализующих разл. аспекты У. разнообразных систем. Наиб. распространёнными понятиями теории У. являются У. по Ляпунову, орбитальная У., асимптотическая У., структурная У.

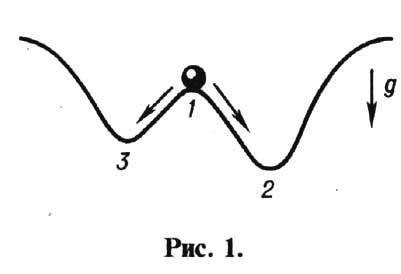
Наглядным примером, демонстрирующим нек-рые аспекты понятия У., является простейшая динамическая система: тяжёлый шарик на неровной поверхности (рис. 1); в точке 7 потенц. энергия шарика имеет максимум, и это положение равновесия неустойчиво: под действием малых возмущений шарик скатывается в более низкую точку (2 или 3), где его потенц. энергия имеет минимум. Если пренебречь трением, то шарик будет в течение бесконечного времени совершать колебания вблизи положения устойчивого равновесия (точек 2 и 3). Если шарик начнёт скатываться с точки, более низкой, чем точка I, то амплитуда колебаний будет меньшей (т. к. нач. энергия системы меньше). Однако близким нач. данным будут отвечать траектории с близкими периодами и амплитудами (орбитальная У.). В том случае, когда трение не мало, скорость шарика будет убывать и он остановится в точке устойчивого равновесия. Это состояние устойчиво асимптотически, в фазовом пространстве является притягивающим множеством. Если слабо деформировать поверхность, то характер движения не изменится (структурная У.).

Основные понятия. Пусть траектория L динамической системы задаётся отображением х(t) = Т^tх₀, где х-совокупность координат точки в фазовом пространстве системы, Т^t - оператор эволюции, преобразующий нач. состояние системы с координатами х₀ в состояние с координатами x(t)в момент времени t. Траектория L у с т о й ч и в а п о Л я п у н о в у, если для сколь угодно малого e можно найти такое d, что для любого нач. состояния 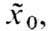близкого к x₀, т. е. 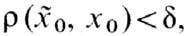всегда окажется 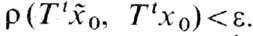Здесь r(x₁, x₂)- расстояние между точками х₁ и х₂ в фазовом пространстве. Если

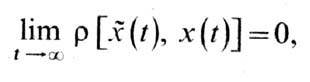
то У. наз. а с и м п т о т и ч е с к о й, а если к тому же

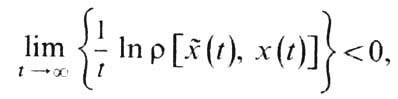
то У. наз. э к с п о н е н ц и а л ь н о й. Пусть L - нек-рая траектория системы,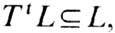 а 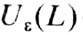-нек-рая её e-окрестность, т. е. r(x, L)<e для любой точки 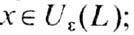здесь и ниже r(x, L)-расстояние от точки х до множества L в фазовом пространстве. Если для любого е можно найти такое d, что всякая траектория, начинающаяся в U_d(L), всегда остаётся в U_e(L), то траектория L наз. о р б и т а л ь н о (о р б и т н о) у с т о й ч и в о й. Если к тому же существует такое d₀ что при всех d<d₀ для любой траектории {x(t}}, начинающейся в U_d(L),

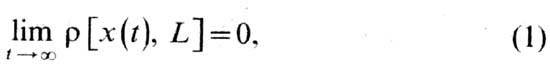
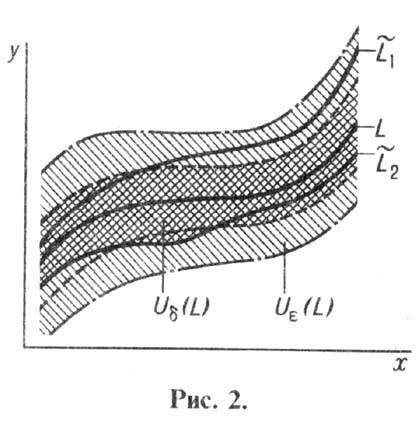
то траектория наз. а с и м п т о т и ч е с к и о р б и т а л ь н о у с т о й ч и в о й. Геом. смысл орбитальной устойчивости проиллюстрирован на рис. 2 (L- исходная, L^~₁ и L^~₂ - возмущённые траектории на фазовой плоскости {х, y}). Для У. по Ляпунову требуется также малость расстояния между одноврем. точками на близких траекториях (в указанном выше смысле). Из У. по Ляпунову следует У. орбитальная. Об-ратное, вообще говоря, не верно: две траектории могут быть сколь угодно близкими, а расстояние между двумя одноврем. точками на них может расти и стать немалым, даже если в нач. момент эти точки близки. Напр., для ур-ния Дуффинга (G. Duffing)

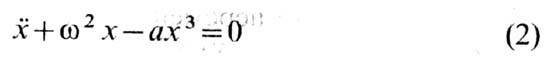
с нач. условиями

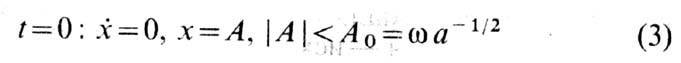
все траектории периодические. Период решения т растёт от 2pw до бесконечности по мере роста амплитуды А от нуля до А₀. При достаточно малых изменениях нач. условий траектории системы (2), (3) оказываются близкими. Однако благодаря зависимости периода решения от амплитуды близкие в нач. момент точки на двух соседних траекториях со временем разойдутся на большое расстояние. Поэтому при любых a>0 фазовые траектории системы устойчивы орбитально и неустойчивы по Ляпунову. В пределе a = 0 ур-ние (2) переходит в ур-ние гармонич. колебаний, период к-рых не зависит от амплитуды t=2p/w и все траектории оказываются устойчивыми по Ляпунову.

Если в ур-нии гармонич. колебаний учтено трение

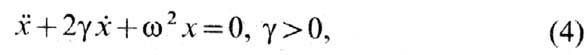
то такая система имеет асимптотически (экспоненциально) устойчивую траекторию: x=0, поскольку при любых нач. условиях r[x(t), 0]->0 при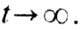

Асимптотически устойчивое множество траекторий L в фазовом пространстве динамич. системы наз. а т т р ак т о р о м, если оно: 1) компактно и неразложимо на отдельные структурные элементы; 2) инвариантно относительно Т^t: T^tL=L; 3) оператор T^t рекуррентен на L, т. е. для сколь угодно больших времён t₀>0 траектория y(t)= Т-х произвольной точки 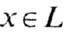при t>t₀ пройдёт в сколь угодно малой окрестности точки х. В случае замкнутых траекторий последнее требование означает беско-нечнократное прохождение системой каждой точки траектории, т. е. периодич. движение (в силу теоремы Коши; см. Коши задача). Примеры аттракторов: асимптотически устойчивые стационарные состояния [для ур-ния (4)-это точка x=0]; устойчивые предельные циклы; странные аттракторы (отвечающие стохастическим колебаниям в нелинейных диссипативных системах).

О б л а с т ь ю п р и т я ж е н и я D аттрактора L наз. множество всех нач. точек 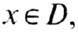для к-рых

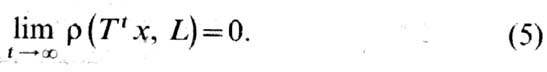
Для ур-ния (4) область притяжения аттрактора х= 0 совпадает со всем пространством.

Если автономная динамич. система x^.=f(x)имеет двумерное фазовое пространство, x={x₁, х₂}, то её состояния равновесия х = х_с определяются из системы ур-ний f(x) = 0. На фазовой плоскости {x₁, х₂} поведение траекторий в окрестности одного из состояний равновесия может иметь вид, показанный на рис. 3: состояния равновесия (а, в, д) - неустойчивые, (б, г) - асимптотически устойчивые, равновесие (е) - устойчивое, но не асимптотически.

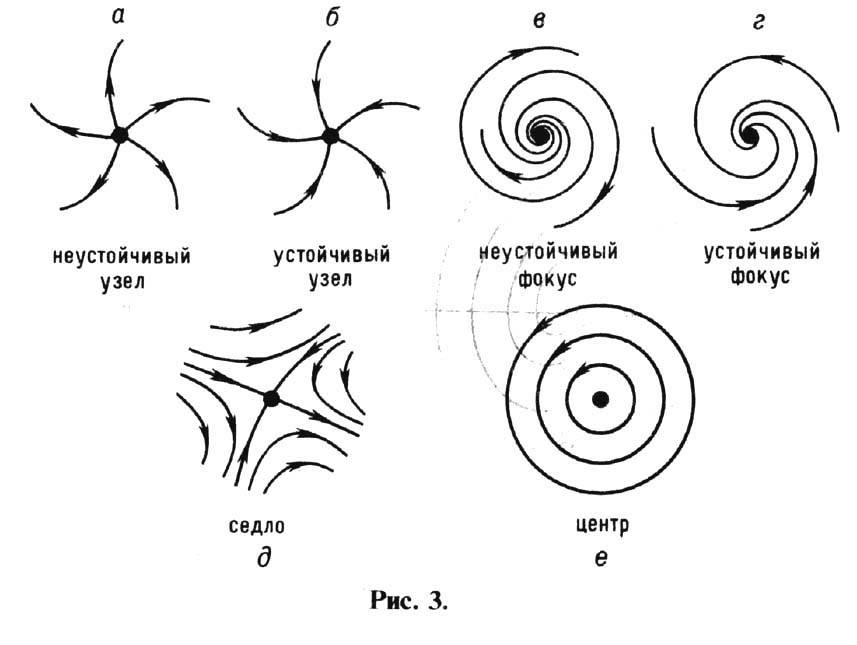
Если размерность фазового пространства больше чем 2, то наряду с указанными типами устойчивости могут появляться и более сложные, комбинир. типы (напр., седло - узел, узел-фокус и др.).

В ряде случаев динамич. система имеет большое число густорасположенных стационарных состояний. Такая ситуация реализуется, напр., когда тяжёлый шарик находится на горизонтальной плоскости. В каждой точке поверхности положение шарика устойчиво, причём нач. условия определяют то положение, какое установится в процессе эволюции. Напр., если сила трения качения пропорц. скорости, то изменение координаты шарика со временем описывается ур-нием

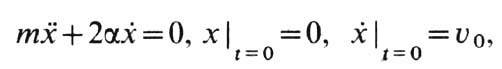
из к-рого следует

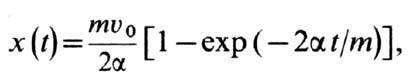
т. е. конечное положение 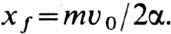Отсюда следует так-же, что перевести систему из одного стационарного сотояния x_f⁽¹⁾ в другое, близкое к первому, x_f⁽²⁾ можно помощью малого воздействия (возмущения). По отноше-нию к такого типа состояниям равновесия употребляется термин "безразличное равновесие".

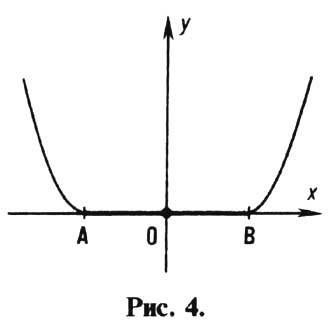
Несколько более сложная ситуация возникает в том случае, когда область (фазового) пространства, занима-емая безразличными состояниями равновесия, ограничена. Примером такой системы является шарик, находящийся в яме, дно к-рой - горизонтальная плоскость (рис. 4). При любых нач. условиях шарик в конце концов остановится в одной из точек дна ямы. Широкий класс систем, обладаю-щих аналогичными свойствами, может быть описан с помощью

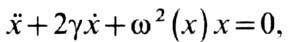
нелинейного дифференц. ур-ния в к-ром w²₀(x)=w²₀q(x²-x²₀)

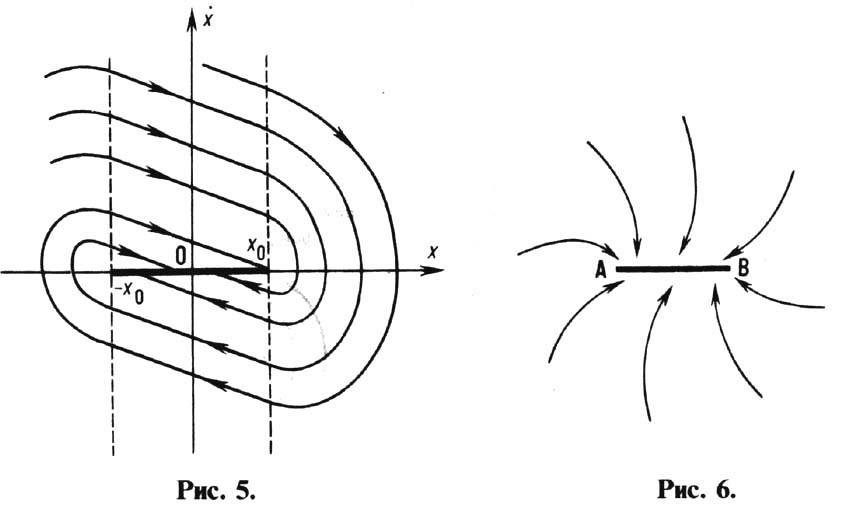
Здесь q(z)-единичная функция Хевисайда. Данная система имеет континуум стационарных состояний - х₀<х<х₀, каждое из к-рых устойчиво (безразличное равновесие). Фазовый портрет этой системы показан на рис. 5. Для этой и подобных систем характерно то, что стационарные состояния на нек-ром отрезке устойчивы (отрезок АВ на рис. 4; отрезок [ - х₀, х₀] на рис. 5), но свойством асимп-тотич. устойчивости обладает лишь весь отрезок в целом. Реализуемость конкретного состояния из отрезка зависит от нач. условий. В таких случаях говорят о притягивающем отрезке (рис. 6).

В ряде задач притягивающий отрезок формируется из конечного или счётного числа состояний равновесия, являющихся асимптотически устойчивыми. В этом случае соседние состояния часто отделены "барьером" и для перехода между ними требуется воздействие конечной (немалой) величины. Такая ситуация характерна для систем, описываемых дифференц. включениями, для распределённых систем и др.

Если система с малой диссипацией имеет один или неск. регулярных (нестохастических) аттракторов, причём её свойства вдали от аттракторов близки к свойствам К-систем (т. е. систем, обладающих локальной неустойчивостью и перемешиванием траекторий), то под действием возмущений система будет периодически отбрасываться от аттракторов и вдали от них длит. время будет вести себя подобно K-системе. В результате длительные периоды времени, когда система ведёт себя, как K-система, перемежаются периодами, когда её поведение регуляризуется (из-за притяжения к аттракторам). В этом случае говорят, что система имеет к в а з и а т т р а к т о р ы.

Иногда термин "квазиаттрактор" применяют к системе, к-рая имеет большое число асимптотически устойчивых стационарных состояний, причём соседние состояния отделены одно от другого достаточно низким барьером. Под действием случайных возмущений система будет перемещаться между разл. состояниями, оставаясь постоянно в окрестности притягивающего множества М (составленного из отдельных стационарных состояний). Если возмущение окажется немалым и система уйдёт далеко от M, то вследствие асимптотической устойчивости компонентов М она вернётся в окрестность М. При наличии такого квазиаттрактора фазовые траектории системы притягиваются к нему, а затем под действием шумов начинается случайное блуждание между его компонентами. Квазиаттракторы иногда обнаруживаются при численном исследовании нелинейных динамич. систем (без флуктуации), где роль шумов играют погрешности вычислит. процедуры.

Для исследования У. обычно применяют два метода Ляпунова. П е р в ы й (или п р я м о й) метод основан на построении функции (функционала) Ляпунова. Напр., для ур-ния нелинейного осциллятора с трением

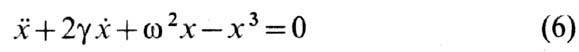
можно использовать следующую функцию Ляпунова:

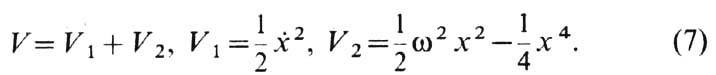
Эта величина имеет смысл полной энергии системы: слагаемое V₁ есть кинетическая, а V₂ - потенц. энергия. Производная по времени от V с учётом ур-ния (6) есть

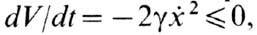
т. е. V убывает на любой траектории системы, кроме тех, к-рые отвечают стационарным состояниям (x=-w. 0, +w) Потенц. энергия имеет максимум V₂=w⁴/4 при |x|=w. Поэтому для всех нач. условий

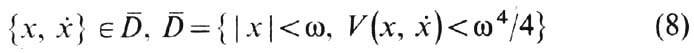
ни одна из траекторий не выйдет за пределы D^- (иначе это повлекло бы рост, а не убывание V). Следовательно, система приближается к единственному стационарному состоянию в области D, где V достигает минимума V=0, т. е. к х=0. Это состояние асимптотически устойчиво.

В т о р о й метод - исследование устойчивости по линейному приближению. Напр., линеаризация (6) вблизи стационарных решений х_с даёт

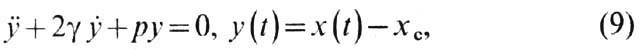
где p=w²>0 для x_c=0 и p=w²>0 для x_c= +w Отсюда следует, что решение х_с = 0 экспоненциально устойчиво, а решения x_c= +w неустойчивы (как седловые особые точки).

У. п о ч а с т и п e р е м е н н ы х. Пусть система характеризуется n-мерным фазовым пространством S_n = {x_i | i=1, ..., n, n>1}. Точка х = 0 устойчива по отношению к переменным х₁ ..., x_k, если она устойчива по Ляпунову в k-мерном подпространстве S_k = {x_i|i=1, ...,k, k<n} в соответствии с определением устойчивости, приведённым выше.

Близость к нулю переменных x_k+1, ..., х_n не требуется.

С т р у к т у р н а я у с т о й ч и в о с т ь (г р у б о с т ь) - свойство динамич. системы сохранять структуру фазового пространства при малых возмущениях (изменениях системы). Пусть А и 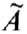-исходная и возмущённая системы. Система А наз. грубой, если для любого e найдётся такое d что если системы А и 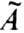отстоят друг от друга менее чем на d(в метрике С¹), то найдётся отображение (гомеоморфизм) 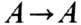^~ , сдвигающее точки менее чем на e и преобразующее траектории невозмущённой системы в траектории возмущённой. Понятие грубости введено А. А. Андроновым и Л. С. Понтрягиным. Матем. аппарат, позволяющий исследовать структурную У.,- это катастроф теория, методами к-рой определяются области грубости системы и устанавливаются закономерности перестройки структуры фазового пространства при переходе через бифуркац. значения параметров (см. Бифуркация).

У. п о Л а г р а н ж у - свойство динамич. системы оставаться в ходе эволюции в огранич. области фазового пространства.

У. п о П у а с с о н у (возвращаемость) - свойство динамич. системы возвращаться в ходе эволюции сколь угодно близко к своему нач. положению (в фазовом пространстве) по истечении сколь угодно большого времени (см. Пуанкаре теорема, Эргодическая теория).

У. у с л о в н а я-У. по отношению не к произвольным возмущениям, а только по отношению к тем, к-рые подчинены определ. ограничениям.

У. с и с т е м с д и с к р е т н ы м в р е м е н е м. Пусть имеется нек-рая последовательность {х_n}, задаваемая рекуррентным соотношением

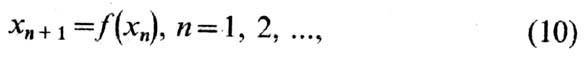
где х_п-k-компонентный вектор, x_n = (x_n1,..., x_nk). К такому виду может быть приведено описание мн. динамич. систем с непрерывным временем; в случае (10) в роли времени выступает номер члена последовательности. На такие системы естеств. образом переносятся все приведённые определения У.

Пусть х_n- однокомпонентная величина (k=1)и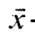-неподвижная точка отображения (10),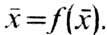 Точка х^- асимптотически устойчива, если в ней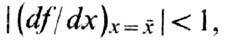и неустойчива, если знак неравенства противоположный. Тем самым асиптотическая У. неподвижной точки х эквивалентна сходимости итерационного процесса (10) решения ур-ния x-f(x) = 0.

У. п о о т н о ш е н и ю к к о н е ч н ы м в о з м у щ е н и я м. Пусть система обладает N устойчивыми состояниями {S_i}, т. е. имеет место мультистабильность (при N=2 - биста-бильность). Каждое из устойчивых состояний S_i, i=1, ..., N обладает нек-рой областью притяжения D(S_i). Любое возмущение, не выводящее систему из D(S_i), входит в класс тех возмущений, по отношению к к-рым состояние S_i устойчиво. Наоборот, состояние S_i неустойчиво по отношению к возмущениям всякий раз, когда эти возмущения переводят систему из D(S_i)в D(S_j)при 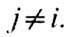Эти возмущения заведомо конечны (не могут быть сколь угодно малыми), поскольку для любой пары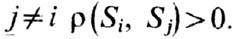 Напр., для инициирования горения необходимо, чтобы очаг имел достаточно высокую температуру и большие размеры. При этом условии система переходит из низкотемпературного режима протекания экзотермич. реакции в высокотемпературный.

У. р а с п р е д е л ё н н ы х с и с т е м. Такие системы в общем случае характеризуются бесконечным числом степеней свободы и бесконечномерным (во многих случаях - счётномерным) фазовым пространством.

Для определения типа У. применяют методы Ляпунова (см. выше), модифицированные применительно к специфике распределённых систем. Напр., для краевой задачи

т. е. функционал V(u)монотонно убывает и ограничен снизу, а его производная dV/dt обращается в нуль только на стационарных решениях задачи (11). Поэтому из любых нач. состояний система переходит к нек-рому устойчивом стационарному состоянию. Задача (11) при b<k₀⁴ имеет единственное однородное решение: и = 0. Кроме того, пр. 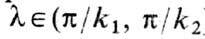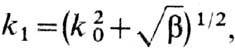b>0 и достаточно больших R она имеет неоднородные пространственно-периодические стационарные решения (при b<k₀⁴ их периоды лежат в интервале 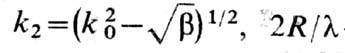- целое]. Выяснить, какие из этих решении устойчивы, можно с помощью второго метода Ляпунова. Для этого следует линеаризо-вать (11) в окрестности изучаемого стационарного реше-ния и_с(х)и, полагая малое возмущение равным u(x, t) 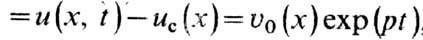, найти спектр собств. значе-ний краевой задачи:

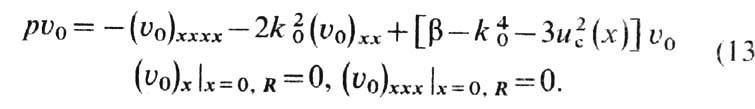
В частности, если u_с(x) = 0, то

где q - волновой вектор возмущения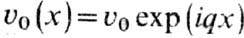 пробегающий дискретный ряд значений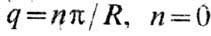 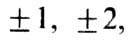... Следовательно, при все возмущения за-тухают, причём b<0

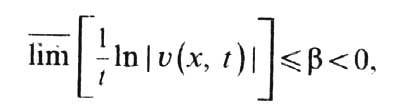
т. е. решение и_с(х) = 0 устойчиво экспоненциально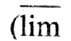означает верх. предел). Наоборот, при b>0 и достаточно больших R в область p>0 попадает группа допустимых волновых векторов q, так что соответствующие возмущения экспоненциально растут. Следовательно, решение и_с(х) = 0 неустойчиво. Исследование У. неоднородных стационарных решений выполняется с помощью теории линейных дифференц. ур-ний с периодич. коэф. и показывает, что из всех стационарных решений при b<<k₀⁴ устойчивы только решения с периодами ,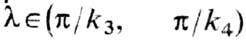

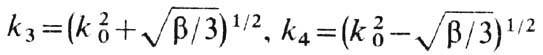
B более общем случае пусть система описывается связанными нелинейными ур-ниями диффузионного типа:

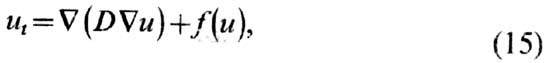
где u = (u₁ ..., u_n), f(u)= (f₁(u), ...,f_n(u)), D - nхn-матрица, зависящая от и. Пусть и_с = 0 стационарное решение (15), f(0) = 0. Линеаризация (15) в окрестности и_с позволяет получить характеристическое ур-ние:

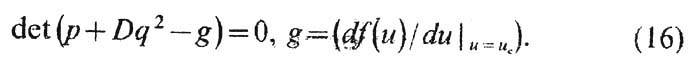
Система наз. а б с о л ю т н о н е у с т о й ч и в о й, если ур-ние (16) имеет решения с Re p> 0 при q=0 (т. е. каждая точка среды может самовозбуждаться в отсутствие диффузионного взаимодействия между соседними точками). В частности, если в область Re p>0 попадает чётное число корней ур-ния (16), то неустойчивость наз. к о л е б а т е л ь н о й. Если возникновение неустойчивости обусловлено диффузией, т. е. среда локально устойчива, пока не включено взаимодействие между соседними её элементами, то неустойчивость наз. д и ф ф у з и о н н о й. Формально это значит, что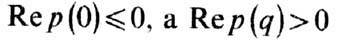 только в нек-рых интервалах значений |q|>0. В примере (11), (14) неустойчивость однородного состояния является диффузионной, Диффузионную неустойчивость в двухкомпонентной системе (15) с диагональной матрицей D иногда наз. т ь ю р и н г о в-с к о й (А. М. Turing, 1952).

Если двухкомпонентная система (15) колебательно неустойчива, то при D = 0 в ней могут возникать простые автоколебания. При 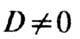могут появляться более сложные нестационарные режимы - вплоть до стохастических. Поскольку происхождение этих режимов связано с диффузией, их наз. диффузионным хаосом.

Литература по устойчивости движения

1. Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 3 изд., М., 1981;
2. Меркин Д. П., Введение в теорию устойчивости движения, 3 изд., М., 1987;
3. Бутенин Н. В., Неймарк Ю, И., Фуфаев Н. А., Введение в теорию нелинейных колебаний, 2 изд., М., 1987;
4. Постон Т., Стюарт Т., Теория катастроф и ее приложения, пер. с англ., М., 1980;
5. Ланда П. С., Автоколебания в распределенных системах, М., 1983;
6. Математическое моделирование. Процессы в нелинейных средах, под ред. А. А. Самарского и др., М., 1986;
7. Заславский Г. М., Сагде-ев Р. 3., Введение в нелинейную физику, М., 1988.

Н. А. Кириченко

к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  

Знаете ли Вы, что релятивизм (СТО и ОТО) не является истинной наукой? - Истинная наука обязательно опирается на причинность и законы природы, данные нам в физических явлениях (фактах). В отличие от этого СТО и ОТО построены на аксиоматических постулатах, то есть принципиально недоказуемых догматах, в которые обязаны верить последователи этих учений. То есть релятивизм есть форма религии, культа, раздуваемого политической машиной мифического авторитета Эйнштейна и верных его последователей, возводимых в ранг святых от релятивистской физики. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА Рыцари теории эфира

10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.