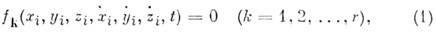
Неголономная система - моханич. система, на к-рую кроме геом. связей наложены ещё дифференциальные (кинематич.) связи,
не сводящиеся к геометрическим и называемые неголономными (см. Голономная
система). Математически неголономные связи выражаются ур-ниями вида:
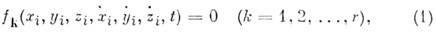
где хi, yi, zi - координаты,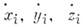 
- проекции скоростей, t - время, r - число наложенных связей.
При этом предполагается, что ур-ния (1) не могут быть непосредственно проинтегрированы;
в противном случае получим голо номную систему. Число координат xi,
yi, zi, определяющих положение H. с., больше
числа степеней свободы системы. T. к. ур-ния (1) непосредственно не интегрируются,
для H. с., в отличие от голономной, нельзя заранее выразить зависимые координаты
через независимые.
H. с. наз. линейной, если ур-ния (1) линейны
относительно скоростей, т. е. имеют вид:
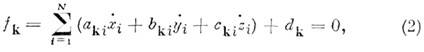
где а, b, с и d - функции xi,
yi, zi и t ; N - число точек системы.
Пример линейной H. с.- шар, катящийся по шероховатой
плоскости. Ур-ние связи, выражающее тот факт, что точка касания шара имеет скорость,
равную нулю, не может быть проинтегрировано. Возможные перемещения точек системы
при связях (2) удовлетворяют условиям:
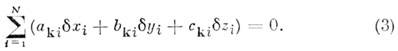
Движение линейных H. с. можно изучать с помощью
Чаплыгина уравнений, Аппеля уравнений и др. С учётом условий (3) эти
ур-ния могут быть получены из дифференциальных принципов (Д-Аламбера - Лагранжа
принцип и Гаусса принцип)или же из обобщённого интегрального принципа
Гамильтона - Остроградского.
H. с. наз. нелинейной, если ур-ния (1) нелинейны
относительно скоростей. Пример: система двух точек М(х, у, z)и M1(x1,
y1, z1), в к-рой точка M1
движется по заданному закону, а скорость точки M зависит от взаимного
расположения точек, напр. от расстояния MM1. Ур-ние
связи будет
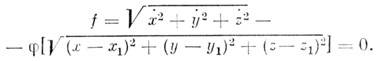
Ур-ния движения нелинейных II. с. могут быть
получены из тех же принципов механики, что и для линейных H. с., если возможные
перемещения точек системы удовлетворяют условию Четаова:
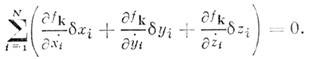
Механика H. с. находит приложения при решении
ряда задач совр. техники (автоматика, кибернетика и др.). Лит.: Чаплыгин С. А., Исследования по динамике него-лономных систем, M.- Л., 1949;
Герц Г., Принципы механики, изложенные в
новой связи, пер. с нем., M., 1Я59; Добронравов В. В., Основы механики неголономных
систем, M., 1970. Г. С. Погасав.
НЕЕЛЯ СТЕНКА - область между соседними
домона-ми (см. Магнитная доменная структура)в тонких магнитных плёнках, в к-рой быстрое пространств. изменение намагниченности M
происходит в плоскости расположения векторов намагниченности доменов (в
плоскости, параллельной поверхности плёнки). Согласно определению, в H. с.,
в отличие от Блоха стенки, divM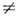 
0. Представление о доменных стенках (ДС) подобного типа впервые было введено
JI. Неелем (L. Neel, 1955) [1].
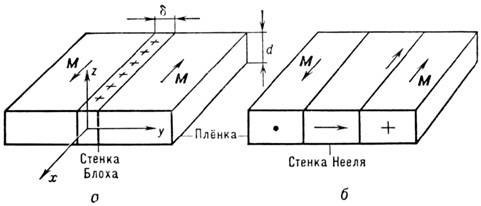
Причину образования H. с. удобно объяснить, используя рисунок. Если в топкой плёнке толщиной d при переходе от левого домена к правому (рис., а) намагниченность M вращается так, что остаётся параллельной плоскости ДС (стенка Блоха, плоскость xz), то в узкой полоске шириной d (толщина ДС) на поверхности плёнки образуются магнитостатич. заряды, приводящие к увеличению полной энергии стенки [2]. Эта энергия при условии d < d может быть снижена, если поворот M будет осуществляться в плоскости плёнки, как изображено на рис., б (стенка Нееля). С этим снижением полной энергии плёнки и связана энергетич. выгодность образования H. с. в тонких плёнках. По совр. оценкам, критич. толщина плёнки dкp, ниже к-рой выгодно образование H. с. в тонких плёнках, составляет сотни ангстрем.
Б. H. Филиппов
|
|
 |
