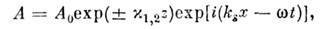
Поверхностные оптические волны (поверхностные поляритоны) - поверхностные эл--магн. волны оптич. диапазона, распространяющиеся вдоль границы раздела двух сред и существующие одновременно в них обеих. Поля, переносимые этими волнами, локализованы вблизи поверхности и затухают по обе стороны от неё. П. о. в. являются частично продольными электромагнитными волнами ТМ-типа: магн. вектор Н, перпендикулярный направлению распространения П. о. в., лежит в плоскости поверхности; электрич. вектор имеет две составляющие: Ех - вдоль волнового вектора ks и Еz - перпендикулярно поверхности (рис. 1, в). П. о. в. описываются ур-ниями Максвелла со стандартными граничными условиями. Распределение каждой из компонент (А)электрич. и магн. полей иа частоте w в плоской П. о. в., бегущей вдоль оси х (рис. 1, а), имеет вид
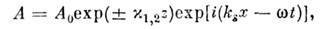
где А0 - амплитуда,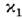 >0,
>0,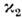 >0
- коэф. затухания П. о. в. в средах 1 и 2, t - время. Знак (+) относится
к среде 1 (z<0), ( - ) - к среде 2 (z>0) (рис. 1,6).
>0
- коэф. затухания П. о. в. в средах 1 и 2, t - время. Знак (+) относится
к среде 1 (z<0), ( - ) - к среде 2 (z>0) (рис. 1,6).
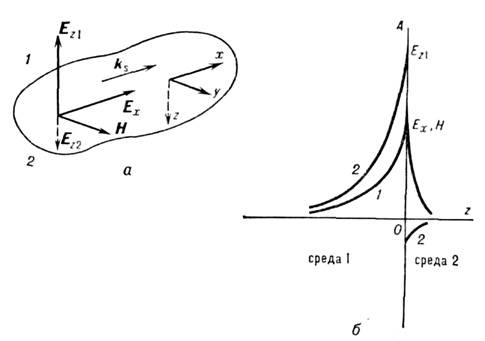
Рис. 1. Поверхностные оптические волны: а - ориентация электрического и магнитного векторов в поверхностной оптической волне, бегущей вдоль поверхности в направлении оси х; б - распределение полей в поверхностной оптической волне в плоскости, перпендикулярной направлению распространения. 1 - для компонент Ех и Н11=Н, изменяющихся при z= 0 непрерывно; 2 - для компоненты Еz, испытывающей при z = 0 скачок.
При заданной амплитуде магн. вектора А0 -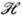 амплитуды
остальных компонент равны:
амплитуды
остальных компонент равны:
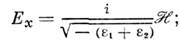
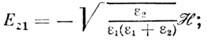
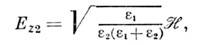
где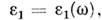
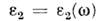 - диэтектрич. проницаемости сред 1 и 2 на частоте
- диэтектрич. проницаемости сред 1 и 2 на частоте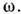 Волновой вектор ks удовлетворяет дисперсионному соотношению
Волновой вектор ks удовлетворяет дисперсионному соотношению
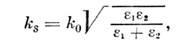
где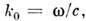 с - скорость света в вакууме. Коэф. затухания
с - скорость света в вакууме. Коэф. затухания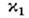 и
и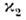 определяются
как
определяются
как
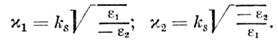
Из условия вещественности и положительности
величин ks,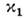 и
и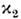 следует, что П. о. в. могут существовать только на границе раздела двух
сред с диэлектрич. проницаемостями разных знаков. Если в среде 1
следует, что П. о. в. могут существовать только на границе раздела двух
сред с диэлектрич. проницаемостями разных знаков. Если в среде 1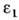 > 0, то диэлектрич. проницаемость среды 2, т. и. поверхностно-активной
среды (ПАС), должна удовлетворять условию
> 0, то диэлектрич. проницаемость среды 2, т. и. поверхностно-активной
среды (ПАС), должна удовлетворять условию
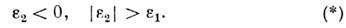
Обычно П. 0. в. возбуждают на границе ПАС
с воздухом (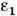 = 1) или др. прозрачным диэлектриком. Для металлов и легиров. полупроводников
с высокой концентрацией свободных носителей неравенство (*) выполняется
в области аномальной дисперсии диэлектрич. проницаемости, к-рая занимает
весь ИК- и видимый (для металлов) диапазон частот и ограничена сверху частотой
поверхностного плазмона
= 1) или др. прозрачным диэлектриком. Для металлов и легиров. полупроводников
с высокой концентрацией свободных носителей неравенство (*) выполняется
в области аномальной дисперсии диэлектрич. проницаемости, к-рая занимает
весь ИК- и видимый (для металлов) диапазон частот и ограничена сверху частотой
поверхностного плазмона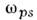 (для частот
(для частот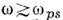 металл становится прозрачным и П. о. в. не возбуждаются, см. Металлооптика ).На
рис. 2 показана типичная дисперсионная кривая
металл становится прозрачным и П. о. в. не возбуждаются, см. Металлооптика ).На
рис. 2 показана типичная дисперсионная кривая для П. о. в. на металле, или поверхностных плазмон-поляритонов (параметры
для П. о. в. на металле, или поверхностных плазмон-поляритонов (параметры и ks нормированы соответственно на плазменную частоту
электронов
и ks нормированы соответственно на плазменную частоту
электронов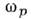 и k0).
и k0).
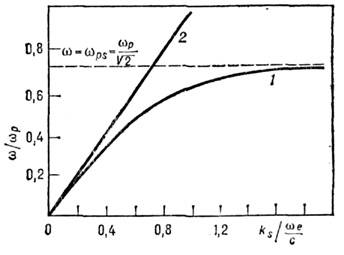
Рис. 2. Дисперсионная кривая поверхностных
плазмон-поляритонов (1) на плоской границе раздела между простым металлом
и вакуумом;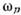 - плазменная частота электронов; 2 - световая линия
- плазменная частота электронов; 2 - световая линия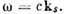
П. о. в. могут также возбуждаться на поверхности
полупроводников и диэлектриков в среднем ИК-диапазоне, в интервале между
частотами продольного и поперечного оптич. фононов, где диэлектрич. проницаемость
испытывает аномальную дисперсию. Соответствующие П. о. в. наз. также поверхностными
фонон-поляритонамн. Существуют П. о. в. и в области экситонного поглощения
на полупроводниках.
Разработано неск. эффективных методов
возбуждения П. о. в. светом (рис. 3): призменный, решёточный и с помощью
краевых диафрагм.
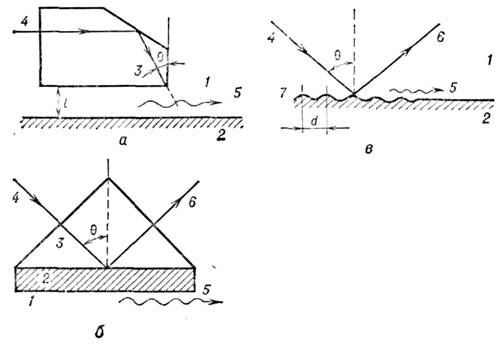
Рис. 3. Возбуждение поверхностных оптических
волн светом: а - прнзменный метод, геометрия Отто; б - призменный
метод, геометрия Кречманна; в - решёточный метод.
1 - диэлектрик
(воздух); 2 - ПАС (металл); 3 - призма;
4 - падающее
излучение; 5 - поверхностная оптическая волна;
6 - зеркально
отражённое излучение; 7 - решётка; l - зазор размером ~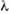 ;
d
- период решётки.
;
d
- период решётки.
В призменном методе, существующем в двух
модификациях (геометрия Отто, рис. 3, а и геометрия Кречманна, рис.
3, б), используется явление нарушенного полного внутреннего отражения при падении р-поляризованного излучения (поляризованного в плоскости
падения) со стороны оптически более плотной среды под углом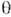 >arcsin
>arcsin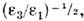 где
где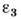 >
>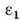 - диэлектрич. проницаемость материала призмы. В этом случае П. о. в. возбуждаются
на гладкой поверхности, где непосредственно это осуществить нельзя, т.
к. волновой вектор П. о. в. больше волнового вектора света k0
на той же частоте (рис. 2). При решёточном методе (рис. 3, в)П.
о. в. возбуждаются в
- диэлектрич. проницаемость материала призмы. В этом случае П. о. в. возбуждаются
на гладкой поверхности, где непосредственно это осуществить нельзя, т.
к. волновой вектор П. о. в. больше волнового вектора света k0
на той же частоте (рис. 2). При решёточном методе (рис. 3, в)П.
о. в. возбуждаются в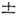 1-м порядке дифракции падающего р-поляризованного излучения на решётках
с периодом
1-м порядке дифракции падающего р-поляризованного излучения на решётках
с периодом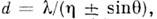 где
где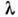 - длина волны излучения,
- длина волны излучения,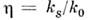 - эфф. показатель преломления границы раздела для П. о. в. В большинстве
случаев источниками падающего излучения при возбуждении П. о. в. являются
лазеры. Эффективность преобразования падающего объёмного излучения в П.
о. в. в ИК-области достигает десятых долей, а в геометрии Кречманна для
видимого света практически доходит до 1. Обратное преобразование П. о.
в. в объёмное излучение также возможно с помощью призм и решёток.
- эфф. показатель преломления границы раздела для П. о. в. В большинстве
случаев источниками падающего излучения при возбуждении П. о. в. являются
лазеры. Эффективность преобразования падающего объёмного излучения в П.
о. в. в ИК-области достигает десятых долей, а в геометрии Кречманна для
видимого света практически доходит до 1. Обратное преобразование П. о.
в. в объёмное излучение также возможно с помощью призм и решёток.
Исследование и применение П. о. в. является
перспективным и быстро развивающимся разделом оптики и спектроскопии твёрдого
тела. Это обусловлено уникальными свойствами П. о. в., к-рые при распространении
вдоль поверхности сосредоточены в ПАС в том же слое, что и объёмное излучение
той же частоты (напр., в скин-слое металла толщиной 10-6 - 10-5
см). Длина пробега П. о. в. вдоль поверхности в ИК-области спектра может
достигать неск. см и весьма чувствительна к процессам в поглощающем слое,
к состоянию поверхности и её изменениям, наличию адсорбиров. слоев, плёнок,
шероховатости и др. Это позволяет использовать метод возбуждения П. о.
в. для исследования поверхности и границ раздела, а также для оптич. измерений,
напр. измерения поглощения металлич. зеркал на уровне 0,01 с точностью
до 10%. Интерес к П. о. в. и др. поверхностным эл--магн. возбуждениям связан
также с тем, что в процессе лазерных воздействий на НАС обнаружены последствия
их генерации. Среди них: гигантское комбииац. рассеяние адсорбпров. молекулами;
усиленная генерация второй гармоники при отражении света от металлов; образование
поверхностных периодич. структур и рост эффективного коэф. поглощения при
нагреве металлов и полупроводников линейно поляризов. лазерным излучением;
возбуждение ТЕ-поляритонов на границе линейной и нелинейной сред и др.

М. Н. Либенсон
|
|