к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Самовоздействие волн

Самовоздействие волн - изменение характеристик волнового процесса вследствие инициируемых им разл. нелинейных явлений в среде. В узком смысле термин «самовоздействие волн» применяется к однокомпонентным системам с безынерционной нелинейностью. Рассмотрим, напр., ур-ние для простых волн:

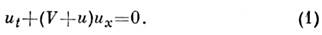
Решение этого ур-ние задаётся неявным соотношением: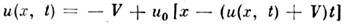 с нач. условием 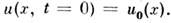пока нелинейные эффекты малы, 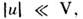это решение принимает вид: 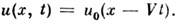Следовательно, волна распространяется без искажения формы и с пост. групповой скоростью V. В общем случае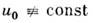 решение Яоши задачи для ур-ния (1) существует только в течение конечного времени: рост нелинейности (слагаемого ии_х)ведёт к деформации профиля волны, а в дальнейшем - к её опрокидыванию. Аналогично в случае нелинейного ур-ния теплопроводности

при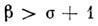 решение существует конечное время (т. н. время обострения), в течение к-рого возникает локализованная структура с убывающей шириной и неограниченно растущей амплитудой.

Как правило, в физ. задачах конечность времени существования или неограниченный рост решения связаны с пренебрежением к--л. эффектами. Если, напр., учесть диссипативные процессы, добавив в правую часть (1) слагаемое аи_хх, а > 0:

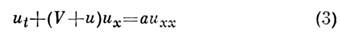
(Бюргерса уравнение ),то в этом случае конкуренция нелинейного увеличения крутизны профиля и его диссипативного сглаживания может давать решения с неизменным во времени профилем - ударную волну с конечной толщиной фронта. Кроме того, возникнут решения с убывающей амплитудой.

В примерах (1), (2) самовоздействие волн вело к эффектам типа опрокидывания фронта или к обострению профиля. Однако в ряде случаев именно нелинейные процессы ограничивают развитие неустойчивости. Напр., обобщённое ур-ние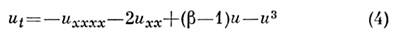

при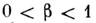 имеет единственное однородное решение: и = 0, к-рое неустойчиво по отношению к возмущениям типа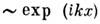 с волновыми векторами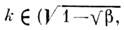 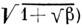. Самовоздействие волн, описываемое слагаемым (-u³) в (4), ограничивает рост амплитуды возмущений, и в системе устанавливается стационарная пространственно-пе-риодич. структура.

Строго говоря, однокомпонентные системы с самовоздействнем - это приближённое описание многокомпонентных систем, в к-рых характерные времена эволюции разл. степеней свободы сильно различаются. Напр., в нелинейной оптике безынерционная нелинейность для сильной световой волны формируется быстрыми по-ляризац. процессами в среде, инциируемыми самой световой волной. В общем случае временем задержки отклика среды на волновой процесс пренебрегать нельзя. При этом говорят об инерционной нелинейности или о нелинейной многокомпонентной системе. Пример - ур-ние Курамото - Цудзуки (двухкомпонентная система):

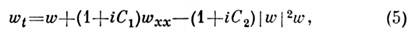
описывающее поведение многих систем в окрестности бифуркац. значений параметров (см. Бифуркация ).Здесь w - комплекснозначная функция, а С₁ и С₂ - действительные числа. При подходящем выборе коэффициентов ур-ние (5) допускает как простейшие, стационарные решения, так и более сложные, вплоть до стохастических (т. н. диффузионный хаос ).Конкуренция диссипативных процессов и эффектов самовоздействия волн (в указанном смысле) ведёт к усложнению динамики системы. Физ. пример инерционного самовоздействия волн - тепловая дефокусировка лазерного излучения, обусловленная изменением показателя преломления среды при её нагреве излучением (см. Самодефокусировка света).

Литература по самовоздействию волн

Качмарек Ф., Введение в физику лазеров, пер. с польск., М., 1981;
Математическое моделирование. Сб. ст., М., 1986;
Васильев В. А., Романовский Ю. М., Яхно В. Г., Автоволновые процессы, М., 1987;
Заславский Г. М., Сагдеев Р. 3., Введение в нелинейную физику, М., 1988.

Н. А. Кириченко

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что "гравитационное линзирование" якобы наблюдаемое вблизи далеких галактик (но не в масштабе звезд, где оно должно быть по формулам ОТО!), на самом деле является термическим линзированием, связанным с изменениями плотности эфира от нагрева мириадами звезд. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира