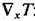к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Термогальваномагнитные явления

Термогальваномагнитные явления - явления переноса теплоты и зарядов в проводнике, происходящие при одноврем. воздействии электрич. и магн. полей, а также градиента температуры. Одновременно наличие этих трёх факторов приводит не только к изменению кинетич. коэф., характеризующих проводник: коэф. теплопроводности к, коэф. Холла R (см. Холла эффект ),проводимости s, коэф. термоэдс a, но и к появлению "перекрёстных" явлений. К последним относятся поперечный и продольный Нернста - Эттингсхаузена эффекты, Нернста эффект, Эттингсхаузена эффект, а также эффекты, обусловленные влиянием магн. поля на термоэлектрические явления и воздействием градиента температуры (или потока теплоты) на гальвано магнитные явления. Т. я. могут наблюдаться в полупроводниках, металлах, полуметаллах, плазме и др. При феноменология, описании Т. я. обычно пользуются системой ур-ний, в к-рой поток теплоты q и электрич. поле E выражены через плотность тока j, разность потенциалов f и градиент температуры :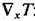

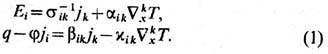
Тензоры s_ik^-1, 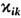, a_ik,b_ik, согласно соотношению симметрии кинетич. коэф. в магн. поле (см. Онсагера теорема ),удовлетворяют соотношениям

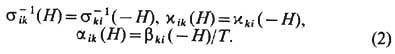
Для изотропного проводника ур-ния (1), (2) приводят к двум векторным ур-ниям

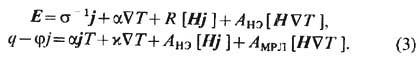
Ур-ния (3) содержат 6 независимых скалярных кинетич. коэф., зависящих от магн. поля H: s, 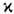, a, а также R, А_НЭ, A_МРЛ - коэф., характеризующие эффекты Холла, Нернста-Эттингсхаузена и Маджи-Риги-Ледюка эффект.

В металлах и вырожденных полупроводниках перенос заряда и тепла осуществляется носителями заряда с энергиями вблизи энергии Ферми 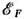в узком слое kT. Поэтому величины всех коэф. малы, порядка 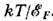В полупроводниках с двумя сортами носителей заряда (электронами и дырками) существенный вклад в Т. я. вносит биполярное движение электронов и дырок, поэтому все кинетич. коэф. Т. я. содержат составляющую, пропорц. 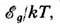где 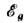- ширина запрещённой зоны полупроводника, и, т, о., все коэф. в (3) возрастают.

Обычно с помощью (3) Т. я. в изотропном проводнике классифицируются след. образом: ось z выбирают вдоль H и различают продольные (j_x=j_v = 0, q_x = q_y = 0)и поперечные 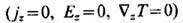эффекты. При этом Т. я. подразделяют на изотермические 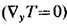и адиабатические (q_у = 0; см. табл.).

Поперечные термогальваномагннтные явления ( и - изотермические, а-адиабатические)

Коэф. А_РЛ и А_Э характеризуют соответственно Риги - Ледюка эффект и Эттингсхаузена эффект.

Указанные в табл. кинетич. коэф. связаны между собой со отношениями

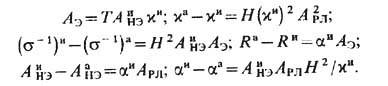
По определению, эффекты Эттингсхаузена и Риги - Ледюка могут быть только адиабатическими, остальные Т. я. могут быть как изотермическими, так и адиабатическими. Обычно измерения коэф. Т. я. выполняются в калоримет-рич. приборах, когда условия эксперимента близки к адиабатическим. Однако если фононная часть теплопроводности значительно больше электронной, то адиабатич. коэф. практически совпадают с изотермическими.

Коэф., характеризующие Т. я., зависят от механизма рассеяния носителей заряда и чувствительны к зависимости времени релаксации импульса т носителей заряда (времени свободного пробега) от их энергии. Кроме того, на эти коэф. влияют зонная структура энергетич. спектра носителей заряда (см. Зонная теория ),форма фермы-поверхности, увлечение электронов фононами, тип примесей и т. д. Зависимость коэф. Т. я. от H определяется параметром w_ct где w_c=eH/тс - циклотронная частота носителей запяла (т-их эфф. масса). В случае т. н. слабых магн. полей (w_ct<<1) все коэф. не зависят от H.

Практич. применение Т. я. основано на использовании Пелътье эффекта для охлаждения приборов и устройств, помещённых в сильное магн. поле. Это может приводить к значит. увеличению термоэлектрич. эффективности Z = a²s за счёт роста в магн. поле коэф. термоэдс a при неизменном значении отношения 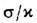(в магн. поле выполняется Видемана - Франца закон).

Литература по термогальваномагнитным явлениям

Цидильковский И. М., Термомагнитные явления в полупроводниках, М., 1960;
Блатт Ф., Физика электронной проводимости в твердых телах, пер, с англ., М.. 1971;
Зеегер К., Физика полупроводников, пер, с англ., М., 1977;
Аскеров Б. М., Электронные явления переноса в полупроводниках, М., 1985;
Гуревич Ю. Г., Парадоксы теплопроводности в полупроводниках, "Природа", 1986, № 3, с. 66.

А. Э. Мейерович

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что, как ни тужатся релятивисты, CMB (космическое микроволновое излучение) - прямое доказательство существования эфира, системы абсолютного отсчета в космосе, и, следовательно, опровержение Пуанкаре-эйнштейновского релятивизма, утверждающего, что все ИСО равноправны, а эфира нет. Это фоновое излучение пространства имеет свою абсолютную систему отсчета, а значит никакого релятивизма быть не может. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира