Эффект Холла. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Эффект Холла - возникновение в твёрдом проводнике с током плотностью j, помещённом в магн. поле Н, элек-трич. поля в направлении, перпендикулярном j и Н. Напряжённость электрич. поля (п о л я Х о л л а)

Здесь a - угол между векторами Н и j (a<180°). Если H | j, то поле Холла Е_Н максимально: E_H = RHj. Коэф. R, наз. постоянной Холла (коэф. Холла), является основной количеств. характеристикой эффекта Холла знак R положителен, если j, Н, Е_H образуют правовинтовую систему координат.

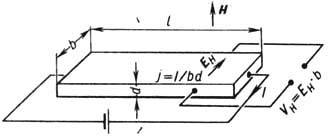
Эффект Холла открыт Э. Г. Холлом (Е. Н. Hall) в 1879 в тонких пластинках Аu. Для наблюдения X. э. прямоуг. пластины из исследуемых веществ длиной l, значительно большей ширины b и толщины d, вдоль к-рых течёт ток I=jbd, помещают в магн. поле Н, перпендикулярное плоскости пластинки (рис.). На середине боковых граней перпендикулярно току расположены электроды, между к-рыми измеряется эдс Холла

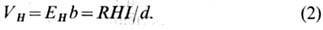
Эффект Холла объясняется взаимодействием носителей заряда (электронов проводимости и дырок) с магн. полем. В магн. поле на электроны действует Лоренца сила:

F=e[Hu](u = =j/пе - ср. скорость направленного движения носителей в электрич. поле, п - концентрация носителей, е - их заряд), под действием к-рой частицы отклоняются в направлении, перпендикулярном j и Н. В результате на боковой грани пластины происходит накопление зарядов и возникает поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. При равновесии eE_H = eHu, откуда

Знак R совпадает со знаком носителей заряда. Для металлов, у к-рых n~10²² см^-3, R~10^-3 см³/Кл, у полупроводников R~10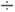10⁵ см³/Кл.

Коэф. Холла может быть выражен через подвижность носителей заряда m = u_др/E (дрейфовая скорость носителей u_др = -eEt/m, где т - эффективная масса ,t - время между двумя последоват. соударениями с рассеивающими центрами) и уд. электропроводность s=j/E=enu_др/E:

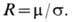
Сказанное справедливо для изотропных проводников, в частности для поликристаллов .Для анизотропных кристаллов R = r/en, где коэф. r - величина, близкая к 1, зависящая от направления Н относительно кристаллографич. осей. В области сильных магн. полей r=1. Критерий сильного поля w_сt>1, где w_с - циклотронная частота носителей.

В полупроводниках в электропроводимости участвуют одновременно электроны проводимости и дырки. При этом постоянная Холла выражается через парциальные проводимости электронов s_э и дырок s_д и их концентрации п_э и n_д. В случае слабых полей

При п_э = п_д для всех значений магнитного поля R = = (1/еn)(s_э-s_д)/(s_э + s_д), а знак R соответствует знаку осн. носителей.

Для металлов величина R зависит от зонной структуры, т. е. формы ферми-поверхности. Для замкнутых поверхностей Ферми и в сильных магн. полях постоянная Холла изотропна, а выражения для R совпадают с (3) и (4). Для открытых поверхностей Ферми R - тензор. Однако если направление Н относительно кристаллографич. осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражения для R также аналогичны (3) и (4).

Эффект Холла - один из наиболее эфф. методов изучения энерге-тич. спектра носителей заряда в металлах и полупроводниках. Зная R, можно определить знак носителей заряда и оценить их концентрацию, что позволяет сделать заключение о кол-ве примесей в полупроводниках. Линейная зависимость R от Н используется для измерения напряжённости магн. поля (см. Магнитометры ),а также для усиления пост. токов, в аналоговых вычислит. машинах, в измерит. технике и др. (Холла датчик).

При изучении Эффекта Холла в двумерном электронном газе кремниевого полевого транзистора, помещённого в квантующее магн. поле, К. фон Клитцинг (К. von Klitzing) в 1980 обнаружил, что холловское сопротивление (R_H=V_H/I), к-рое в условиях обычного X. э., как следует из ф-л (2) и (3), обратно пропорционально п, при изменении п то остаётся постоянным, то резко изменяется, переходя с одного уровня на другой. Вместо монотонного убывания в зависимости R_H(n)наблюдались "ступеньки". При этом высота ступенек определяется такими фундам. константами, как постоянная Планка и заряд электрона, и не зависит от свойств вещества. Это явление получило назв. квантового Холла эффекта. Ю. П. Гайдуков.

При описании Эффекта Холла в магнетиках следует вместо поля Н рассматривать магн. индукцию В=Н+4pМ, где М- намагниченность .Поле Холла в поликристаллич. ферромагнетиках может быть записано в виде

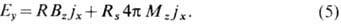
Здесь x, у, z - координатные оси. Первое слагаемое описывает нормальный X. э. Вклад в поле Холла, пропорциональный намагниченности М, наз. ферромагнитным, спонтанным или аномальным эффектом Холла. Т. к. этот вклад существует в ферро-, ферри- и антиферромагн. металлах и полупроводниках, парамагнетиках и др., то термин "аномальный эффект Холла" является наиб. общим. Коэф. R_s в ферромагнетиках на 1-2 порядка больше R и обладает сильной (по сравнению с R)зависимостью от температуры. В сплавах величина и знак R_s зависят от концентрации компонент, причём в общем случае знак R_s может не совпадать со знаком R. В монокристаллах R_s также является тензорной величиной. Роль внеш. магн. поля в создании аномального X. э. сводится только к намагничиванию образца, в частности в однодоменных образцах аномальный эффект Холла наблюдается и без поля.

Аномальный эффект Холла обусловлен спин-орбитальным взаимодействием, к-рое пропорц. намагниченности и создаёт асимметрию рассеяния. носителей заряда, приводящую к холловскому "закручиванию" в отсутствие поля.

Лит. см. при статьях Гальвано магнитные явления, Квантовый Холла эффект. Магнетизм.

Знаете ли Вы, что "гравитационное линзирование" якобы наблюдаемое вблизи далеких галактик (но не в масштабе звезд, где оно должно быть по формулам ОТО!), на самом деле является термическим линзированием, связанным с изменениями плотности эфира от нагрева мириадами звезд. Подробнее читайте в FAQ по эфирной физике.