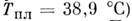 ,
так что в обычных условиях M.- твёрдые тела. При плавлении M. сохраняет металлич.
свойства (см. Жидкие металлы ).Искусственно созданы аморфные твёрдые
M. (см. Аморфные металлы, Металлические стёкла).
,
так что в обычных условиях M.- твёрдые тела. При плавлении M. сохраняет металлич.
свойства (см. Жидкие металлы ).Искусственно созданы аморфные твёрдые
M. (см. Аморфные металлы, Металлические стёкла).Металлы - традиционно определяются как конденсированное состояние вещества (твёрдое тело, жидкость), построенного из
атомов M. в хим. понимании, т. е. легко отдающих электроны в процессе хим. реакций.
Характерные признаки M.: высокие электро- и теплопроводность, причём электропроводность
повышается с понижением темн-ры T, а также пластичность.
Металлическое состояние. Основанием для выделения
M. в отд. класс веществ служит деление всех веществ по электрич. свойствам на
проводники и изоляторы (полупроводники и полуметаллы занимают промежуточное
положение). M.- проводники. Однако нек-рые элементы в зависимости от кристаллич.
структуры могут быть проводниками (M.), изоляторами (диэлектриками), полупроводниками или полуметаллами. Примеры: Sn (белое олово - M., серое - полупроводник);
С (графит - полуметалл, алмаз - диэлектрик, см. Полиморфизм ).В результате
можно говорить о металлич. состоянии вещества, понимая под этим такое состояние,
при к-ром в теле есть достаточно большое кол-во коллективизиров. подвижных электронов
(электронов проводимости или свободных электронов), причём их подвижность не
есть результат термич. возбуждения; если тело в данном состоянии существует
вплоть до T = 0 К, то и при T = 0 К в нём есть электроны проводимости.
Наличие электронов проводимости - обязат. признак структуры M. Представление
о M. как о веществе, состоящем из положит, ионов и свободных электронов, достаточно
точно отражает строение реальных M. Электроны компенсируют силы отталкивания,
действующие между положительно заряженными ионами, и тем самым связывают их
в твёрдое тело или жидкость. Электроны проводимости определяют не только электрич.,
магн., оптич. и др. типично электронные свойства, но и их теплопроводность,
а при низких темп-pax - теплоёмкость. Значительна роль электронов в сжимаемости
M. и др. механич. характеристиках, их наличие делает M. пластичным.
Фазовые переходы в M. сопровождаются изменением
свойств электронной системы. Иногда причиной перехода служит изменение электронного
спектра, а изменение кристаллич. структуры носит вторичный характер [напр.,
переход из нормального состояния M. в сверхпроводящее или из парамагнитного
в ферро-или антиферромагнитное (ФМ, АФМ, табл. 1)], В твёрдом состоянии M.-
кристаллы (в парообразном - одноатомные газы). Темп-ры плавления Tпл
всех M. выше 300 К (кроме Hg с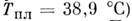 ,
так что в обычных условиях M.- твёрдые тела. При плавлении M. сохраняет металлич.
свойства (см. Жидкие металлы ).Искусственно созданы аморфные твёрдые
M. (см. Аморфные металлы, Металлические стёкла).
,
так что в обычных условиях M.- твёрдые тела. При плавлении M. сохраняет металлич.
свойства (см. Жидкие металлы ).Искусственно созданы аморфные твёрдые
M. (см. Аморфные металлы, Металлические стёкла).
В металлич. состоянии могут находиться сильно
ле-гиров. полупроводники (электроны проводимости в них существуют при T = 0 К), а также вещества, состоящие из неметаллич. атомов, напр, полимерный
кристалл  Металлич.
свойствами обладают нек-рые хим. соединения,
напр, кристаллы окислов типа
Металлич.
свойствами обладают нек-рые хим. соединения,
напр, кристаллы окислов типа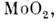
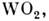 халькогенидов
халькогенидов 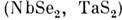 и более сложных соединений (AuTe2,
Br и др., кристаллы, содержащие органич. комплексы, см. Органические проводники), а также многокомпонентные материалы со структурой типа перовскита (напр.,
и более сложных соединений (AuTe2,
Br и др., кристаллы, содержащие органич. комплексы, см. Органические проводники), а также многокомпонентные материалы со структурой типа перовскита (напр.,
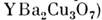 или со слоистой
структурой (напр.,
или со слоистой
структурой (напр.,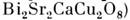 ,
являющиеся высокотемпературными сверхпроводниками
(напр., температура сверхпроводящего перехода
,
являющиеся высокотемпературными сверхпроводниками
(напр., температура сверхпроводящего перехода 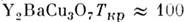 К).
К).
К M. относят интерметаллические соединения типа  ,
AgZn и др., к-рые от обычных M. отличаются лишь более сложной кристаллич. структурой.
,
AgZn и др., к-рые от обычных M. отличаются лишь более сложной кристаллич. структурой.
Большинство M. кристаллизуется в структуры, отвечающие
плотной упаковке атомов с гранецентриров. кубической (ГЦК) и гексагональной
(гекс) решётками (обе имеют макс, координационное число - 12). Др. решётки
M. тоже достаточно просты: объёмноцентри-рованная кубическая (ОЦК) у щелочных
M., тетрагональная (тетр) с 1-2 атомами в элементарной ячейке. Лишь небольшое
число M. имеют более сложное строение (слож.), напр. Mn, в элементарной ячейке
к-рого 58 атомов (табл. 1).
За исключением Au, Ag, Pt, Cu, встречающихся
в самородном состоянии, остальные M. в природе существуют в составе хим. соединений
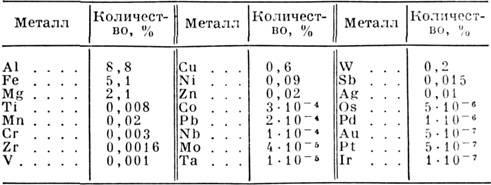
- окислов, сульфидов и др., образующих руды. Относит, распространённость нек-рых
M. в земной коре приведена в табл. 2.
Табл. 2.
Промышл. использование M. прямо не связано с
их распространённостью в земной коре, а зависит от развития способов извлечения
M. из руд, очистки, потребностей техники и т. п. Широкое применение самого распространённого
на Земле M.- Al началось лишь в 20 в. По-видимому, первый M., использованный
человеком,- Cu.
Обычно анизотропия свойств M., напр, анизотропия
электропроводности ,
выражена слабо. Однако в ряде случаев особенности структуры, напр, слоистое
строение графита, графита, интеркалированного примесями (см. Интеркалированные
соединения), дихалькогени-дов, приводят к различию s вдоль и поперёк
слоев на неск. порядков. В комплексных соединениях, обладающих металлич. свойствами,
таких, как
,
выражена слабо. Однако в ряде случаев особенности структуры, напр, слоистое
строение графита, графита, интеркалированного примесями (см. Интеркалированные
соединения), дихалькогени-дов, приводят к различию s вдоль и поперёк
слоев на неск. порядков. В комплексных соединениях, обладающих металлич. свойствами,
таких, как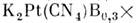
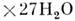 , или в соединениях, молекулы к-рых содержат комплекс тетрацианохинодиметана
(TCNQ), проводимость осуществляется по цепочкам металлич. атомов. Вдоль
этих цепочек она на много порядков выше, чем проводимость в поперечном направлении
(см. Квазиодномерные соединения). Двумерные M. создаются искусственно,
напр, в тонких плёнках (см. Квазидвумерные соединения).
, или в соединениях, молекулы к-рых содержат комплекс тетрацианохинодиметана
(TCNQ), проводимость осуществляется по цепочкам металлич. атомов. Вдоль
этих цепочек она на много порядков выше, чем проводимость в поперечном направлении
(см. Квазиодномерные соединения). Двумерные M. создаются искусственно,
напр, в тонких плёнках (см. Квазидвумерные соединения).
Число электронов проводимости в 1 см3
(или их число на элементарную ячейку кристалла либо на 1 атом) h -
важнейшая характеристика металлич. состояния. Как правило, из всех атомарных
электронов "освобождаются" (коллективизируются) только валентные.
Это даёт возможность по хим. свойствам атомов, из к-рых состоит кристалл, и
по его геом. структуре определить h как 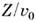 ,
где Z - число валентных электронов в элементарной ячейке объёма v0
(табл. 3).
,
где Z - число валентных электронов в элементарной ячейке объёма v0
(табл. 3).
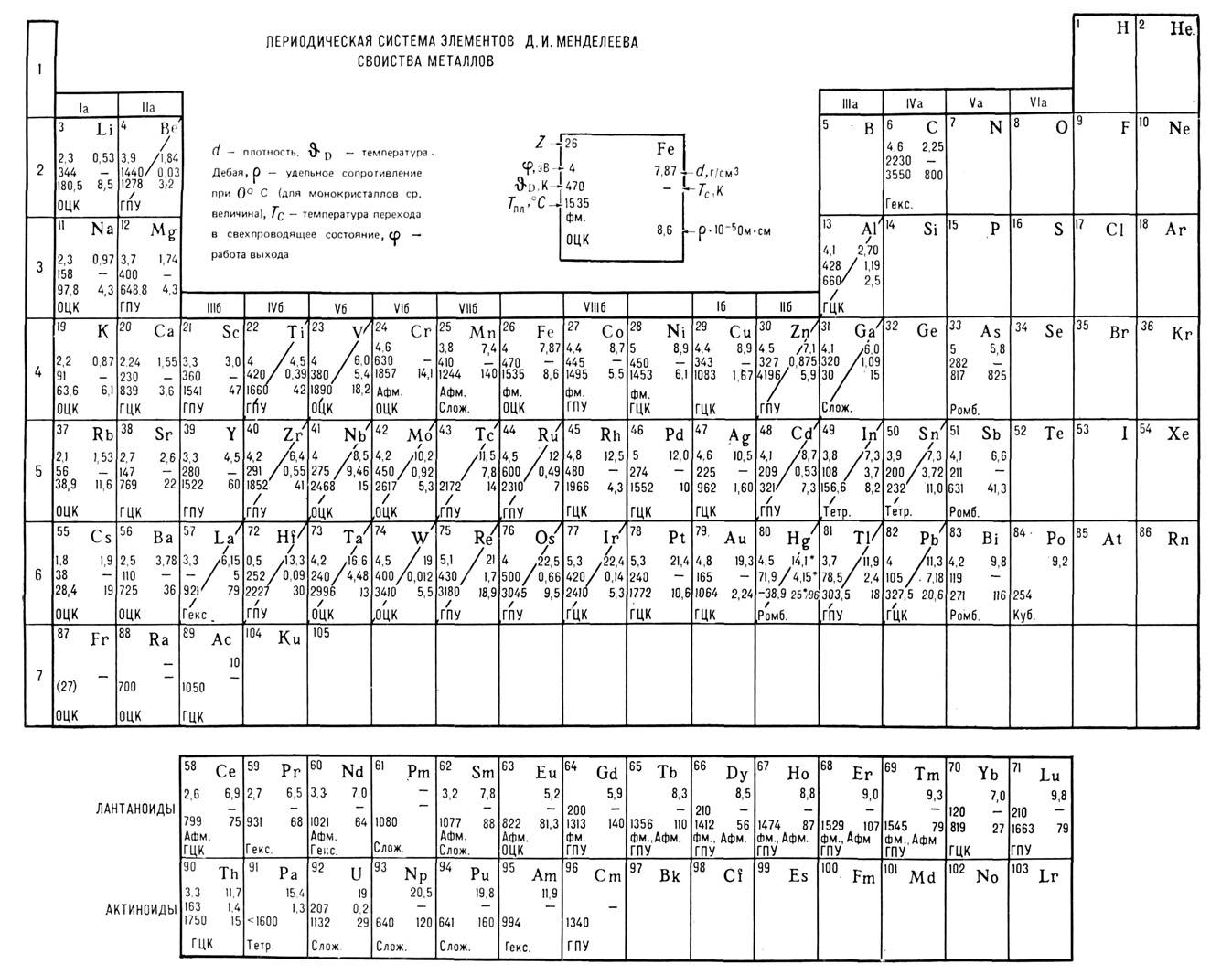
Табл. 3. Плотность электронов проводимости
h и энергия Ферми 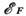 ряда металлов
ряда металлов

Природа металлического состояния. MH. характерные
свойства M. можно понять, считая, что электроны проводимости - идеальный вырожденный
газ фермионое ,а роль ионов сводится к созданию потенциальной ямы, в
к-рой движутся электроны (модель Друде - Лоренца - Зоммерфельда; см. Друде
теория металлов, Зом-мерфельда теория металлов). Темп-pa вырождения Tp электронного газа в этой модели определяется энергией Ферми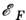
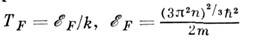 :
:
(т - масса электрона). Тсмп-ра 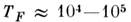 К.
К.
Поэтому практически при любой температуре T, при
к-рой вещество существует в конденсиров. состоянии, электронный газ в M. вырожден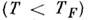 (см.
Вырождения температура, Вырожденный газ).
(см.
Вырождения температура, Вырожденный газ).
Более полное и строгое объяснение свойств M.
даёт зонная теория твёрдого тела. Зонная теория исходит из рассмотрения
движения отд. электрона в периодич. поле сил 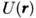 ,
создаваемых ионами кристаллич. решётки и
остальными электронами (одноэлектронное приближение):
,
создаваемых ионами кристаллич. решётки и
остальными электронами (одноэлектронное приближение):
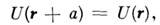
где r - пространств, координата
точки, a - период решётки (см. Блоховские электроны ).Хотя энергия
взаимодействия электронов друг с другом не меньше, чем энергия взаимодействия
с ионами, одноэлектронное приближение имеет обоснование. Во-первых, 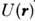 включает совокупное действие всех остальных
электронов, кроме рассматриваемого, причём для качеств, выводов потенциал U(r)можно не конкретизировать, используя только его свойства симметрии (прежде
всего периодичность). Во-вторых, построив одноэлектронное приближение, можно
обобщить его, учтя взаимодействие между электронами проводимости (на основании
теории ферма-жидкости).
включает совокупное действие всех остальных
электронов, кроме рассматриваемого, причём для качеств, выводов потенциал U(r)можно не конкретизировать, используя только его свойства симметрии (прежде
всего периодичность). Во-вторых, построив одноэлектронное приближение, можно
обобщить его, учтя взаимодействие между электронами проводимости (на основании
теории ферма-жидкости).
Периодичность U(r)позволяет характеризовать
стационарное состояние электрона проводимости квазиимпульсом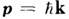 (
(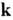 -
квазиволновой вектор), аналогичным импульсу частицы в свободном пространстве.
Волновая функция электрона в стационарном состоянии - решение Шрёдингера уравнения для электрона, отвечающая собств. значению энергии электрона
-
квазиволновой вектор), аналогичным импульсу частицы в свободном пространстве.
Волновая функция электрона в стационарном состоянии - решение Шрёдингера уравнения для электрона, отвечающая собств. значению энергии электрона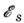 .
И волновая функция и собств. значение энергии (в отличие от случая свободного
электрона) - периодич. функции квазиимпульса. Периодичность в импульсном пространстве
- следствие полной физ. эквивалентности состояний с квазиволновыми векторами,
отличающимися на
.
И волновая функция и собств. значение энергии (в отличие от случая свободного
электрона) - периодич. функции квазиимпульса. Периодичность в импульсном пространстве
- следствие полной физ. эквивалентности состояний с квазиволновыми векторами,
отличающимися на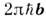 .
Это означает, что для полного описания всех состояний достаточно использовать
.
Это означает, что для полного описания всех состояний достаточно использовать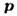 из
одной ячейки обратного пространства. Как правило, её выбирают в виде первой
Бриллюэна зоны. Индекс s, нумерующий решения ур-ния Шрёдингера, наз.
номером зоны,
из
одной ячейки обратного пространства. Как правило, её выбирают в виде первой
Бриллюэна зоны. Индекс s, нумерующий решения ур-ния Шрёдингера, наз.
номером зоны, 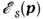 - законом дисперсии электронов или электронным спектром кристалла, соответствующим
полю
- законом дисперсии электронов или электронным спектром кристалла, соответствующим
полю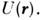 В каждой
разрешённой эноргетич. зоне состояния электронов заполняют полосу между
В каждой
разрешённой эноргетич. зоне состояния электронов заполняют полосу между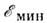 и
и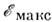 .
Зоны могут перекрываться, но их индивидуальность при этом сохраняется. Перекрытие
зон, как правило, не сопровождается вырождением. Вырождение наступает при совпадении
энергий (из разных зон) и квазиимпульсов. Вырождение накладывает ограничение
на структуру изоэнергетич. поверхности вблизи точки вырождения. С помощью законов
дисперсии можно рассчитать плотность электронных состоянии в зоне
.
Зоны могут перекрываться, но их индивидуальность при этом сохраняется. Перекрытие
зон, как правило, не сопровождается вырождением. Вырождение наступает при совпадении
энергий (из разных зон) и квазиимпульсов. Вырождение накладывает ограничение
на структуру изоэнергетич. поверхности вблизи точки вырождения. С помощью законов
дисперсии можно рассчитать плотность электронных состоянии в зоне 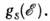
Сходство и различие между свободными электронами
и электронами проводимости иллюстрируется табл. 4.
Табл. 4.

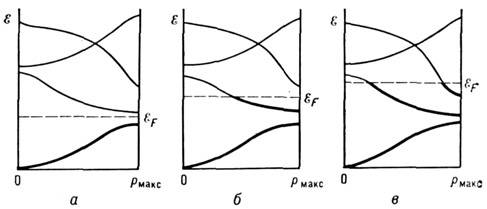
Рис. 1. Схема заполнения зон диэлектрика или
полупроводника (а), металла (б), полуметалла (в). Жирные линии /(P)-
заполненные состояния, тонкие - пустые; пунктир - уровень химического потенциала,
совпадающий в металлах с энергией Ферми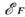 при
при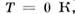
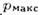 - максимальный
квазиимпульс, соответствующий границе зоны
Бриллюэна.
- максимальный
квазиимпульс, соответствующий границе зоны
Бриллюэна.
Зонный характер спектра и Паули принцип позволяют сформулировать принципиальное
отличие M. от диэлектрика. T. к. в каждую зону может «поместиться» не более
2N электронов (N - число ячеек в кристалле), то в зависимости от числа электронов,
приходящихся на ячейку, и взаимного расположения зон могут осуществляться
2 случая: либо в осн. состоянии (при T = 0 K) имеются только целиком
заполненные зоны и пустые (рис. 1, а), либо есть зоны, частично заполненные
электронами (рис. 1, б, в). В первом случае кристалл - диэлектрик
(или полупроводник), во втором - M. (рис. 1, в соответствует полуметаллу).
Поверхность Ферми. В M. граница заполнения уровней
электронами попадает в разрешённую зону и наз. энергией Ферми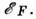 Соответствующая
ей изоэнергетич. поверхность
Соответствующая
ей изоэнергетич. поверхность
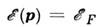
наз. поверхностью Ферми. Поверхность Ферми отделяет
область занятых электронами состояний в импульсном пространстве от свободных.
Поверхность Ферми - обязат. атрибут металлич.
состояния кристаллов. Если поверхность Ферми пересекает границы зоны Бриллюэна
(напр., у Cu), то удобно использовать расширенное 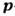 -пространство.
В этом случае отчётливо видна его периодичность. У щелочных металлов (Li, Na,
К, Pb, Cs) поверхности Ферми - почти идеальные сферы. Это не означает, что электроны
этих металлов не испытывают влияния ионов. Их эффективные массы
-пространство.
В этом случае отчётливо видна его периодичность. У щелочных металлов (Li, Na,
К, Pb, Cs) поверхности Ферми - почти идеальные сферы. Это не означает, что электроны
этих металлов не испытывают влияния ионов. Их эффективные массы 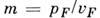 отличаются
от массы свободного электрона т0 (табл. 4), напр, у
отличаются
от массы свободного электрона т0 (табл. 4), напр, у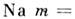
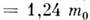 . У всех M., кроме перечисленных, а также у Au, Ag, Cu поверхности Ферми состоят
из неск. полостей-листов и имеют сложную форму (рис. 2).
. У всех M., кроме перечисленных, а также у Au, Ag, Cu поверхности Ферми состоят
из неск. полостей-листов и имеют сложную форму (рис. 2).
Из-за столкновений электронов с дефектами решётки,
друг с другом, а также с фононами состояние электрона проводимости имеет конечное
время жизни 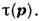 Это
означает, что мнимая часть функции
Это
означает, что мнимая часть функции 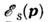 отлична от 0:
отлична от 0: 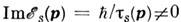 . Это не лишает поверхность
. Это не лишает поверхность
a
Рис. 2. Поверхности Ферми W (ОЦК, a), Gd (гексагональная
решётка, б).
Ферми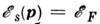 строго определённого смысла, т. к.
строго определённого смысла, т. к. 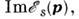 обязанная неупругим столкновениям (электронов с фононами или друг о другом),
для электронов на поверхности Ферми равна О. Упругие столкновения со статич.
дефектами приводят к "перемещению" электронов по поверхности Ферми.
Если время жизни (т) электрона мало (много дефектов, высокая темп-pa),
то строгое описание его движения с помощью закона дисперсии теряет смысл. При
этом лишается смысла и т. н. тонкая структура поверхности Ферми (отклонение
от сферичности), хотя подвижность электрона сохраняется - электроны проводимости
остаются делокализован-ными (их длина пробега существенно превышает межатомное
расстояние). Приближённое описание электронов в таких условиях возможно лишь
с помощью модели Друде - Лоренца - Зоммерфельда.
обязанная неупругим столкновениям (электронов с фононами или друг о другом),
для электронов на поверхности Ферми равна О. Упругие столкновения со статич.
дефектами приводят к "перемещению" электронов по поверхности Ферми.
Если время жизни (т) электрона мало (много дефектов, высокая темп-pa),
то строгое описание его движения с помощью закона дисперсии теряет смысл. При
этом лишается смысла и т. н. тонкая структура поверхности Ферми (отклонение
от сферичности), хотя подвижность электрона сохраняется - электроны проводимости
остаются делокализован-ными (их длина пробега существенно превышает межатомное
расстояние). Приближённое описание электронов в таких условиях возможно лишь
с помощью модели Друде - Лоренца - Зоммерфельда.
Нек-рые свойства M. (гл. обр. в сильном магн.
поле) очень чувствительны к форме поверхности Ферми (де Хааза - вот
Альфена эффект, Циклотронный резонанс, геом. резонанс и др.). Они позволили
восстановить поверхность Ферми практически
для всех моноатомных M. и MH. интерметаллич. соединений (AuAl2, AuGa2,
CuZn, AuTe2I и др.). а также в большом числе случаев определить скорости
фермиевских электронов Vp (щелочные, благородные M., Bi, Sb и др.).
Методы зонной теории (с использованием ЭВМ) позволили
определить законы дисперсии с большой точностью. Все вычислит, методы основаны
на приближении почти свободных электронов (модель Гаррисона, или метод псевдопотенциала)
и (или) на т. н. приближении сильной связи. Они дают возможность выяснить происхождение
отд. характерных деталей электронного спектра M.: наличие или отсутствие тех
или др. листов поверхности Ферми, величину и зависимость плотности состояний
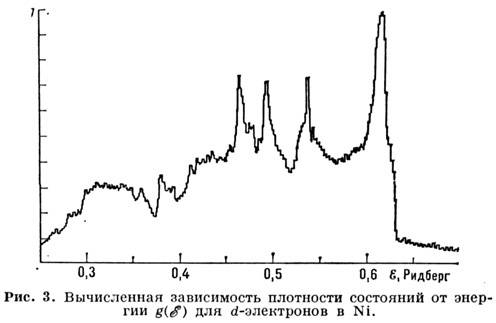
от энергии 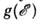 (рис. 3); значение скоростей электронов,
а также величину эфф. потенциала (или псевдопотенциала), определяющего электронный
энергетич. спектр конкретного M.
(рис. 3); значение скоростей электронов,
а также величину эфф. потенциала (или псевдопотенциала), определяющего электронный
энергетич. спектр конкретного M.
При всей сложности законов дисперсии представление
об электронах M. как лёгких (по сравнению с ионами) заряженных частицах качественно
правильно. Оно, возвращая нас к модели Друде - Лоренца - Зоммер-фельда, даёт
возможность оценивать порядок величины осн. характеристик M.- электронную теплоёмкость,
эл.- и теплопроводность, толщину скин-слоя (см. Скин-эффект)и т.
д. Правда, нек-рые соединения (CeAl3, CeCu6, CeCu2Si2,
UB13 и др.) обнаруживают необычные свойства (напр., гигантскую электронную
теплоёмкость), заставляющие сделать вывод, что в них есть электроны, обладающие
аномально большой эфф. массой т Эти
электроны получили назв. тяжёлых фермионов.
Эти
электроны получили назв. тяжёлых фермионов.
При все
электроны проводимости находятся на и внутри
поверхности Ферми. Элементарные возбуждения электронной подсистемы M.- электроны
с энергией
все
электроны проводимости находятся на и внутри
поверхности Ферми. Элементарные возбуждения электронной подсистемы M.- электроны
с энергией и
дырки - свободные состояния с энергией
и
дырки - свободные состояния с энергией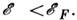 T.
к. обычно
T.
к. обычно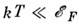 ,то
осн. роль в процессах переноса играют электроны
и дырки с энергиями
,то
осн. роль в процессах переноса играют электроны
и дырки с энергиями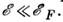 Их
закон дисперсии можно считать линейным:
Их
закон дисперсии можно считать линейным:
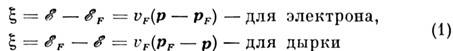
(up - скорость на поверхности Ферми).
Энергию электрона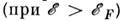 и
дырки принято отсчитывать от
и
дырки принято отсчитывать от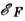 (скорость дырки -
(скорость дырки -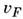 ).
Спектр электронов и дырок демонстрирует наличие разрешённых значений энергии
над поверхностью Ферми (рис. 4, а).
).
Спектр электронов и дырок демонстрирует наличие разрешённых значений энергии
над поверхностью Ферми (рис. 4, а).
При фазовом переходе электронный спектр M. (в
частности, поверхность Ферми) изменяется. Если это переход 1-го рода, то новая
поверхность не связана со старой. Если же это переход 2-го рода, то обе поверхности
Ферми в момент перехода совпадают и можно проследить, как трансформируется поверхность.
На рис. 5 показано снятие вырождения по
спину и изменение поверхности Ферми при переходе M. из парамагн. состояния в
ферромагнитное (поверхность Ферми - сфера). При переходе M. в сверхпроводящее
состояние в спектре электронов возникает щель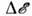 -
область запрещённых значений энергии (рис. 4, б), к-рая обеспечивает
недиссипативный характер сверхпроводящего тока (см. Сверхпроводимость ).Внеш.
воздействие на M. (напр., давление) может привести к изменению связности поверхности
Ферми: либо образуется новый лист, либо рвётся перемычка между листами. Это
сопровождается аномалиями электронных характеристик. При
-
область запрещённых значений энергии (рис. 4, б), к-рая обеспечивает
недиссипативный характер сверхпроводящего тока (см. Сверхпроводимость ).Внеш.
воздействие на M. (напр., давление) может привести к изменению связности поверхности
Ферми: либо образуется новый лист, либо рвётся перемычка между листами. Это
сопровождается аномалиями электронных характеристик. При  такой переход следует считать фазовым переходом
такой переход следует считать фазовым переходом  -го рода (см. Ван Хова особенности). Нек-рые фазовые переходы в M. связаны
с межэлектронными взаимодействиями, к-рые приводят к возникновению волн зарядовой
плотности или волн спиновой плотности, а также к вигнеровской кристаллизации.
-го рода (см. Ван Хова особенности). Нек-рые фазовые переходы в M. связаны
с межэлектронными взаимодействиями, к-рые приводят к возникновению волн зарядовой
плотности или волн спиновой плотности, а также к вигнеровской кристаллизации.
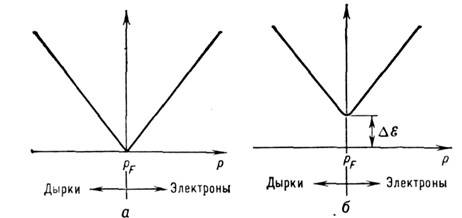
Рис. 4. Спектр электронных возбуждений a
- в нормальном металле; б - в сверхпроводнике.
a
- в нормальном металле; б - в сверхпроводнике.
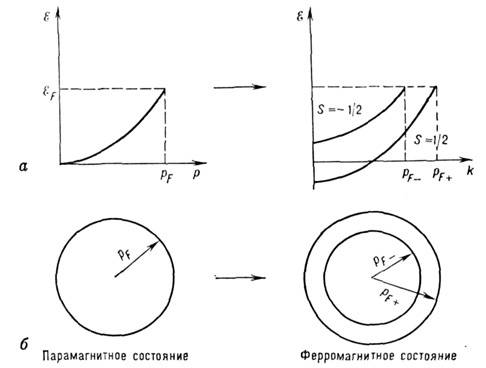
Рис. 5. Изменение спектра электронов (а) и трансформация
поверхности Ферми (б) при переходе металла в ферромагнитное состояние.
Исследования поверхности твёрдых тел привели
к понятию двумерного электронного газа - искусств, двумерного M., обладающего
рядом особенностей; напр., поверхность Ферми двумерного M.- линия, и все особенности,
обусловленные её изменением в двумерном M., выражены отчётливее, чем в трёхмерном.
При достаточно высоких давлениях, когда объём,
приходящийся на 1 атом, становится меньше обычных атомных размеров, атомы теряют
свою индивидуальность и любое вещество превращается в сильно сжатую электронно-ядерную
плазму, т. е. в своеобразный M. Металлизация любого вещества происходит при
плотности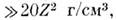 где
Z - ат. номер вещества. При таких плотностях большинство свойств вещества
определяется вырожденным электронным газом.
где
Z - ат. номер вещества. При таких плотностях большинство свойств вещества
определяется вырожденным электронным газом.
Электрические свойства. Характерное свойство
M. как проводников электрич. тока в нормальном (несверхпроводящем)
состоянии - линейная зависимость между плотностью тока j и напряжённостью
приложенного эле-ктрич. поля E (Ома закон):
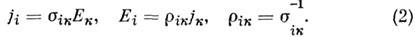
Тензор уд. электропроводности sik
(или тензор сопротивления rik)
- важнейшая характеристика M. Число независимых компонент тензора sik
(или rik),
а значит и тип анизотропии сопротивления, зависит от симметрии кристалла. Для кубич. кристаллов и нетекстуриров. поликристаллов тензор превращается
в скаляр (табл.2).
Носители заряда в M.- электроны проводимости
с энергией, близкой к Причиной
сопротивления служит рассеяние электронов на любых нарушениях периодичности
кристаллич. решётки. Это тепловые колебания ионов (фононы), сами электроны (см.
Межэлектронное рассеяние ),а также разл. дефекты - примесные атомы, вакансии
(сечение рассеяния 10-16-10-15 см-2), дислокации, (сечение 10-8-10-7 см-1), границы кристаллов
и образца (см. Рассеяние носителей заряда).
Причиной
сопротивления служит рассеяние электронов на любых нарушениях периодичности
кристаллич. решётки. Это тепловые колебания ионов (фононы), сами электроны (см.
Межэлектронное рассеяние ),а также разл. дефекты - примесные атомы, вакансии
(сечение рассеяния 10-16-10-15 см-2), дислокации, (сечение 10-8-10-7 см-1), границы кристаллов
и образца (см. Рассеяние носителей заряда).
Мерой проводимости служит длина свободного пробега (l) электронов:

где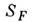 -
площадь поверхности Ферми. Для сферич. поверхности Ферми
-
площадь поверхности Ферми. Для сферич. поверхности Ферми
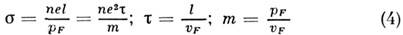
(vF - скорость фермиевских
электронов). При T = 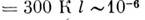 см, с понижением T пробег l растёт, достигая (для специально очищенных
образцов) 0,1-1 см. Соответственно возрастает проводимость. Отношение проводимости
при T = 0K (s0) к проводимости при 300 К (s300)
характеризует совершенство и хим. чистоту M. Достигнутые значения
см, с понижением T пробег l растёт, достигая (для специально очищенных
образцов) 0,1-1 см. Соответственно возрастает проводимость. Отношение проводимости
при T = 0K (s0) к проводимости при 300 К (s300)
характеризует совершенство и хим. чистоту M. Достигнутые значения 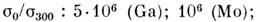
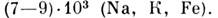
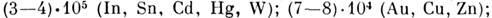
Отсутствие корреляции между разл. механизмами
рассеяния приводит к приближённому соотношению 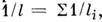 где
где 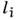 - длина
свободного пробега относительно определённого механизма рассеяния. Этим объясняется
эмпирич. Маттиссена правило ,согласно к-рому сопротивление конкретного
образца M. есть сумма остаточного сопротивления р0, обусловленного
рассеянием на дефектах решётки (совпадает с r при T = 0 K), и сопротивления
идеального кристалла РИД, обязанного рассеянию на фононах и др. квазичастицах.
Гл. причина температурной зависимости - рассеяние электронов на фононах. При
- длина
свободного пробега относительно определённого механизма рассеяния. Этим объясняется
эмпирич. Маттиссена правило ,согласно к-рому сопротивление конкретного
образца M. есть сумма остаточного сопротивления р0, обусловленного
рассеянием на дефектах решётки (совпадает с r при T = 0 K), и сопротивления
идеального кристалла РИД, обязанного рассеянию на фононах и др. квазичастицах.
Гл. причина температурной зависимости - рассеяние электронов на фононах. При
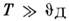
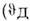 -
Девая температура)
-
Девая температура)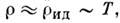 причём
типичное значение
причём
типичное значение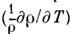 при
T = 300 К равно
при
T = 300 К равно 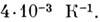 При
При 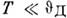 фононная часть быстро стремится к О, что позволяет в ряде случаев выделить в
зависимости rид(Т)вклад рассеяния на электронах, к-рый пропорц,
фононная часть быстро стремится к О, что позволяет в ряде случаев выделить в
зависимости rид(Т)вклад рассеяния на электронах, к-рый пропорц, 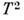 (рис.
6).
(рис.
6).
Сопротивление сплавов и M. типа керамик значительно
выше, чем у чистых M. Причина этого в нарушении идеальности решётки (разл. атомы
в узлах решётки) и в её дефектности. Предельное уд. сопротивление M., достигаемое
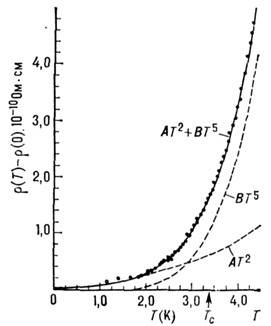
при Рис. в. Зависимость удельного сопротивления
r от T. Точки - измеренные значения за вычетом остаточного сопротивления
8,8*10-10 Ом*см;
сплошная линия - зависимость вида АТ 2 + BT 5,
представляет сумму электрон-электронного и электрон-фононного вкладов.
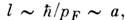 равно
равно 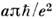 (в трёхмерном
случае) и
(в трёхмерном
случае) и 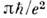 (в двумерном). В веществах с большим r возникает локализация электронных
состояний - проводимость исчезает (см. Андерсоновская локализация ).При
этом исчезновение проводимости происходит не за счёт "связывания"
электронов ионами - электроны остаются коллективизированными (в том смысле,
что их волновая функция "размазана" на расстояния, много большие атомных).
(в двумерном). В веществах с большим r возникает локализация электронных
состояний - проводимость исчезает (см. Андерсоновская локализация ).При
этом исчезновение проводимости происходит не за счёт "связывания"
электронов ионами - электроны остаются коллективизированными (в том смысле,
что их волновая функция "размазана" на расстояния, много большие атомных).
При плавлении подвижные электроны в M. сохраняются,
поэтому сохраняется большая электропроводность, хотя разрушение дальнего порядка
приводит к скачкообразному росту r (табл. 5; см. также Жидкие металлы). Исключение составляют Sb, Ga, Bi, у к-рых при плавлении r уменьшается
(для этих M. плавление сопровождается увеличением плотности).
Табл. 5.- Отношение удельных сопротивлений
в твёрдой (rт)
и жидкой (rж)
фазах при температуре плавления

Большинство M. при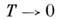 К
теряют сопротивление - переходят в сверхпроводящее
состояние. Для таких M. зависимость r(Т)при
К
теряют сопротивление - переходят в сверхпроводящее
состояние. Для таких M. зависимость r(Т)при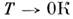 определяют,
разрушив сверхпроводящее состояние магн.
полем
определяют,
разрушив сверхпроводящее состояние магн.
полем 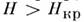 (см.
Сверхпроводимость).
(см.
Сверхпроводимость).
Теплоёмкость. Существование в M. вырожденного
электронного газа большой плотности приводит к линейной зависимости теплоёмкости
M. от Г при низкой температуре (рис. 7). Вклад электронов в теплоёмкость M.
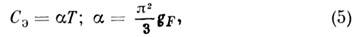
где gF - суммарная (по всем
частично заполненным зонам) плотность электронных состояний при 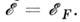 Измерение Cэ - один из осн. методов определения
Измерение Cэ - один из осн. методов определения 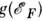 (табл. 6).
(табл. 6).
Рис. 7. Низкотемпературная теплоёмкость нормального
(Сн) и сверхпроводящего (Ссв) Al (при T
< Tc значения Сн измерены на образцах, в
которых сверхпроводимость была разрушена магнитным полем).
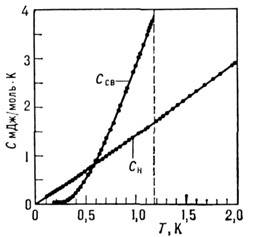
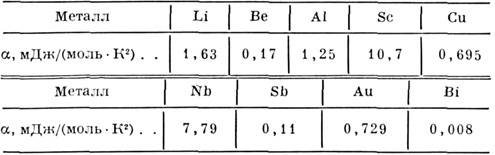
Табл. 6. - Значения постоянной а, определённые
по электронной теплоёмкости C3
Электроны проводимости вносят линейный по T вклад не только в теплоёмкость M., но и в его коэф. теплового расширения.
Из-за этого в M. нарушается Грюнайзена закон: при низких температурах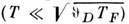 константа в законе Грюнайзена определяется электронной подсистемой, а при высоких
константа в законе Грюнайзена определяется электронной подсистемой, а при высоких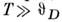 -
фононной (колебаниями решетки).
-
фононной (колебаниями решетки).
Теплопроводность, термоэлектрические явления.
Электроны проводимости принимают участие не только в переносе электрич. заряда,
но и в переносе тепла. Вследствие большой подвижности электронов теплопроводность
M. велика. Величины электропроводности и электронной
части теплопроводности M. l связаны соотношением (Видемана - Франца
закон):

Оно выполняется тем лучше, чем строже столкновения
электронов можно считать упругими (при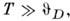 а также и при T = 0 K, когда
осн. причина сопротивления - столкновения с дефектами кристалла). При наличии
градиента температуры
а также и при T = 0 K, когда
осн. причина сопротивления - столкновения с дефектами кристалла). При наличии
градиента температуры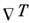 в M. возникает электрич. ток, или связанная с
в M. возникает электрич. ток, или связанная с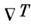 разность потенциалов (термоэдс ).Из-за вырождения электронного газа коэф.,
описывающие термоэдс и др. термоэлектрич. эффекты, малы, однако их исследование
позволяет обнаружить увлечение электронов тепловыми фононами. Взаимодействия
внеш. возбуждённых в M. акустич. волн с электронами проводимости приводят к
возникновению тока либо разности потенциалов, пропорц. интенсивности потока
фононов (см. Акустоэлектрический эффект ).Теплопроводность сплавов ниже
теплопроводности чистых M.
разность потенциалов (термоэдс ).Из-за вырождения электронного газа коэф.,
описывающие термоэдс и др. термоэлектрич. эффекты, малы, однако их исследование
позволяет обнаружить увлечение электронов тепловыми фононами. Взаимодействия
внеш. возбуждённых в M. акустич. волн с электронами проводимости приводят к
возникновению тока либо разности потенциалов, пропорц. интенсивности потока
фононов (см. Акустоэлектрический эффект ).Теплопроводность сплавов ниже
теплопроводности чистых M.
Диамагнетизм и парамагнетизм M. Электроны проводимости
обладают как парамагнитными (из-за наличия у каждого электрона собств. магн.
момента), так и диамат, свойствами, обязанными квантованию движения электронов
в плоскости, перпендикулярной магн. полю (см. Диамагнетизм ).В теории
Друде - Лоренца - Зоммерфельда (с эфф. массой т электрона вместо т0)
магнитная восприимчивость электронного газа равна:
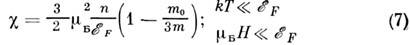
(mБ - магнетон Бора).
Из ф-лы (3) видно, что электронный газ в зависимости от соотношения между т и та может быть как диамагнитным, так и парамагнитным.
Более строгое рассмотрение не изменяет этого вывода и оценки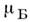 по
порядку величины, табл. 7.
по
порядку величины, табл. 7.
Табл. 7.- Магнитная восприимчивость c
поликристаллических металлов при T = 300 К

В магн. восприимчивость M. вносят вклад и ионы:
у непереходных M. ионы диамагнитны, а у переходных, как правило, парамагнитны
(см. Магнетизм ).Из-за вырождения электронного газа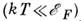 парамагн.
восприимчивость электронного газа слабо
зависит от T (см. Паули парамагнетизм ).В сильном магн. поле
парамагн.
восприимчивость электронного газа слабо
зависит от T (см. Паули парамагнетизм ).В сильном магн. поле 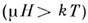
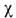 металлич. монокристаллов осциллирует как функция 1/H с частотами, пропорц.
площадям экстремальных сечений поверхности Ферми (эффект де Хааза - ван Альфена,
см. Квантовые осцилляции в магнитном поле).
металлич. монокристаллов осциллирует как функция 1/H с частотами, пропорц.
площадям экстремальных сечений поверхности Ферми (эффект де Хааза - ван Альфена,
см. Квантовые осцилляции в магнитном поле).
Нек-рые M. при понижении T переходят в
магнито-упорядоченное состояние: в ферромагнитное (напр., Fe, Со, Ni), в антиферромагнитное
(Ce, Mn) или в состояние с геликоидальной магнитной атомной структурой (напр.,
Cr, табл. 1). При этом электроны проводимости играют существ, роль в формировании
магн. структур (см. Ферромагнетизм, Антиферромагнетизм). Упорядочение
магн. моментов при понижении температуры - необязат. свойство осн. состояния M.;
большинство непереходных металлов остаются парамагнетиками или диамагнетиками
вплоть до T = 0 K.
Переход кристаллич. M. в сверхпроводящее состояние
сопровождается изменением его магн. свойств: в сверхпроводящем состоянии M.
в слабых нолях проявляет себя как диамагнетик. Из-за Мейснера эффекта ср.
значение магн. поля в сверхпроводнике равно 0. В сверхпроводниках 1-го рода
(Sn, Pb, In и др.) это выполняется вплоть
до полей, разрушающих сверхпроводимость. В сверхпроводниках 2-го рода (Nb3Sn,
NbTi и др.) в широком диапазоне H поле, не разрушая сверхпроводимости,
проникает в объём в виде вихрей, что эффективно ослабляет диамагнетизм.
Эмиссия электронов. При нагревании M. до высоких
температур наблюдается "испарение" электронов с поверхности M. (см.
Термоэлектронная эмиссия ).Число электронов, вылетающих из M. в единицу
времени, пропорц. ехр (-W/kT), где W - работа выхода электрона
из M. Величина W (2-5 эВ) у разл. M. (и даже на разных кристаллич. гранях
одного M.) различна; W зависит от состояния поверхности. Приложив к M.
сильное электрич. поле (~107 В/см), можно существенно увеличить эмиссию
электронов за счёт того, что электроны покидают M. в результате туннельного
прохождения (см. Автоэлектронная эмиссия ).Различия в W обусловливают
контактную разность потенциалов между разными M.
Гальваномагнитные и термомагнитные явления. Магн.
поле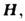 искривляя
траекторию электронов в плоскости, перпендикулярной
искривляя
траекторию электронов в плоскости, перпендикулярной 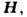 влияет на все кинетич. коэф. (эл.- и теплопроводностей, термоэлектрические и
др.) и приводит к ряду новых явлений: к Холла эффекту, маг-нетосопротивлению и др. Различают классич. и квантовые (осцилляционные) гальванотермомагнитные
явления. При рассмотрении последних надо учитывать квантование движения электронов
проводимости в плоскости, перпендикулярной
влияет на все кинетич. коэф. (эл.- и теплопроводностей, термоэлектрические и
др.) и приводит к ряду новых явлений: к Холла эффекту, маг-нетосопротивлению и др. Различают классич. и квантовые (осцилляционные) гальванотермомагнитные
явления. При рассмотрении последних надо учитывать квантование движения электронов
проводимости в плоскости, перпендикулярной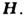 Для
оценки классич. эффектов надо сравнивать ср. радиус орбиты электрона в магн.
поле
Для
оценки классич. эффектов надо сравнивать ср. радиус орбиты электрона в магн.
поле 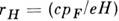 с длиной
пробега l, а для оценки квантовых
- расстояние между уровнями энергии
с длиной
пробега l, а для оценки квантовых
- расстояние между уровнями энергии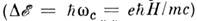 с kT
с kT 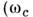 -
циклотронная частота, т - эфф. масса в магн. поле; табл. 4). На зависимость
кинетич. коэф. от
-
циклотронная частота, т - эфф. масса в магн. поле; табл. 4). На зависимость
кинетич. коэф. от 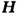 влияют особенности электронного энергетич. спектра M., в частности то, какой
формой (топологией) обладает поверхность Ферми (см. Галъвано.чагнитные явления,
Термогалъваномаг-нитные явления). Даже не слишком большое магн. поле при
низких темп-pax (~1 К) может изменить кинетич. свойства M., напр, в десятки
тысяч раз увеличить поперечное (относительно H)сопротивление (Bi) или
практически полностью "выключить" поперечную электронную теплопроводность
M. (таким путём "выделяют" решёточную- фононную часть теплопроводности
M.).
влияют особенности электронного энергетич. спектра M., в частности то, какой
формой (топологией) обладает поверхность Ферми (см. Галъвано.чагнитные явления,
Термогалъваномаг-нитные явления). Даже не слишком большое магн. поле при
низких темп-pax (~1 К) может изменить кинетич. свойства M., напр, в десятки
тысяч раз увеличить поперечное (относительно H)сопротивление (Bi) или
практически полностью "выключить" поперечную электронную теплопроводность
M. (таким путём "выделяют" решёточную- фононную часть теплопроводности
M.).
M. в переменном электромагнитном поле. При прохождении
переменного тока частоты w в M. наблюдается неоднородное распределение
тока по образцу: ток сосредоточен вблизи поверхности образца на расстоянии порядка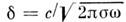 (см.
Скин-эффект ).Для Cu глу-
(см.
Скин-эффект ).Для Cu глу-
бина скин-слоя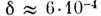 см
при
см
при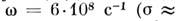
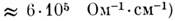 (см. Высокочастотная проводимость).
(см. Высокочастотная проводимость).
При падении эл--магн. волны на поверхность M.
скин-эффект проявляется как в том, что эл--магн. поле затухает на глубине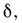 так
и в том, что оно почти полностью отражается от поверхности M.: коэф. отражения
так
и в том, что оно почти полностью отражается от поверхности M.: коэф. отражения
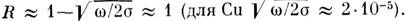
Приведённые оценки справедливы в случае нормального
скин-эффекта, когда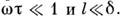 При
T = 300 К эти условия выполняются вплоть до оптич. частот
При
T = 300 К эти условия выполняются вплоть до оптич. частот
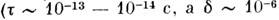 см при
см при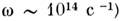
При низких темп-pax и для чистых образцов M.
условие l << d часто не выполняется (даже если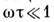 ).
При этом имеет место аномальный скин-эффект,
при к-ром d и R не зависят от l, и тем самым от T.
).
При этом имеет место аномальный скин-эффект,
при к-ром d и R не зависят от l, и тем самым от T.
При низкой температуре M., помещённый в достаточно
сильное магн. поле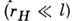 ,
обладает MH. свойствами, характерными для
плазмы: в нём могут распространяться разнообразные слабозатухающие волны (геликоны,
магнитоплазменные волны, допплероны и др.). Коэф. R "ощущает"
циклотронный резонанс (при равенстве частоты поля
,
обладает MH. свойствами, характерными для
плазмы: в нём могут распространяться разнообразные слабозатухающие волны (геликоны,
магнитоплазменные волны, допплероны и др.). Коэф. R "ощущает"
циклотронный резонанс (при равенстве частоты поля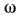 целому
кратному циклотронной частоты
целому
кратному циклотронной частоты 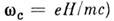 (см. Плазма твёрдых тел). В нек-рых M. (напр.,
в щелочных) удаётся наблюдать электронный парамагнитный резонанс на электронах
проводимости и спиновые волны.
(см. Плазма твёрдых тел). В нек-рых M. (напр.,
в щелочных) удаётся наблюдать электронный парамагнитный резонанс на электронах
проводимости и спиновые волны.
Оптические свойства. Для эл--магн. волн оптич.
диапазона M., как правило, непрозрачны. Характерный блеск - следствие практически
полного отражения света поверхностью M., обусловленного тем, что диэлектрическая
проницаемость электронного газа e при оптич. частотах отрицательна.
Диэлектрич. проницаемость M. 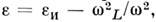 где
где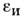 - диэлектрич.
проницаемость ионного остова,
- диэлектрич.
проницаемость ионного остова,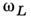 -
плазменная (ленгмюровская) частота электронов. Плазменные частоты могут быть
экспериментально определены по характеристич. потерям энергии быстрых электронов
(с энергией
-
плазменная (ленгмюровская) частота электронов. Плазменные частоты могут быть
экспериментально определены по характеристич. потерям энергии быстрых электронов
(с энергией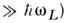 при
прохождении через металлич. плёнку. Они теряют энергию на возбуждение плазмонов
- квантов колебаний электронной жидкости с частотой
при
прохождении через металлич. плёнку. Они теряют энергию на возбуждение плазмонов
- квантов колебаний электронной жидкости с частотой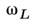 (табл.
8).
(табл.
8).
Табл. 8.- Энергия плазмона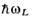 для
некоторых металлов
для
некоторых металлов

Наличием электронов проводимости обусловлено
также экранирование в M. зарядов (напр., заряженных примесей) на характерном
расстоянии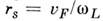 (Дебая - Хюккеля радиус), имеющем атомный масштаб. При взаимодействии света
с электронами M. важную роль играет т. н. внутр. фотоэффект, т. е. вынужденные
(за счёт поглощения фотонов) переходы электронов из зоны в зону. Как правило,
именно внутр. фотоэффект определяет коэф. поглощения излучения видимого и УФ-диапазонов
и изменение проводимости M. под воздействием света (см. Фотопроводимость). Чем выше
(Дебая - Хюккеля радиус), имеющем атомный масштаб. При взаимодействии света
с электронами M. важную роль играет т. н. внутр. фотоэффект, т. е. вынужденные
(за счёт поглощения фотонов) переходы электронов из зоны в зону. Как правило,
именно внутр. фотоэффект определяет коэф. поглощения излучения видимого и УФ-диапазонов
и изменение проводимости M. под воздействием света (см. Фотопроводимость). Чем выше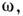 тем
меньшую роль во взаимодействии света с M. играют электроны проводимости: для
УФ- и рентг. диапазонов M. мало отличается от диэлектрика. Отражение плоскополяризов.
света от поверхности M. сопровождается поворотом плоскости поляризации и появлением
эллиптич. поляризации. Это явление используется для техн. целей и для определения
оптич. констант M. (см. Металлооптика, Отражение света, Поляризация света).
тем
меньшую роль во взаимодействии света с M. играют электроны проводимости: для
УФ- и рентг. диапазонов M. мало отличается от диэлектрика. Отражение плоскополяризов.
света от поверхности M. сопровождается поворотом плоскости поляризации и появлением
эллиптич. поляризации. Это явление используется для техн. целей и для определения
оптич. констант M. (см. Металлооптика, Отражение света, Поляризация света).
Лит.: Крэкнелл А.,Квей Чонг Уонг, Поверхность
Ферми, пер. с англ., M., 1978; Абрикосов А. А., Основы теории металлов, M.,
1987.
M. И. Каганов, В. С. Эдельман.
Механические свойства. Многие M. и сплавы обладают
одновременно высокой механич. прочностью и высокой пластичностью, что обусловливает
их широкое применение в качестве конструкц. материалов. Изменение линейных размеров
M. в результате пластич. деформации при T = 300 К достигает десятков,
а иногда сотен % (сверхпластичность).
Механич. свойства исследуют, измеряя зависимость
механич. напряжение - деформация (рис. 8). Изменение формы образца в процессе
деформации показано для трёх характерных участков диаграммы. Участок OA соответствует
прямой пропорциональности между нагрузкой и удлинением и обратимости деформации
(упругая область; см. Гука закон ).На нелинейном участке AB нагрузка
продолжает увеличиваться с меньшей скоростью, деформация необратима, но распределена
равномерно по длине образца. На участке BC нагрузка уменьшается вследствие
локального уменьшения поперечного сечения образца в его центр, части. Образование
"шейки" характерно для пластичных M. В конце этого участка наступает
разрушение (точка С).
Сопротивление M. воздействию внеш. механич. сил
описывается модулями упругости. Характерный порядок их величины для M.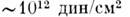 (1011
Н/м2), различные компоненты тензора модулей упругости одного M. отличаются
в неск. раз, а у разных M. могут отличаться в десятки раз. Поликристаллы при
отсутствии текстуры в упругом отношении изотропны, и для описания их
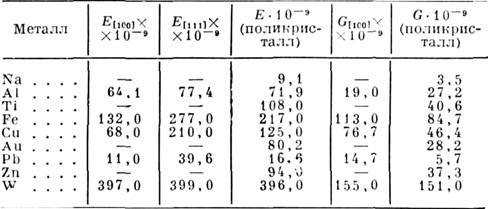
механич. свойств достаточно двух модулей, напр, модуля Юнга E и модуля
сдвига G (табл. 9).
(1011
Н/м2), различные компоненты тензора модулей упругости одного M. отличаются
в неск. раз, а у разных M. могут отличаться в десятки раз. Поликристаллы при
отсутствии текстуры в упругом отношении изотропны, и для описания их
механич. свойств достаточно двух модулей, напр, модуля Юнга E и модуля
сдвига G (табл. 9).
Табл. 9.- Модули упругости E и модули
сдвига G (в Н/м2) для металлических монокристаллов и поликристаллов
Величина упругих модулей определяется межатомными
взаимодействиями и потому коррелирует с энергией связи U, необходимой
для разделения твёрдого тела на отд. нейтральные атомы при T = OK. Так,
у VV энергия связи на 1 атом равна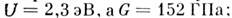
у Cs энергия связи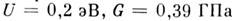 (у
Cs - наименьший среди M. модуль сдвига).
При увеличении температуры T модули упругости монотонно убывают, изменение
модуля в интервале от 0 К до Тпл составляет ок. 50%
исходного значения. В области упругого поведения в M. возможно проявление внутреннего
трения. M. с низким уровнем внутр. трения, слабо рассеивающие энергию колебаний,
используются при изготовлении акустич. резонаторов музыкальных инструментов.
(у
Cs - наименьший среди M. модуль сдвига).
При увеличении температуры T модули упругости монотонно убывают, изменение
модуля в интервале от 0 К до Тпл составляет ок. 50%
исходного значения. В области упругого поведения в M. возможно проявление внутреннего
трения. M. с низким уровнем внутр. трения, слабо рассеивающие энергию колебаний,
используются при изготовлении акустич. резонаторов музыкальных инструментов.
Пластич. деформация M. осуществляется относит,
сдвигом (скольжением) параллельных атомных плоскостей и двойникованием (см.
Пластичность ).Предел текучести в монокристаллах анизотропен и зависит
от плоскости и направления, вдоль к-рых происходит скольжение. Совокупность
плоскости и направления скольжения образует систему скольжения. В каждом кристалле
существует система скольжения, в к-рой критич. величина внеш. напряжения для
начала скольжения минимальна (напряжение лёгкого скольжения  табл. 10).
табл. 10).
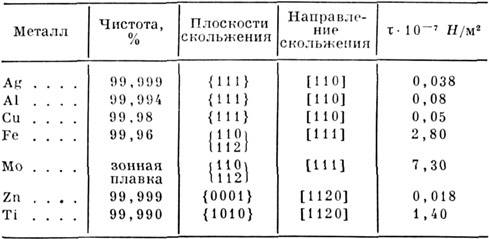
Табл. 10.- Напряжение лёгкого скольжения при
300 К
В случае механич. двойникования происходит
сдвиг области кристалла в положение, зеркальное относительно области, не испытавшей
сдвиг. Механич. напряжение, необходимое для возникновения двойника, больше,
чем для обычного скольжения. Время образования двойника составляет неск. мкс.
Теоретически сопротивление M. пластич. деформации
и разрушению составляет 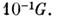 Экспериментально пластич. деформации и разрушение
наблюдаются при напряжениях
Экспериментально пластич. деформации и разрушение
наблюдаются при напряжениях Это
различие обусловлено существованием дислокаций. Движение дислокаций вдоль определ. плоскостей в кристалле обеспечивает сдвиг
одной части кристалла относительно другой. Сопротивление решётки движению дислокаций
(сила Пайерлса - Набарро) составляет
Это
различие обусловлено существованием дислокаций. Движение дислокаций вдоль определ. плоскостей в кристалле обеспечивает сдвиг
одной части кристалла относительно другой. Сопротивление решётки движению дислокаций
(сила Пайерлса - Набарро) составляет 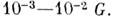 Силы Пайерлса - Набарро в M. с чисто металлич.
связью малы, т. к. эта связь не является направленной и слабо меняется при изменении
атомной конфигурации вблизи дислокации. В M. с компонентой ковалентной связи, имеющих объёмноцентриров. решётку, сопротивление скольжению несколько больше,
однако всё же мало по сравнению с чисто ковалентными кристаллами (отсюда
высокая пластичность).
Силы Пайерлса - Набарро в M. с чисто металлич.
связью малы, т. к. эта связь не является направленной и слабо меняется при изменении
атомной конфигурации вблизи дислокации. В M. с компонентой ковалентной связи, имеющих объёмноцентриров. решётку, сопротивление скольжению несколько больше,
однако всё же мало по сравнению с чисто ковалентными кристаллами (отсюда
высокая пластичность).
Прочность и пластичность M. обусловлены также
взаимодействием дислокаций между собой и с др. дефектами, примесями и их скоплениями,
границами раздела фаз, включениями др. фаз. Величина этих взаимодействий пропорциональна
G. В процессе развития пластич. деформации происходит "размножение"
дислокации, к-рое приводит к затруднению их движения, т. е. к увеличению сопротивления
металла пластич. деформации (деформационное упрочнение, или наклёп). Сопротивление
M. пластич. деформации возрастает с увеличением степени деформации как 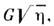 где
где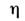 - плотность
дислокаций. В отожжённых (недеформированных) металлич. кристаллах плотность
дислокаций
- плотность
дислокаций. В отожжённых (недеформированных) металлич. кристаллах плотность
дислокаций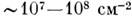 ,
сильная пластич. деформация приводит к её
увеличению до 1011-1012 см-2.
,
сильная пластич. деформация приводит к её
увеличению до 1011-1012 см-2.
При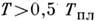 в
пластич. деформации начинают играть существ,
роль точечные дефекты, в первую очередь вакансии, к-рые, оседая на дислокациях,
приводят к их выходу из плоскостей скольжения. Если этот процесс достаточно
интенсивен, то деформация не сопровождается упрочнением: M. "течёт"
с пост, скоростью при неизменной нагрузке (ползучесть). Релаксация напряжений
и разрядка дислокац. структуры обеспечивают высокую пластичность M. при их горячей
обработке. Отжиг сильно деформиров. металлич. монокристаллов нередко приводит
к образованию поликристаллов с малой плотностью дислокаций внутри зёрен.
в
пластич. деформации начинают играть существ,
роль точечные дефекты, в первую очередь вакансии, к-рые, оседая на дислокациях,
приводят к их выходу из плоскостей скольжения. Если этот процесс достаточно
интенсивен, то деформация не сопровождается упрочнением: M. "течёт"
с пост, скоростью при неизменной нагрузке (ползучесть). Релаксация напряжений
и разрядка дислокац. структуры обеспечивают высокую пластичность M. при их горячей
обработке. Отжиг сильно деформиров. металлич. монокристаллов нередко приводит
к образованию поликристаллов с малой плотностью дислокаций внутри зёрен.
При увеличении плотности дислокаций образуются
их скопления, являющиеся концентраторами внутр. напряжений. Вследствие этого
в области скопления дислокаций могут образоваться микротрещины, рост к-рых приводит
к разрушению. В отличие от др. твёрдых тел в M. достаточные для образования
трещин внутр. напряжения развиваются при больших степенях пластич. деформации.
В M. до разрушения в большинстве случаев происходит заметное развитие пластич.
деформации, приводящее к ослаблению концентрации напряжений и торможению роста
трещины (вязкое разрушение). Если движение дислокаций вблизи вершины трещины
затруднено, концентрация напряжений ослабляется незначительно, происходит хрупкое
разрушение.
Механич. характеристики M. можно изменять в широких
пределах термич. и механич. обработкой, а также введением примесей (легированием).
Улучшение механич. свойств M. основано на изменении условий движения, размножения
и торможения дислокаций. В качестве материалов для изготовления конструкций
чистые M. непригодны из-за их малой прочности. Напр., предел прочности Fe (техн.
чистоты)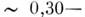 0,35
ГПа, тогда как высокопрочные легиров. стали (сплавы Fe с С и др. M.) имеют предел
прочности от 1,5 до 4,5 ГПа (см. Механические свойства материалов).
0,35
ГПа, тогда как высокопрочные легиров. стали (сплавы Fe с С и др. M.) имеют предел
прочности от 1,5 до 4,5 ГПа (см. Механические свойства материалов).

В. С. Крапошин
|
|