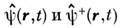 (где
г - координата, t - время), удовлетворяющими для частиц, подчиняющихся
статистике Бозе - Эйнштейна, перестановочным соотношениям
(где
г - координата, t - время), удовлетворяющими для частиц, подчиняющихся
статистике Бозе - Эйнштейна, перестановочным соотношениямМакроскопические квантовые эффекты - совокупность явлений, в к-рых характерные особенности квантовой механики непосредственно
проявляются в поведении макроскопич. объектов. В большинстве случаев поведение
макроскопических (содержащих большое число атомов) тел с высокой точностью описывается
классич. механикой, так что характерная для квантовой механики величина - постоянная
Планка h - не входит в управляющие этим поведением ур-ния. Однако при
низких темп-pax существует важный класс вполне макроскопич. экспериментов, в
результаты к-рых постоянная Планка входит в явном виде н может быть из них непосредственно
измерена. Б. ч. этих экспериментов связана со сверхтекучестью жидкого
гелия и сверхпроводимостью металлов.
В квантовой механике состояние и движение системы
описывается с помощью волновой функции, не имеющей классич. аналога. В рассматриваемых
явлениях, однако, волновая функция проявляется как наблюдаемая макроскопич. величина.
Это возможно в том случае, когда в системе имеется большое число частиц, находящихся
в одном и том же квантовом состоянии.
В матем. аппарате квантовой теории уничтожение
и рождение частиц описывается операторами вторичного квантования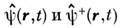 (где
г - координата, t - время), удовлетворяющими для частиц, подчиняющихся
статистике Бозе - Эйнштейна, перестановочным соотношениям
(где
г - координата, t - время), удовлетворяющими для частиц, подчиняющихся
статистике Бозе - Эйнштейна, перестановочным соотношениям
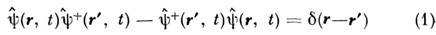
 - дельта-функция Дирака]. Если в к--л. квантовом состоянии системы находится
много частиц, матричные элементы операторов в левой части равенства велики и
некоммутативностью операторов, т. е. правой частью (1), можно пренебречь. Тогда
операторы
- дельта-функция Дирака]. Если в к--л. квантовом состоянии системы находится
много частиц, матричные элементы операторов в левой части равенства велики и
некоммутативностью операторов, т. е. правой частью (1), можно пренебречь. Тогда
операторы 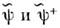 переходят
в коммутирующие друг с другом классич. функции координат и времени
переходят
в коммутирующие друг с другом классич. функции координат и времени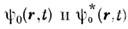 .
функцию
.
функцию 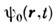 можно
назвать макроскопич. волновой функцией рассматриваемых частиц, н наличие такой
функции является свидетельством имеющейся в этом случае макроскопич. квантовой
когерентности. В простейшем виде такая ситуация реализуется в классич. эл--магн.
поле, к-рое можно рассматривать как совокупность большого числа фотонов, находящихся
в близких квантовых состояниях. Однако особенно интересные явления происходят
в случае, когда в одном состоянии находится большое число "обыкновенных"
частиц, напр, атомов, число к-рых, в отличие от числа фотонов, сохраняется.
можно
назвать макроскопич. волновой функцией рассматриваемых частиц, н наличие такой
функции является свидетельством имеющейся в этом случае макроскопич. квантовой
когерентности. В простейшем виде такая ситуация реализуется в классич. эл--магн.
поле, к-рое можно рассматривать как совокупность большого числа фотонов, находящихся
в близких квантовых состояниях. Однако особенно интересные явления происходят
в случае, когда в одном состоянии находится большое число "обыкновенных"
частиц, напр, атомов, число к-рых, в отличие от числа фотонов, сохраняется.
Это осуществляется в сверхтекучем 4He.
При темп-pax ниже температуры перехода в гелии происходит Возе - Эйнштейна
конденсация, состоящая в том, что конечная доля атомов гелия переходит в
низшее (при данных макроскопич. условиях) квантовое состояние. Будучи пропорциональным
полному числу атомов в теле, число атомов в конденсате велико, так что, согласно
сказанному выше, они описываются классич. "волновой ф-цпей конденсата"
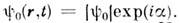 Для покоящегося
гелия
Для покоящегося
гелия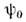 - просто
постоянная. Но если гелий движется,
- просто
постоянная. Но если гелий движется, 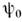 зависит от координат и времени, причём скорость сверхтекучего движения
зависит от координат и времени, причём скорость сверхтекучего движения 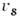 связана
с фазой ее волновой функции ф-лой
связана
с фазой ее волновой функции ф-лой
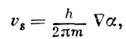 (2)
(2)
где m - масса атома гелия. Ф-ла (2) выражает
макро-скопич. квантовый характер движения сверхтекучего гелия. Действительно,
из (2) следует, что циркуляция скорости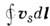 по
нек-оому замкнутому контуру в жидкости равна
по
нек-оому замкнутому контуру в жидкости равна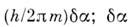 -
изменение фазы a при
-
изменение фазы a при
обходе контура, к-рое вследствие однозначности
функции 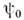 должно
равняться 2pn, где n - целое число. T. о., в сверхтекучем
гелии
должно
равняться 2pn, где n - целое число. T. о., в сверхтекучем
гелии

Это означает наличие в жидкости квантованных
вихревых нитей. При приближении к нити скорость vs возрастает
как 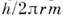 , где r
- расстояние до нити. Вокруг каждой нити имеется циркуляция скорости, равная
h/m.
, где r
- расстояние до нити. Вокруг каждой нити имеется циркуляция скорости, равная
h/m.
Такой характер движения сверхтекучего гелия даёт
возможность измерения постоянной Планка в прямом макроскопич. механич. эксперименте,
поставленном У. Ф. Вайненом в 1960 [1]. По оси заполненной жидким гелием трубочки
радиуса R = 2 мм была укреплена струна с собств. частотой 500 Гц. Система
помещалась между полюсами магнита, и импульс тока приводил струну в колебания
в нек-рой плоскости. Такое колебание можно рассматривать как совокупность двух
цир-кулярно поляризов. колебаний, к-рые в случае покоящегося гелия имеют одну
и ту же частоту v. Затем трубочка приводилась во вращение, и вокруг струны
возникало движение гелия с циркуляцией him. При этом на струну действовала
сила, аналогичная подъёмной силе крыла и равная на единицу длины струны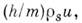 где
где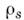 -
плотность сверхтекучей части гелия, и - скорость струны. Эта сила приводила к расщеплению частот циркулярно поляризов.
колебаний. Можно показать, что
-
плотность сверхтекучей части гелия, и - скорость струны. Эта сила приводила к расщеплению частот циркулярно поляризов.
колебаний. Можно показать, что 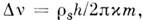 где к - масса единицы длины струны. В эксперименте колебание проявлялось
в виде биений сигнала с частотой 0,45 Гц.
где к - масса единицы длины струны. В эксперименте колебание проявлялось
в виде биений сигнала с частотой 0,45 Гц.
Др. способом определения постоянной Планка в
этом эксперименте может служить измерение угл. скорости W вращения трубочки,
при которой впервые появляются биения. Согласно теории,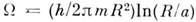 ,
a ~ 4·10~8 см; в условиях эксперимента эта величина составляла
0,2 рад*с-1.
,
a ~ 4·10~8 см; в условиях эксперимента эта величина составляла
0,2 рад*с-1.
Отметим, что для эффектов данного типа характерна
линейная зависимость наблюдаемой величины от h.
Ряд M. к. э. наблюдается в сверхпроводящих металлах.
Поскольку электроны подчиняются статистике Ферми - Дирака, в одном квантовом
состоянии не может находиться больше одного электрона. Однако при переходе в
сверхпроводящее состояние в металле образуются пары из двух электронов с противоположными
импульсами и спинами - т. н. куперовские пары. Эти пары, являющиеся бозонами,
ниже точки перехода находятся в состоянии бозе-конденсации и характеризуются
макроскопич. волновой функцией 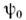
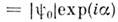 . Для описания M. к. э. в сверхпроводниках существенно поведение
. Для описания M. к. э. в сверхпроводниках существенно поведение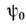 при калибровочных (градиентных) преобразованиях векторного А и скалярного
f потенциалов эл--магн. поля. Волновая функция пары ведёт себя при этих преобразованиях
как волновая функция частицы с зарядом 2е (е - заряд электрона). Соответственно
никакие имеющие прямой физ. смысл величины не должны меняться при след, преобразовании
A, f и фазы волновой функции а:
при калибровочных (градиентных) преобразованиях векторного А и скалярного
f потенциалов эл--магн. поля. Волновая функция пары ведёт себя при этих преобразованиях
как волновая функция частицы с зарядом 2е (е - заряд электрона). Соответственно
никакие имеющие прямой физ. смысл величины не должны меняться при след, преобразовании
A, f и фазы волновой функции а:
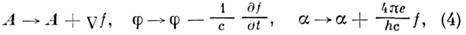
где f - произвольная функция координат и
времени.
Характерным M. к. э. в сверхпроводнике является
квантование магнитного потока .Поток индукции через отверстие в массивном
сверхпроводнике может быть равен лишь целому кратному от нек-рого "кванта
потока" Ф0. Для доказательства рассмотрим охватывающий отверстие
контур в глубине сверхпроводника (толщиной
больше глубины проникновения магн. поля), где магн. поле, а следовательно, и
плотность тока отсутствуют (магн. поле вытесняется из сверхпроводника вследствие
эффекта Мейснера). Сверхпроводящий ток, как и сверхтекучая скорость в гелии,
связан с градиентом фазы волновой функции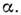 Поэтому
при полном отсутствии магн. поля, когда можно считать, что
Поэтому
при полном отсутствии магн. поля, когда можно считать, что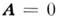 во
всём пространстве, условие отсутствия тока имеет вид
во
всём пространстве, условие отсутствия тока имеет вид 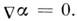 Но при наличии
Но при наличии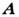 это
соотношение не может быть верным, т. к. оно нарушается при преобразовании (4).
Инвариантное относительно (4) условие, очевидно, имеет вид
это
соотношение не может быть верным, т. к. оно нарушается при преобразовании (4).
Инвариантное относительно (4) условие, очевидно, имеет вид
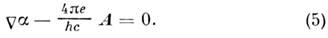
Проинтегрировав (5) по указанному контуру и учитывая,
что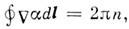 а поток
магн. индукции
а поток
магн. индукции
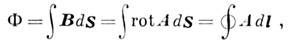
получаем
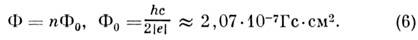
Наличие множителя 2 в знаменателе непосредственно
связано со спариванием электронов в сверхпроводнике. Тот факт, что для вывода
(6) было достаточно рассмотреть область пространства, где магн. поле отсутствует,
ярко демонстрирует неклассич. характер эффекта.
Квантование потока было экспериментально обнаружено
в 1961 Б. С. Дивером и У. M. Фэрбанком [2], а также P. Доллом и M. Набауэром
[3]. В этих экспериментах использовались оловянные трубочки диам. (1 -1,5)·10-3
см и длиной порядка 1 см. Когда в трубочке был "вморожен" один квант
потока, магн. поле в ней равнялось примерно 0,1 Гс. В опытах можно было измерить
магн. момент трубочки, а следовательно, и постоянную Планка.
Др. типа M. к. э. возможны в сверхпроводниках
2-го рода. Достаточно сильное магн. поле проникает в них в виде отд. нитей -
вихрей Абрикосова (см. Квантованные вихри)с толщиной порядка глубины
проникновения слабого поля в сверхпроводник. В каждой нити заключён один квант
потока.
Очень важные для техн. приложений M. к. э. основаны
на Джозефсона эффекте [4,5]. Они наблюдаются в сверхпроводящих цепях,
в к-рых имеются джозефсо-новские контакты - тонкие слои диэлектрика (или несверхпроводящего
материала), разделяющие два сверхпроводника. Квантовое туннелирование позволяет
электронам переходить из одного сверхпроводника в другой, так что в цепи может
течь сверхпроводящий ток. Величина этого тока I должна определяться разностью
фаз волновой функции сверхпроводящих пар по обе стороны контакта:
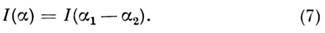
функция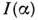 строго
периодична с периодом
строго
периодична с периодом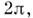 поскольку
при изменении фазы на
поскольку
при изменении фазы на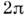 волновая
функция
волновая
функция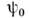 не меняется.
Кроме того, она нечётна, т. к. изменение знака a соответствует в квантовой
механике обращению времени, что меняет знак тока.
не меняется.
Кроме того, она нечётна, т. к. изменение знака a соответствует в квантовой
механике обращению времени, что меняет знак тока.
Из M. к. э. в джозефсоповских контактах рассмотрим
нестационарный эффект Джозефсона, к-рый наблюдается при приложении к контакту
постоянной разности потенциалов (этот эффект экспериментально обнаружен И. M.
Дмитренко и И. К. Янсоном в 1964). В отсутствие разности потенциалов явления
в цепи стационасны. так что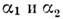 не
зависят от времени:
не
зависят от времени: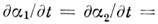
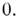 При наличии скалярного потенциала эти равенства обобщаются так, чтобы они оставались
инвариантными при преобразованиях (4):
При наличии скалярного потенциала эти равенства обобщаются так, чтобы они оставались
инвариантными при преобразованиях (4):
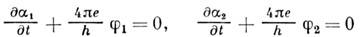
и
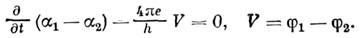
Если У не зависит от времени, то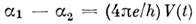 ,
,
что даёт для тока

T. о., если к контакту приложено пост, напряжение,
в цепи течёт строго периодпч. ток. Более подробная теория показывает, что ток
/(а) в (7) и (8) является синусоидальным с частотой 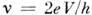 .
Монохроматичность тока нарушается только флуктуациями напряжения в цепи. Рассмотренный
эффект позволил уточнить известное значение постоянной Планка.
.
Монохроматичность тока нарушается только флуктуациями напряжения в цепи. Рассмотренный
эффект позволил уточнить известное значение постоянной Планка.
На основе джозефсоновских контактов созданы получившие
широкое распространение сверхпроводящие квантовые интерферометры - СКВИДы. Принципиальная
схема такого прибора содержит включённое в электрич. цепь, разрезанное в двух
местах сверхпроводящее кольцо, причём в разрезы вставлены джозеф-соновские контакты.
Рассуждения, аналогичные проведённым при выводе (6), показывают, что если кольцо
пронизывает поток магн. индукции Ф, то пазности фаз на контактах будут отличаться
на 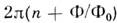 . Это приводит
к зависимости тока в цепи от потока Ф:
. Это приводит
к зависимости тока в цепи от потока Ф:
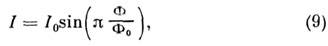
что позволяет измерять изменения потока в доли
кванта Ф0.
Своеобразна ситуация в сверхтекучем 3He.
Атомы 3He являются фермионами, и его сверхтекучесть связана с образованием
куперовских пар. В 3He эти пары образуются, в отличие от пар электронов
в обычных сверхпроводниках, с орбитальным и спиновым угл. моментами, равными
единице. Это приводит к тому, что волновая функция пар в 3He является
не скаляром, а тензором 2-го ранга, что обусловливает анизотропию сверхтекучего
3He и большое разнообразие в нём M. к. э.
В 1980 обнаружен новый тип явлений, к-рый также
носит характер M. к. э.,- квантовый Холла эффект .Он наблюдается при
низких темп-pax в инверсном слое - двумерной системе электронов, удерживаемых
вблизи границы раздела двух полупроводников перпендикулярным к границе электрич.
нолем. При наложении перпендикулярного слою магн. поля Н энерге-тич.
спектр электронов разбивается на дискретные квантовые уровни. В вырожденном электронном
на каждом уровне может находиться (на единице поверхности слоя) eH/hc электронов.
Холловская компонента тензора поверхностной проводимости sxy в сильном магн. поле равна -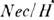 ,
где N - поверхностная плотность электронов. Если уровень Ферми лежит
между n-м и (n + 1)-M квантовыми уровнями, то
,
где N - поверхностная плотность электронов. Если уровень Ферми лежит
между n-м и (n + 1)-M квантовыми уровнями, то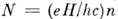 и
и

т. е. 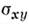 - квантована. Число электронов, а следовательно, и положение уровня Ферми можно
менять, изменяя напряжение перпендикулярного электрич. поля V. При тех
значениях F, при к-рых уровень Ферми лежит указанным выше образом, на кривой
sxy(V)
должен иметься плоский участок - "плато" - при квантованном
значении
- квантована. Число электронов, а следовательно, и положение уровня Ферми можно
менять, изменяя напряжение перпендикулярного электрич. поля V. При тех
значениях F, при к-рых уровень Ферми лежит указанным выше образом, на кривой
sxy(V)
должен иметься плоский участок - "плато" - при квантованном
значении 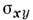 Приведённый
вывод не учитывает наличия примесей, к-рые могут связывать часть электронов,
и электрон-электронного взаимодействия. На опыте, однако, наблюдаются отчётливые
"плато", причём sху на них равно значениям (10) с очень высокой точностью. Кроме того, имеются,
по-видимому, "плато" при дробных рациональных значениях п, что
можно интерпретировать как существование квазичастиц с дробными значениями электрич.
заряда. Полное теоретпч. объяснение этих
особенностей эксперимента пока отсутствует. Возможно, что кулоновское взаимодействие
между электропамп приводит к особого рода квантовой когерентности в этой системе.
Приведённый
вывод не учитывает наличия примесей, к-рые могут связывать часть электронов,
и электрон-электронного взаимодействия. На опыте, однако, наблюдаются отчётливые
"плато", причём sху на них равно значениям (10) с очень высокой точностью. Кроме того, имеются,
по-видимому, "плато" при дробных рациональных значениях п, что
можно интерпретировать как существование квазичастиц с дробными значениями электрич.
заряда. Полное теоретпч. объяснение этих
особенностей эксперимента пока отсутствует. Возможно, что кулоновское взаимодействие
между электропамп приводит к особого рода квантовой когерентности в этой системе.

Л. П. Питаевский
|
|