Глоссарий по физике

Синхронизация колебаний

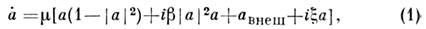
Синхронизация колебаний - согласование частот, фаз или др. характеристик сигналов, генерируемых взаимодействующими колебательными системами. Различают взаимную С. к., когда парциальные подсистемы перестраивают режим колебаний друг друга, и внешнюю (вынужденную) С. к., когда характеристики колебаний системы (систем) изменяются под действием внеш. силы. Вынужденную синхронизацию по частоте колебаний, т. е. навязывание системе, характеризующейся в автономном режиме одной частотой колебаний, др. частоты, определяемой внеш. силой, называют захватыванием частоты. Захватывание частоты - простейший пример явления синхронизации, к-рый был описан ещё X. Гюйгенсом (Ch. Huygens) в связи с ускорением или замедлением хода часов, висящих на независимо колеблющейся балке (см., напр., [1]).

Наиб. полно развита теория С. к. для квазигармонических колебаний в слабо нелинейных системах [2-4].

В частности, усреднённые по периоду внеш. силы ур-ния для комплексной амплитуды а нелинейного генератора с одной степенью свободы, находящегося под действием слабой гармонической силы, имеют вид:

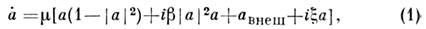
где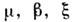 - действительные параметры: 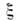- расстройка между частотой автоколебаний и частотой внеш. силы, 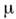- коэф. усиления в автономном генераторе, 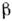- нелинейный сдвиг частоты. Режиму С. к. соответствует устойчивое положение равновесия системы (1). В исходном же (3-мерном) фазовом пространстве режиму С. к. отвечает устойчивый предельный цикл .При увеличении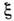 режим С. к. либо перестаёт существовать (при слабых внеш. сигналах), либо теряет устойчивость (в случае сильных сигналов). Область значений расстроек, для к-рых реализуется режим С. к., наз. полосой захватывания. Граница полосы захватывания находится из (1): из условия существования режима С. к. (а = 0) устанавливается резонансная кривая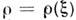 , где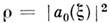 - интенсивность автоколебаний в режиме С. к., и по линеаризованному ур-нию определяется устойчивость этого режима. На рис. 1 показаны полосы захватывания в случаях слабых и сильных сигналов. На рис. 2 изображены последовательности фазовых портретов на плоскости (Rea, Ima),. отвечающих (1) при разных значениях расстройки. При переходе через границу области захватывания режим С. к. сменяется режимом биений - наблюдается бифуркация Андронова - Хопфа (при сильных сигналах) или бифуркация рождения предельного цикла из петли, сепаратрисы седло - узел (при слабых сигналах). В исходном (3-мерном) фазовом пространстве переходу к режиму биений отвечает рождение притягивающего двумерного тора с квазипериодич. обмоткой. Аналогичным образом можно исследовать С. к. ансамбля генераторов, находящихся под действием одной и той же внеш. гармонической силы [5, 6].

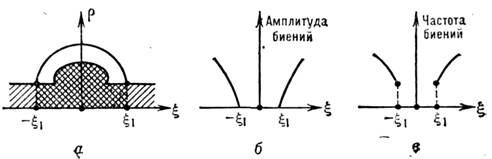
Рис. 1.

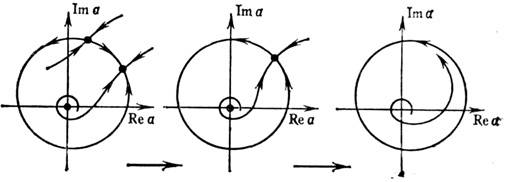
Рис. 2.

Явление взаимной синхронизации генераторов квазигармонических колебаний в простейшем случае бигармонического резонанса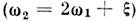 может быть исследовано в рамках системы ур-ний для комплексных амплитуд а_1,2 взаимодействующих мод в автогенераторе с двумя степенями свободы:

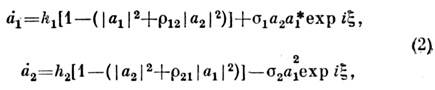
где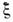 - расстройка от точного резонанса, h_1,2 - инкременты каждой из мод,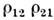 - параметры, характеризующие конкуренцию мод, а 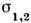- их резонансное взаимодействие. Здесь также режиму С. к. отвечает устойчивое состояние равновесия, граница области устойчивости к-рого и определяет границу области взаимной синхронизации [3]. Взаимная синхронизация наблюдается в системах с числом степеней свободы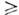 2, и во многих ситуациях после разрушения режима С. к. возможно возникновение стохастических автоколебаний (см. Стохастические колебания ).Явление С. к. наблюдается не только в случае, когда частоты парциальных генераторов близки друг к другу, но и когда они близки к кратным друг друга (синхронизация на гармониках и субгармониках). Именно за счёт взаимной синхронизации мод оптич. резонатора удаётся реализовать режим генерации ультракоротких импульсов в лазерах [7].

В сильно нелинейном случае усреднённое описание, приводящее к ур-ниям типа (1) и (2), не адекватно задаче, и здесь используется качеств. теория линамических систем. В этой теории явление синхронизации периодич. колебаний двух автоколебат. систем можно описать следующим образом. Каждой из систем свойственны периодич. автоколебания, т. е. в ее фазовом пространстве имеется устойчивый предельный цикл - L₁ и L₂ соответственно.

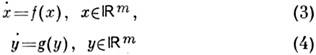
Система

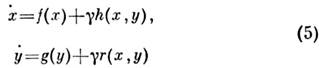
при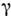 = 0 будет иметь притягивающий двумерный тор 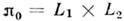(каждая система колеблется независимо от другой). При возрастании параметра связи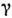движение в парциальных подсистемах системы (5) перестаёт быть независимым, что отвечает бифуркациям на торе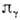 [остающемся аттрактором для системы (5)]. В частности, явлению синхронизации отвечает рождение устойчивого предельного цикла на этом торе.

Более подробную информацию о перестройках в системе при изменении параметра связи даёт т. н. дьявольская лестница - график зависимости числа вращения системы на торе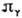 от параметра связи. [Число вращения - это предел отношения фаз бывших независимыми при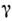 = 0 колебаний парциальных генераторов:

Зависимость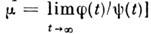 числа вращения от величины параметра связи имеет вид непрерывно уменьшающихся ступеней (рис. 3). Точнее, функция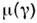 растёт на канторовом множестве. Каждое своё значение, равное отношению целых чисел p/q (синхронизация), число вращения принимает, вообще говоря, на нек-ром интервале, а числа р и q соответствуют номерам гармоник, на к-рых осуществляется взаимная синхронизация. Если следить за изменением не только параметра связи, но и др. параметра (напр., надкритичности в каждом из генераторов), то области синхронизации будут изображаться уже не на прямой, а на плоскости. Обычно эти области имеют вид «языков» [8] (т. н. языки Арнольда [9]) - рис. 4.

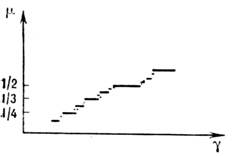
Рис. 3.

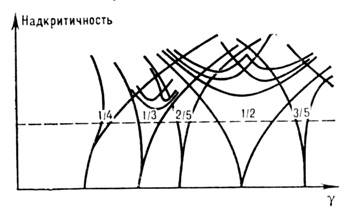
Рис. 4.

Рис. 5.

Взаимное согласование движений свойственно генераторам не только периодических, но и стохастических автоколебаний. Принципиальное отличие от случая периодич. колебаний здесь в том, что движения взаимодействующих неидентичных подсистем согласуются лишь в среднем по времени. При этом могут быть одинаковыми топология проекций странных аттракторов на парциальные подпространства, их размерности, спектры мощности парциальных колебаний. В то же время сами реализации локально по времени могут не совпадать. На рис. 5 представлены странные аттракторы парциальных подсистем в автономном режиме (С = 0) и проекции аттрактора на парциальные подпространства в режиме стохастич. синхронизации (С = 10) для системы, описываемой ур-ниями вида:

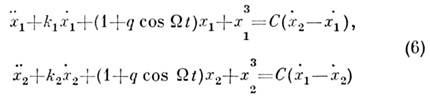
(напр.,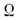 = 2, k₁ = 0,48, k₂ = 0,45 для двух связанных параметрически возбуждаемых генераторов [10]). Степень стохастич. синхронизации может быть различной; в частности, в нек-рых ситуациях, когда взаимодействуют идентичные подсистемы, совпадение парциальных колебаний может быть полным.

Литература по синхронизации колебаний

1. Блехман И. И., Синхронизация в природе и технике, М., 1981;
2. Андронов А. А., Витт А. А., К математической теории захватывания, в кн.: Андронов А. А., Собр. трудов, М., 1956;
3. Блакьер О., Анализ нелинейных систем, пер. с англ., М., 1969;
4. Рабинович М. И., Трубецкой Д. И., Введение в теорию колебаний и волн, М., 1984;
5. Aizawa Y., Synergetic approach to the phenomena of mode-locking in nonlinear systems, «Progr. Theor. Phys.», 1976, v. 56, № 3, p. 703;
6. Рабинович М. И., Стохастические автоколебания и турбулентность, «УФН», 1978, т. 125, с. 123;
7. Квантовая радиофизика, 2 изд., т. 2 - Xанин Я. И., Динамика квантовых генераторов, М., 1975;
8. Арнольд В. И., Малые знаменатели: 1. Об отображениях окружности на себя, «Изв. АН СССР. Сер. мат.», 1961, т. 25, с. 21;
9. Тhоmрsоn J. М., Stewart H. В., Nonlinear dynamics and chaos, N. Y.- [a. o.], 1986; 10) Афраймович В. С., Веричев Н. Н., Рабинович М. И., Стохастическая синхронизация колебаний в диссипативных системах, «Изв. вузов. Радиофизика», 1986, т. 29, № 9, с. 1050.

В. С. Афраймович, М. И. Рабинович

к библиотеке   к оглавлению   FAQ по эфирной физике   ТОЭЭ   ТЭЦ   ТПОИ   ТИ  

Знаете ли Вы, что cогласно релятивистской мифологии "гравитационное линзирование - это физическое явление, связанное с отклонением лучей света в поле тяжести. Гравитационные линзы обясняют образование кратных изображений одного и того же астрономического объекта (квазаров, галактик), когда на луч зрения от источника к наблюдателю попадает другая галактика или скопление галактик (собственно линза). В некоторых изображениях происходит усиление яркости оригинального источника." (Релятивисты приводят примеры искажения изображений галактик в качестве подтверждения ОТО - воздействия гравитации на свет)
При этом они забывают, что поле действия эффекта ОТО - это малые углы вблизи поверхности звезд, где на самом деле этот эффект не наблюдается (затменные двойные). Разница в шкалах явлений реального искажения изображений галактик и мифического отклонения вблизи звезд - 10¹¹ раз. Приведу аналогию. Можно говорить о воздействии поверхностного натяжения на форму капель, но нельзя серьезно говорить о силе поверхностного натяжения, как о причине океанских приливов.
Эфирная физика находит ответ на наблюдаемое явление искажения изображений галактик. Это результат нагрева эфира вблизи галактик, изменения его плотности и, следовательно, изменения скорости света на галактических расстояниях вследствие преломления света в эфире различной плотности. Подтверждением термической природы искажения изображений галактик является прямая связь этого искажения с радиоизлучением пространства, то есть эфира в этом месте, смещение спектра CMB (космическое микроволновое излучение) в данном направлении в высокочастотную область. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА Рыцари теории эфира

10.11.2021 - 12:37: ПЕРСОНАЛИИ - Personalias -> WHO IS WHO - КТО ЕСТЬ КТО - Карим_Хайдаров. 10.11.2021 - 12:36: СОВЕСТЬ - Conscience -> РАСЧЕЛОВЕЧИВАНИЕ ЧЕЛОВЕКА. КОМУ ЭТО НАДО? - Карим_Хайдаров. 10.11.2021 - 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от д.м.н. Александра Алексеевича Редько - Карим_Хайдаров. 10.11.2021 - 12:35: ЭКОЛОГИЯ - Ecology -> Биологическая безопасность населения - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> Проблема государственного терроризма - Карим_Хайдаров. 10.11.2021 - 12:34: ВОЙНА, ПОЛИТИКА И НАУКА - War, Politics and Science -> ПРАВОСУДИЯ.НЕТ - Карим_Хайдаров. 10.11.2021 - 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вадима Глогера, США - Карим_Хайдаров. 10.11.2021 - 09:18: НОВЫЕ ТЕХНОЛОГИИ - New Technologies -> Волновая генетика Петра Гаряева, 5G-контроль и управление - Карим_Хайдаров. 10.11.2021 - 09:18: ЭКОЛОГИЯ - Ecology -> ЭКОЛОГИЯ ДЛЯ ВСЕХ - Карим_Хайдаров. 10.11.2021 - 09:16: ЭКОЛОГИЯ - Ecology -> ПРОБЛЕМЫ МЕДИЦИНЫ - Карим_Хайдаров. 10.11.2021 - 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Екатерины Коваленко - Карим_Хайдаров. 10.11.2021 - 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ - Upbringing, Inlightening, Education -> Просвещение от Вильгельма Варкентина - Карим_Хайдаров.