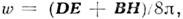Пойнтинга теорема - теорема, описывающая закон сохранения энергии эл--магн. поля. Теорема была доказана в 1884 Дж.
Пойнтингом (J. Н. Poynting). Если продифференцировать по времени плотность
энергии электромагнитного поля в стационарной среде без дисперсии,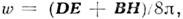
с учётом Максвелла уравнений получим:
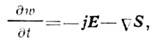
где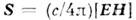
- Пойнтинга вектор, j - плотность тока, Е,
Ни
D,
В - напряжённости и индукции электрич. и магн. полей. В интегральной
форме П. т. принимает вид
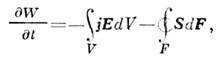
где W - полная энергия эл--магн.
поля, заключённого в объёме V; F - поверхность, ограничивающая объём
V;
dF и dV - элементы поверхности и объёма. Это соотношение получено
в предположении, что заряды не пересекают поверхность F, в противном
случае необходимо учесть поток энергии, переносимый зарядами через F. Интеграл
по объёму описывает работу, совершаемую сторонними эдс над токами проводимости,
и джоулевы потери .Исходя из представления о локализации эл--магн.
энергии в пространстве можно заключить, что она вытекает через поверхность
F из объёма V наружу в кол-ве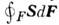
единиц энергии в единицу времени. П. т. применяется чаще всего для определения
потока энергии, теряемой системой заряж. частиц на излучение эл--магн.
волн, однако она справедлива и для статпч. полей. В частности, с помощью
П. т. можно проследить пути поступления энергии в проводник с током.
Для квазимонохроматич. эл--магн. поля
можно ввести комплексные амплитуды E0(r,
t)и
H0(r,
t)электрич. и магн. полей, медленно меняющиеся во времени и пространстве,
напр. E(r,t) = Re{E0 (r, t)х
exp (kr -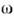t)}, где
k
и -
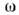волновой вектор и круговая частота. При описании ВЧ-свойств вещества (не
ферромагнетика) с учётом пространств. и временной дисперсии волн нет
необходимости вводить тензор магн. проницаемости, т. е. В = Н (в
СГС). Тензор диэлектрической проницаемости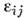можно
разложить на два эрмитовых тензора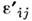и: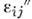
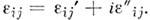В поглощающей среде плотность джоулевых потерь равна
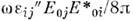(звёздочка означает комплексное сопряжение). В области прозрачности=
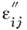0 и средняя по высокой частоте плотность энергии
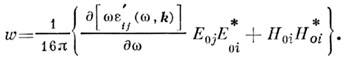
Для этой области П. т. принимает вид
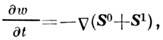
где вектор Пойнтинга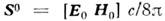
описывает средний поток энергии, переносимый полем, а
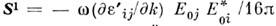- средний поток энергии, переносимый частицами среды. Скорость переноса
энергии в эл--магн. волне совпадает с групповой скоростью волны vгр
и определяется соотношением S=wvгp. Закон сохранения
энергии в поглощающей среде при наличии временной и пространственной дисперсий
не позволяет однозначно интерпретировать входящие в него члены.
Знаете ли Вы, что такое "Большой Взрыв"? Согласно рупору релятивистской идеологии Википедии "Большой взрыв (англ. Big Bang) - это космологическая модель, описывающая раннее развитие Вселенной, а именно - начало расширения Вселенной, перед которым Вселенная находилась в сингулярном состоянии. Обычно сейчас автоматически сочетают теорию Большого взрыва и модель горячей Вселенной, но эти концепции независимы и исторически существовало также представление о холодной начальной Вселенной вблизи Большого взрыва. Именно сочетание теории Большого взрыва с теорией горячей Вселенной, подкрепляемое существованием реликтового излучения..." В этой тираде количество нонсенсов (бессмыслиц) больше, чем количество предложений, иначе просто трудно запутать сознание обывателя до такой степени, чтобы он поверил в эту ахинею. На самом деле взорваться что-либо может только в уже имеющемся пространстве. Без этого никакого взрыва в принципе быть не может, так как "взрыв" - понятие, применимое только внутри уже имеющегося пространства. А раз так, то есть, если пространство вселенной уже было до БВ, то БВ не может быть началом Вселенной в принципе. Это во-первых. Во-вторых, Вселенная - это не обычный конечный объект с границами, это сама бесконечность во времени и пространстве. У нее нет начала и конца, а также пространственных границ уже по ее определению: она есть всё (потому и называется Вселенной). В третьих, фраза "представление о холодной начальной Вселенной вблизи Большого взрыва" тоже есть сплошной нонсенс. Что могло быть "вблизи Большого взрыва", если самой Вселенной там еще не было? Подробнее читайте в FAQ по эфирной физике.
с учётом Максвелла уравнений получим:
- Пойнтинга вектор, j - плотность тока, Е,
Ни
D,
В - напряжённости и индукции электрич. и магн. полей. В интегральной
форме П. т. принимает вид
единиц энергии в единицу времени. П. т. применяется чаще всего для определения
потока энергии, теряемой системой заряж. частиц на излучение эл--магн.
волн, однако она справедлива и для статпч. полей. В частности, с помощью
П. т. можно проследить пути поступления энергии в проводник с током.
t)}, где
k
и
-
волновой вектор и круговая частота. При описании ВЧ-свойств вещества (не
ферромагнетика) с учётом пространств. и временной дисперсии волн нет
необходимости вводить тензор магн. проницаемости, т. е. В = Н (в
СГС). Тензор диэлектрической проницаемости
можно
разложить на два эрмитовых тензора
и
:
В поглощающей среде плотность джоулевых потерь равна
(звёздочка означает комплексное сопряжение). В области прозрачности
=
0 и средняя по высокой частоте плотность энергии
описывает средний поток энергии, переносимый полем, а
- средний поток энергии, переносимый частицами среды. Скорость переноса
энергии в эл--магн. волне совпадает с групповой скоростью волны vгр
и определяется соотношением S=wvгp. Закон сохранения
энергии в поглощающей среде при наличии временной и пространственной дисперсий
не позволяет однозначно интерпретировать входящие в него члены.
