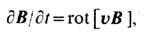
Турбулентность плазмы - хаотическое, детально невоспроизводимое пространственно-временное изменение параметров
плазмы, неустойчивой относительно возбуждения сразу многих её степеней свободы
(колебаний, волн и вихрей разл. типов) до уровня, заметно выше теплового. В отличие
от обычных, тоже нерегулярных, флуктуации вблизи устойчивого термодинамич. равновесия
для турбулентности плазмы характерно именно наличие в плазме неустойчивости, т. е. избыточной
свободной энергии, вводимой в неустойчивые моды (степени свободы) внеш. источниками,
граничными или начальными условиями. За счёт нелинейных взаимодействий эта энергия
перераспределяется между всеми модами и возмущениями разл. пространств. масштабов
и диссипирует в тепло за счёт вязкости, резистивности и пр., достигая быстрозатухающих
мод. В этом отношении турбулентность плазмы сходна с турбулентностью жидкости или газа, но обладает
вследствие кулоновского взаимодействия частиц гораздо большим разнообразием возможных
форм движения, особенно при наличии магн. поля. В соответствии с типом преобладающих
мод и движений плазмы выделяют турбулентность плазмы магнитогидродинамическую (МГД), ленгмюров-скую,
дрейфовую и др.
МГД турбулентность представляет
собой широко распространённый вид турбулентности плазмы в условиях, когда при движении проводящего
газа существенна роль магн. поля. В природных условиях
МГД турбулентность плазмы развивается,
когда геом. масштабы плазмы не очень малы, так что магн. поле является слабозатухающим
и при движении плазмы оно как бы "вморожено" в неё (см. Вмороженность
магнитного поля). Явление вмороженности описывается ур-нием
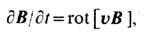
где В и u-соответственно
векторы напряжённости магн. поля и скорости течения плазмы. Несмотря на малость
диссипативных эффектов в подавляющей части объёма, занятого МГД течением, они
принципиально важны в т. н. X-точках - в местах пересечения магн. силовых
линий, перемещаемых и деформируемых потоком плазмы. В этих точках происходит
пересоединение магн. силовых линий с соответствующим изменением топологич.
характеристик магн. поля.
МГД течения характерны
прежде всего для космической плазмы.
Как своеобразную МГД-турбулентность плазмы можно
рассматривать движение межзвёздных облаков, а более компактными объектами с
МГД-турбулентностью плазмы могут служить остатки оболочек сверхновых звёзд, напр. Крабовидная
туманность. В лаб. условиях МГД-турбулентность плазмы наблюдается в установках для магн.
удержания высокотемпературной плазмы: токама ках,
стеллараторах и пинчах, стабилизированных продольным магн. полем. В токамаках
и стеллараторах интенсивная МГД-турбулентность плазмы возникает на периферии
плазменных тороидов;
в более глубоких слоях, где темп-pa плазмы и её электропроводность очень высоки,
МГД-турбулентность плазмы модифицируется в т. н. дрейфовую турбулентность плазмы.
Дрейфовая турбулентность плазмы представляет
собой хаос из дрейфовых волн конечной амплитуды, т. е. таких возмущений, в к-рых
плазма ведёт себя как двухжидкостная среда с разным движением электронов и ионов
в достаточно сильном магн. поле (см. Дрейфовые неустойчивости ).В этом
случае смещение частиц поперёк магн. поля на расстояния, большие соответствующих
ларморовских радиусов, вызывается дрейфом их ларморовских орбит под действием
элек-трич. поля и сил газокинетич. давления плазмы. Дрейфовую Т. п. обычно описывают
не полной системой ур-ний двухжидкостной гидродинамики плазмы, а её более
простыми следствиями, основанными на решении ур-ний поперечного движения электронов
в дрейфовом приближении. В простейшем модельном описании дрейфовой Т. п. используется
приближённое решение ур-ния продольного (вдоль сильного магн. поля) движения
электронов в виде их больцмановского распределения в продольном элек-трич. поле
плазмы. В этом случае динамика дрейфовой Т. п. полностью определяется поведением
электрич. потенциала плазмы j и описывается ур-нием
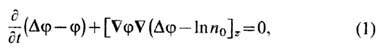
где п0 - плотность невозмущённой пространственно неоднородной плазмы, а пространств.
переменные в операторах 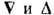 нормированы на ларморовский радиус ионов. Ур-ние (1) позволяет рассчитывать
не только спектр и др. статистич. характеристики дрейфовой Т. п., но описывает
также и регулярные структуры в виде дрейфовых вихрей и солитонов в плазме.
Ур-ние (1) используется не только в теории плазмы, но и при описании многих
др. явлений природы; напр., существует аналогия между дрейфовой турбулентностью
в плазме и турбулентностью волн Рос-сби в атмосферах и океанах планет. В основе
аналогии, роднящей
Большое Красное Пятно в атмосфере Юпитера и дрейфовые вихри в плазме токамака,
лежит схожесть проявления силы Кориолиса во вращающейся планетной атмосфере
и магн. части силы Лоренца в плазме. Как и атм. турбулентность, дрейфовая Т.
п. играет заметную роль в явлениях переноса, приводя к усиленным потокам частиц
и тепла поперёк сильного магн. поля. Существует много диссипативных механизмов
возбуждения дрейфовой турбулентности плазмы, в т. ч. связанных с взаимодействием волн с быстрыми
частицами, инжектируемыми извне или генерируемыми в плазме с помощью дополнит.
нагрева.
нормированы на ларморовский радиус ионов. Ур-ние (1) позволяет рассчитывать
не только спектр и др. статистич. характеристики дрейфовой Т. п., но описывает
также и регулярные структуры в виде дрейфовых вихрей и солитонов в плазме.
Ур-ние (1) используется не только в теории плазмы, но и при описании многих
др. явлений природы; напр., существует аналогия между дрейфовой турбулентностью
в плазме и турбулентностью волн Рос-сби в атмосферах и океанах планет. В основе
аналогии, роднящей
Большое Красное Пятно в атмосфере Юпитера и дрейфовые вихри в плазме токамака,
лежит схожесть проявления силы Кориолиса во вращающейся планетной атмосфере
и магн. части силы Лоренца в плазме. Как и атм. турбулентность, дрейфовая Т.
п. играет заметную роль в явлениях переноса, приводя к усиленным потокам частиц
и тепла поперёк сильного магн. поля. Существует много диссипативных механизмов
возбуждения дрейфовой турбулентности плазмы, в т. ч. связанных с взаимодействием волн с быстрыми
частицами, инжектируемыми извне или генерируемыми в плазме с помощью дополнит.
нагрева.
Ленгмюровская турбулентность может развиваться в плазме без магн. поля и связана с возбуждением самой
простой моды колебаний в виде смещения электронов относительно ионов (плазменные
колебания). При очень малой амплитуде смещения - это линейные ленгмюровские
волны. Однако при увеличении амплитуды ленгмюровских волн очень быстро возникают
нелинейные эффекты. А именно, вследствие небольшого смещения ионов возникает
модуляционная неустойчивость ,приводящая к появлению сгустков ленгмюровских
волн - солитонов. Эти солитоны оказываются неустойчивыми по отношению к самосжатию
до таких малых размеров (коллапс ленгмюровских волн), что их энергия может переходить
в энергию ускоряемых электронов. Перечисленные выше и многие др. эффекты, обнаруживаемые
в развитой ленгмюров-ской Т. п., описываются ур-ниями Захарова, к-рые следуют
из ур-ний двухжидкостной динамики плазмы при явном выделении в электронном отклике
адиабатической ионной части.
Ленгмюровская Т. п. представляет
собой один из простейших примеров сугубо плазменной турбулентности. Для её развития
существенно движение как электронов, так и ионов. При наличии магн. поля может
развиваться чисто электронная ветвь колебаний при неподвижных ионах - т. н.
геликоны (или свисты), генерируемые в магнитосфере Земли в результате
развития циклотронной неустойчивости или под действием электрич. атм. разрядов.
Геликоны наблюдаются и в полупроводниковой плазме. Др. случай движения электронов
при неподвижных ионах, важный для физики плазменных диодов и размыкателей, а
также для микро- и Z-пинчей, связан с нелинейной динамикой тока в плазме под
действием внешнего и собственного, порождённого током, магн. поля. Вся эта группа
эффектов, в т. ч. и турбулентность соответствующего типа, рассматривается в
рамках т. н. электронной магнитной гидродинамики (ЭМГ).
Ионно-звуковая турбулентность
плазмы. В плазме возможны также турбулентные движения, очень похожие на
обычную турбулентность в газе. Для этого в ней должны быть возбуждены до нелинейного
уровня акустич. ветви колебаний, напр. ионный звук, возбуждаемый током электронов,
имеющих скорость выше нек-рого критич. значения. Ионно-звуковая Т. п. представляет
собой хаос из нелинейно взаимодействующих ионно-звуковых волн. Многие существенные
нелинейные свойства таких волн описываются Кадомцева - Петвиашвили уравнением:
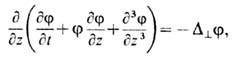
к-рое обобщает Кортевега
- де Фриса уравнение на случай слабонеоднородных волн. Здесь j-электрич.
потенциал плазмы, z - координата вдоль направления распространения волны,
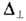 -оператор
Лапласа в поперечной плоскости (все переменные безразмерны). Интересным проявлением
ионно-звуковой Т. п. служит аномальное сопротивление п л а з м ы, возникающее
в ней. поскольку в процессе накачки ионно-звуковой Т. п. электроны передают
свой импульс звуковым волнам.
-оператор
Лапласа в поперечной плоскости (все переменные безразмерны). Интересным проявлением
ионно-звуковой Т. п. служит аномальное сопротивление п л а з м ы, возникающее
в ней. поскольку в процессе накачки ионно-звуковой Т. п. электроны передают
свой импульс звуковым волнам.
Возможные типы Т. п. не
исчерпываются приведёнными выше примерами. Однако при всём разнообразии Т. п.
подчиняется довольно общим закономерностям и складывается из универсальных процессов
нелинейного взаимодействия волн, вихрей и частиц. Это взаимодействие формирует
вид распределения энергии турбулентных пульсаций (спектр турбулентности) и др.
корреляц. характеристики. Если взаимодействие пульсаций является определяющим,
то говорят о сильной турбулентности, если же оно слабо изменяет их спектральные
характеристики, то имеет место слабая турбулентность.
Слабая турбулентность может развиваться в условиях, когда возбуждается много волн небольшой амплитуды
в среде с дисперсией. В результате взаимодействия таких волн их фазы сбиваются,
так что становится применимым приближение хаотич. фаз. Процессы взаимодействия
волн можно также представить в виде разложения по степеням соответствующих нелинейных
членов. Наинизший порядок по амплитуде взаимодействия описывается т. н. квазилинейным
приближением (см. Квазилинейная теория плазмы ),когда учитывается только
индуцированное черенков-ское излучение и поглощение волн резонансными частицами,
скорость к-рых близка к фазовой скорости соответствующей волны (при наличии
магн. поля сюда добавляется ещё излучение и поглощение на гармониках циклотронной
частоты с учётом нормального или аномального эффекта Доплера). Однако в квазилинейном
приближении пренебрегают взаимодействием между волнами (т. е. поток энергии
по спектру отсутствует), поэтому оно является недостаточным для описания действительно
турбулентных процессов. В следующем порядке - возмущений теории - учитываются
процессы, квадратичные по интенсивности волн, приводящие к перекачке энергии
по спектру: индуцированное рассеяние волн на частицах и трёхвол-новые процессы
типа слияния двух волн в одну и распада одной волны на две. Чтобы соответствующие
процессы имели место, должны выполняться резонансные условия распада в виде
равенств
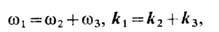
где wi-частоты,
ki-волновые векторы плоских взаимодействующих волн.
Эти условия выполнимы не для всех типов волн в плазме (напр., не выполняются
для волн, фазовая скорость к-рых убывает с увеличением волнового вектора), поэтому
важными могут оказаться четырёхволновые
процессы, учитываемые в более высоком порядке разложения по интенсивности волн
и представляющие собой рассеяние волн на волнах (см. Нелинейные явления в
плазме). В слабой турбулентности для описания вышеназванных процессов, по
аналогии с квантовой механикой, вводится понятие о квазичастицах - плазмонах симпульсом 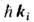 и энергией
и энергией 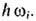 Число плазмонов Nk в единице объёма в интервале волновых векторов
от k до k + dk пропорционально спектральной
функции Ikw, описывающей распределение энергии пульсаций
по спектру турбулентности. В слабой турбулентности частотная зависимость Ikw
близка к d-образной. В этом случае Nk описывается кинетическим
ур-нием волн вида
Число плазмонов Nk в единице объёма в интервале волновых векторов
от k до k + dk пропорционально спектральной
функции Ikw, описывающей распределение энергии пульсаций
по спектру турбулентности. В слабой турбулентности частотная зависимость Ikw
близка к d-образной. В этом случае Nk описывается кинетическим
ур-нием волн вида
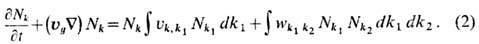
Здесь матричные элементы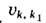 и
и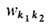 и групповая
скорость плазмонов
и групповая
скорость плазмонов 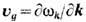 выражаются через компоненты тензора диэлектрич. проницаемости плазмы и фактически
содержат информацию о природе рассматриваемых волн. Выражения для матричных
элементов получаются в результате последовательных итераций поправки к функции
распределения частиц по скоростям и в виде отклика на турбулентные пульсации
эл--магн. поля.
выражаются через компоненты тензора диэлектрич. проницаемости плазмы и фактически
содержат информацию о природе рассматриваемых волн. Выражения для матричных
элементов получаются в результате последовательных итераций поправки к функции
распределения частиц по скоростям и в виде отклика на турбулентные пульсации
эл--магн. поля.
Сильная турбулентность. При увеличении амплитуды пульсаций взаимодействие волн усиливается, матричные
элементы взаимодействия растут и происходит уширение спектра колебаний по частоте,
так что зависимость Ikw от частоты нельзя считать
близкой к d-функции. В таком случае имеет место сильная турбулентность, для
описания к-рой кинетич. ур-ние для волн (2) уже не подходит. Существуют разные
методы рассмотрения сильной турбулентности. Большинство из них основано на идее
перенормировки. Одним из таких подходов является приближение слабой
связи, сходное с приближением прямого взаимодействия в теории гидродинамич.
турбулентности.
П р и б л и ж е н и е с
л а б о й с в я з и. Главным в этом приближении является нахождение перенормированного
(т. е. заранее учитывающего эффекты нелинейного взаимодействия волн в виде дополнит.
коэф. "коллективного" затухания) отклика отдельной волны при её
взаимодействии сразу со всеми волнами. Схематично процедуру такой перенормировки
можно представить на примере модельного ур-ния, типичного для описания плазменной
турбулентности:
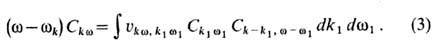
Здесь Ckw
характеризует амплитуду волн, 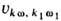 -матричный элемент взаимодействия, wk-собств. частота волны,
следующая из линейного дисперсионного соотношения. Интегральный оператор взаимодействия
в правой части (3) наряду с др. эффектами описывает нелинейное затухание волны,
т. е. содержит члены, пропорциональные её амплитуде
-матричный элемент взаимодействия, wk-собств. частота волны,
следующая из линейного дисперсионного соотношения. Интегральный оператор взаимодействия
в правой части (3) наряду с др. эффектами описывает нелинейное затухание волны,
т. е. содержит члены, пропорциональные её амплитуде 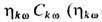 -декремент
коллективного затухания, к-рый и надо определить). Добавляя явно эти члены в
левую и правую части ур-ния (3) и итерируя затем правую часть (см. Итераций
метод), считая её малой (гл. эффект в ней как бы вычтен), приходим к системе
двух ур-ний для спектра
-декремент
коллективного затухания, к-рый и надо определить). Добавляя явно эти члены в
левую и правую части ур-ния (3) и итерируя затем правую часть (см. Итераций
метод), считая её малой (гл. эффект в ней как бы вычтен), приходим к системе
двух ур-ний для спектра 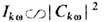 и
перенормированного пропагатора
и
перенормированного пропагатора 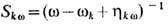 в виде
в виде
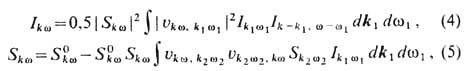
где 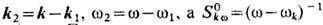 есть пропага-тор (функция Грина отклика плазмы на внеш. воздействие) в линейном
приближении. Интегрирование в (4), (5) проводится по всем возможным волнам,
что приводит к переоценке взаимодействия волн с сильно отличающимися волновыми
векторами и как следствие к неверным (расходящимся) спектрам турбулентности.
На самом деле сильно разномасштабные волны слабо взаимодействуют друг с другом,
не приводя к перекачке энергии по спектру, а лишь смещая более коротковолновый
пакет в пространстве практически без его искажения. Учесть это можно, напр.,
введя подгоночный параметр обрезания x и ограничиваясь в (4), (5) интегрированием
только по волнам с волновыми векторами, отличающимися друг от друга не более
чем в x раз. При этом характеристики спектра в широком диапазоне слабо зависят
от значений x. Из двух ур-ний приближения слабой связи первое как следствие
закона сохранения энергии (суммарная энергия не может измениться в процессе
взаимодействия волн) является точным. Второе ур-ние для нелинейного отклика,
описывающее особенности процесса перераспределения энергии по спектру, является
приближённым. Существуют и др. способы получения ур-ния для нелинейного отклика,
в частности вариационные, когда турбулентность также считается ква-зигауссовской,
а ур-ние для отклика является следствием максимилизации энтропии системы при
тех или иных ограничениях, т. е. является ур-нием Эйлера для вариац. задачи
на условный экстремум. Известен также вариац. способ получения ур-ния непосредственно
для
есть пропага-тор (функция Грина отклика плазмы на внеш. воздействие) в линейном
приближении. Интегрирование в (4), (5) проводится по всем возможным волнам,
что приводит к переоценке взаимодействия волн с сильно отличающимися волновыми
векторами и как следствие к неверным (расходящимся) спектрам турбулентности.
На самом деле сильно разномасштабные волны слабо взаимодействуют друг с другом,
не приводя к перекачке энергии по спектру, а лишь смещая более коротковолновый
пакет в пространстве практически без его искажения. Учесть это можно, напр.,
введя подгоночный параметр обрезания x и ограничиваясь в (4), (5) интегрированием
только по волнам с волновыми векторами, отличающимися друг от друга не более
чем в x раз. При этом характеристики спектра в широком диапазоне слабо зависят
от значений x. Из двух ур-ний приближения слабой связи первое как следствие
закона сохранения энергии (суммарная энергия не может измениться в процессе
взаимодействия волн) является точным. Второе ур-ние для нелинейного отклика,
описывающее особенности процесса перераспределения энергии по спектру, является
приближённым. Существуют и др. способы получения ур-ния для нелинейного отклика,
в частности вариационные, когда турбулентность также считается ква-зигауссовской,
а ур-ние для отклика является следствием максимилизации энтропии системы при
тех или иных ограничениях, т. е. является ур-нием Эйлера для вариац. задачи
на условный экстремум. Известен также вариац. способ получения ур-ния непосредственно
для 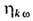 путём
минимизации функционала ошибки при замене точного нелинейного ур-ния (3) ур-нием
Ланжевена с d-коррелированной случайной силой. Предсказываемые этими способами
результаты (константа Колмогорова в спектре турбулентности несжимаемой жидкости
и др.) хорошо согласуются с эксперим. данными.
путём
минимизации функционала ошибки при замене точного нелинейного ур-ния (3) ур-нием
Ланжевена с d-коррелированной случайной силой. Предсказываемые этими способами
результаты (константа Колмогорова в спектре турбулентности несжимаемой жидкости
и др.) хорошо согласуются с эксперим. данными.
Метод подобия. В случае
сильной турбулентности важные результаты могут быть получены в рамках фено-менологич.
методов, одним из к-рых является метод подобия, или размерностный анализ, применённый,
напр., А. Н. Колмогоровым и А. М. Обуховым при изучении спектра пульсаций в
турбулентной жидкости.
В плазме использование
анализа размерностей осложнено одновременным наличием неск. характерных размеров
и времён, из к-рых можно составить неск. безразмерных комбинаций
в виде числовых параметров (напр., число Рейнольдса и т. п.). В этом случае
размерностный анализ приводит к результатам, содержащим произвольные функции от
этих параметров. Тем не менее даже при такой высокой степени произвола размерностный
анализ оказывается полезным, напр. при получении скейлинговых зависимостей времени
удержания термоядерной плазмы от параметров установок.
Один из широко распространённых
методов оценки ко-эф. переноса в плазме, напр., следующий. По аналогии с броуновским
движением частицы считается, что в турбулентном течении регулярное, или скоррелированное,
смещение элементарного объёма плазмы происходит лишь в течение короткого отрезка
времени т, после чего происходит "сбой фазы", а предыдущая история
смещений забывается. Др. словами, т есть время корреляции поля турбулентной
скорости. За это время элемент плазмы смещается на нек-рый характерный размер
r (длина корреляции), зависящий от интенсивности турбулентных пульсаций
скорости и типа скоррелированного движения (оно может быть сложным, напр. не
прямолинейным, а круговым в виде ларморовской орбиты заряж. частицы в магн.
поле и т. д.). Из двух пространственно-временных корреляц. характеристик поля
турбулентной скорости r и t можно составить единственную комбинацию с
размерностью ко-эф. диффузии 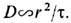 Для оценок величин r и t пользуются след. соображениями. Если турбулентность
не очень сильная и связана с неустойчивостью к--л. колебаний или волн, то в
ней ещё имеют смысл собственные моды и собственные числа соответствующего линейного
(по амплитуде волн) приближения, в частности инкремент g и волновое число
k наиб. неустойчивой волны. За время развития неустойчивости, пропорциональное
1/g наступает нелинейный режим, завершающийся "опрокидыванием" волны.
По аналогии с волнами на поверхности жидкости амплитуду волны в момент её опрокидывания
и, следовательно, величину смещения элементов плазмы r полагают пропорциональными
длине волны, т. е. 1/k. Момент опрокидывания естественно считать моментом
"сбоя фазы", т. е.
Для оценок величин r и t пользуются след. соображениями. Если турбулентность
не очень сильная и связана с неустойчивостью к--л. колебаний или волн, то в
ней ещё имеют смысл собственные моды и собственные числа соответствующего линейного
(по амплитуде волн) приближения, в частности инкремент g и волновое число
k наиб. неустойчивой волны. За время развития неустойчивости, пропорциональное
1/g наступает нелинейный режим, завершающийся "опрокидыванием" волны.
По аналогии с волнами на поверхности жидкости амплитуду волны в момент её опрокидывания
и, следовательно, величину смещения элементов плазмы r полагают пропорциональными
длине волны, т. е. 1/k. Момент опрокидывания естественно считать моментом
"сбоя фазы", т. е. 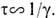 Тогда получается известная оценка
Тогда получается известная оценка 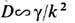 справедливая при не очень высокой амплитуде турбулентных пульсаций. В сильной
турбулентности характер зависимости D от амплитуды пульсаций существенно
меняется, и приходится пользоваться процедурой перенормировки, напр. как в приближении
слабой связи, заранее учитывая турбулентную диффузию в траекториях элементарных
объёмов плазмы. Сложность процессов переноса в сильной турбулентности связана
ещё и с их возможной недиффузи-онностью, когда ср. квадрат смещения l2
пропорционален не t, a tv, с v, отличным от
1/2. Подобная ситуация возникает при наличии в турбулентной
плазме скоррелированных структур в виде "рек" с v=l, попав
в к-рые элемент плазмы совершает т. н. полёты Леви. В сочетании с действительно
диффузионным переносом в остальной "хаотической" части турбулентного
течения это приводит к разл. значениям показателя степени v, к-рые оцениваются
методами теории перколяции (просачивания или проникновения). Примером перколяции
в плазме служит поведение силовых линий магн. поля с хаотич. компонентой. Почти
безынерционные электроны плазмы могут очень быстро смещаться вдоль силовой линии,
так что существуют условия, когда электронный перенос полностью определяется
перколяц. характеристиками магн. поля.
справедливая при не очень высокой амплитуде турбулентных пульсаций. В сильной
турбулентности характер зависимости D от амплитуды пульсаций существенно
меняется, и приходится пользоваться процедурой перенормировки, напр. как в приближении
слабой связи, заранее учитывая турбулентную диффузию в траекториях элементарных
объёмов плазмы. Сложность процессов переноса в сильной турбулентности связана
ещё и с их возможной недиффузи-онностью, когда ср. квадрат смещения l2
пропорционален не t, a tv, с v, отличным от
1/2. Подобная ситуация возникает при наличии в турбулентной
плазме скоррелированных структур в виде "рек" с v=l, попав
в к-рые элемент плазмы совершает т. н. полёты Леви. В сочетании с действительно
диффузионным переносом в остальной "хаотической" части турбулентного
течения это приводит к разл. значениям показателя степени v, к-рые оцениваются
методами теории перколяции (просачивания или проникновения). Примером перколяции
в плазме служит поведение силовых линий магн. поля с хаотич. компонентой. Почти
безынерционные электроны плазмы могут очень быстро смещаться вдоль силовой линии,
так что существуют условия, когда электронный перенос полностью определяется
перколяц. характеристиками магн. поля.
Др. пример феноменологич.
подхода к изучению Т. п., в частности турбулентного переноса, связан с введением
понятия длины перемешивания. Под длиной перемешивания lп обычно
понимают ср. длину взаимного проникновения элементов плазмы (или жидкости) в
турбулентном течении. Если рассматривается турбулентный перенос нек-рой усреднённой
по турбулентным пульсациям величины А вдоль направления её градиента
и если этот градиент влияет на амплитуду турбулентных пульсаций (напр., является
причиной раскачки неустойчивости), то можно предполагать, что и коэф. турбулентного
переноса также зависит от величины градиента 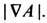
Турбулентность плазмы очень часто включает в себя как чисто хаотич. тип движения, так и
набор разл. самоорганизованных структур, возникающих из хаоса и на его фоне
в процессе нелинейного взаимодействия разл. колебаний, волн, вихрей. Наличие
такого взаимодействия и, следовательно, перекачки энергии по фазовому пространству
системы - непременное и интуитивно понятное условие самоорганизации. Однако
не всякое регулярное течение и (или) равновесие плазмы, возникшее в результате
эволюции первоначально хаотич. состояния, следует рассматривать как самоорганизованное.
Примером служит система невзаимодействующих линейных волн, каждая из к-рых характеризуется
своим временем жизни либо инкрементом нарастания. Даже при хаотич. начальном
распределении параметров спустя достаточное время в такой системе будет доминировать
лишь одна, наиболее неустойчивая либо долгоживущая, волна, воспринимаемая как
довольно регулярная структура. Между тем ясно, что такая эволюция не является
процессом самоорганизации, в к-ром хаотич. и регулярная компоненты принципиально
связаны друг с другом. Эту связь грубо, но наглядно можно представить как перераспределение
энтропии между разл. областями фазового пространства системы. Самоорганизация
(локальное уменьшение энтропии) в одной группе параметров и масштабов сопровождается
дезорганизацией (ростом энтропии) в других на фоне общего возрастания энтропии
вследствие всегда реально присутствующей диссипации. Подобная трактовка характерна
для целого ряда т. н. энтропийных подходов к явлению самоорганизации, когда
считается, что турбулентное течение эволюционирует к состоянию с максимальной
полной энтропией при условии сохранения к--л. интегральных характеристик. Это
означает максимально возможную потерю информации о нач. состоянии системы, но
всё же при условии запоминания нек-рых её свойств. То, что система "о
себе помнит", математически формулируется как соответствующий закон сохранения
(интеграл движения или идеальный инвариант). Наличие таких инвариантов определяет
вид функции распределения вероятности Р нахождения системы в к--л. состоянии
(к--л. точке фазового пространства) как результат решения соответствующей ва-риац.
задачи на условный экстремум. В отсутствие интегралов движения максимизация
энтропии приводит к равнораспределению, когда все состояния равновероятны. При
сохранении только полной энергии системы максимум энтропии осуществляется при
нормальном (гауссов-ском) распределении Р. При более разнообразном наборе
интегралов движения вид Р может заметно отличаться от гауссовского, что,
как известно, приводит к появлению долгоживущих крупномасштабных "самоорганизованных"
структур. При этом Р оказывается чувствительным к используемому набору
инвариантов и возникает вопрос о правомерности сделанного выбора "существенных"
интегралов движения. Большинство последних сохраняется лишь в отсутствие диссипации
и не является, строго говоря, инвариантами в реальных течениях. Однако разрушение
этих интегралов происходит разными темпами, на разных временных шкалах, что
и позволяет классифицировать все возможные идеальные инварианты как долгожи-вущие
("существенные") либо быстро разрушающиеся. Эволюцию турбулентности
при этом естественно рассматривать как релаксацию к состоянию с мин. значением
быстро распадающихся инвариантов при условии постоянства долгоживущих.
Успешным применением такого
подхода к самоорганизации является теория Тейлора, объясняющая эффект генерации
магн. поля в плазме с МГД турбулентностью. В идеальной сверхпроводящей плазме,
как известно, сохраняются энергия 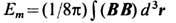 и спиральность
и спиральность 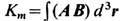 магн. поля, где А есть векторный потенциал, т. е.
магн. поля, где А есть векторный потенциал, т. е.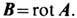 Величина Кт характеризует топологию магн. силовых линий и
может изменяться только в процессе их пересоединения. Если кол-во таких пересоединений
в единице объёма не слишком велико, т. е. магн. поле не очень "запутано",
то Ет диссипирует значительно быстрее, чем Кт. Следовательно, релаксированное состояние плазмы характеризуется мин. значением
Ет при постоянстве Кт. Соответствующая вариац.
задача приводит к известной бессиловой конфигурации B= a rotA
где константа a находится по нач. значениям Кт и граничным
условиям для плазмы. При определ. значениях Кт получается
конфигурация с разным направлением магн. силовых линий на оси и на периферии
плазменного тороида, что соответствует экспериментально наблюдаемой структуре
магн. поля в пинчах с обращённым магн. полем.
Величина Кт характеризует топологию магн. силовых линий и
может изменяться только в процессе их пересоединения. Если кол-во таких пересоединений
в единице объёма не слишком велико, т. е. магн. поле не очень "запутано",
то Ет диссипирует значительно быстрее, чем Кт. Следовательно, релаксированное состояние плазмы характеризуется мин. значением
Ет при постоянстве Кт. Соответствующая вариац.
задача приводит к известной бессиловой конфигурации B= a rotA
где константа a находится по нач. значениям Кт и граничным
условиям для плазмы. При определ. значениях Кт получается
конфигурация с разным направлением магн. силовых линий на оси и на периферии
плазменного тороида, что соответствует экспериментально наблюдаемой структуре
магн. поля в пинчах с обращённым магн. полем.
Поскольку при классификации
инвариантов как долго-живущих и быстро разрушающихся важны лишь относительные
масштабы времени изменения интегральных характеристик плазмы, то совершенно
не обязательно принимать в расчёт только идеальные интегралы движения. В качестве
долгоживущего "инварианта" можно принимать физически осмысленную
и обоснованную интегральную характеристику, лишь бы она действительно, по тем
или иным причинам, поддерживалась постоянной или изменялась медленнее др. интегралов.
Примером самоорганизации в таких условиях служит установление самосогласованных
профилей плотности тока и давления в плазме токамака в широком диапазоне параметров
разряда и условий ввода. мощности в плазму. Если считать, что полный ток в разряде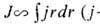 -плотность тока) фиксирован хотя бы и внеш. причинами, тогда как полная энергия
плазмы, магнитная и тепловая
-плотность тока) фиксирован хотя бы и внеш. причинами, тогда как полная энергия
плазмы, магнитная и тепловая 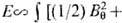
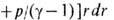 (р - давление плазмы, g-показатель адиабаты,
(р - давление плазмы, g-показатель адиабаты, 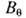 -
полоидальное магн. поле), диссипирует, то соответствующая вариац. задача приводит
к "универсальному" профилю коэффициента запаса устойчивости
-
полоидальное магн. поле), диссипирует, то соответствующая вариац. задача приводит
к "универсальному" профилю коэффициента запаса устойчивости 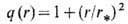 к-рый в грубых чертах согласуется с экспе-рим. наблюдениями.
к-рый в грубых чертах согласуется с экспе-рим. наблюдениями.
К самоорганизованным состояниям относятся и двойные слои в ленгмюровской плазме. Они наблюдаются в ионосферной и космич. плазме в виде долгоживущих самоподдерживающихся пространств. скачков электростатич. потенциала с амплитудой значительно выше теплового уровня, а также в лаб. плазме электродных разрядов в виде виртуальных катодов внутри столба плазмы. Двойные слои возникают на нелинейной стадии неустойчивости ленгмюровских возмущений. Такие структуры лас-то сопровождаются образованием "дыр" в фазовом пространстве, т. е. областей, свободных от частиц. В фазовом пространстве одномерного движения кроме дыр могут существовать и др. когерентные структуры - клампы, похожие на вихри в обычной жидкости с захваченными в них частицами (см. Солитон в плазме). Зарождение и движение таких "вихрей" по фазовому пространству является важным моментом в динамике самоорганизованной турбулентности.

С. В. Базденков, Б. Б. Кадомцев
Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.
|
|