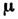(аксиальный вектор), на больших расстояниях от
системы создаёт магнитное полеСогласно представлениям классической электродинамики, магнитное поле создаётся движущимися электрическими зарядами. Так как магнитное поле по своей природе является вихревым, то в нем отсутствуют полюса и гипотетические магнитные монополи. Поэтому элементарной характеристикой магнитных свойств оказывается именно магнитный момент.
Система, обладающая магнитным моментом 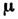(аксиальный вектор), на больших расстояниях от
системы создаёт магнитное поле
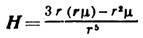
(r - радиус-вектор точки наблюдения). Аналогичный вид имеет электрическое поле диполя,
состоящего из двух близко расположенных электрических зарядов противоположного знака.
Однако, в отличие от электрического дипольного момента магнитный момент создаётся не системой
точечных "магнитных зарядов", а электрическими токами, текущими внутри системы.
Если замкнутый электрич. ток плотности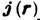 
течёт в ограниченном объёме V, то создаваемый им магнитный момент
определяется формулой
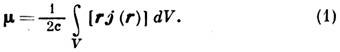
В простейшем случае замкнутого кругового тока I, текущего
вдоль плоского витка площади s,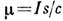 
,
причём вектор магнитного момента направлен вдоль правой нормали к витку.
Если ток создаётся стационарным движением точечных электрических зарядов
с массами
, имеющими скорости
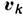, то возникающий магнитный момент,
как следует из формулы (1), имеет вид
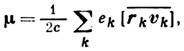
где подразумевается усреднение микроскопических величин по времени.
Поскольку стоящее в правой части векторное произведение пропорционально
вектору момента количества движения частицы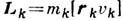 
(предполагается, что скорости 
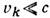), то вклады отдельных частиц в магнитный момент и в
момент количества движения оказываются пропорциональными:
Коэффициент пропорциональности е/2тс называется гиромагнитным отношением; эта величина
характеризует универсальную связь между магнитными и механическими свойствами
заряженных частиц в классической электродинамике.
Однако движение элементарных носителей заряда в веществе (электронов) подчиняется
законам квантовой механики,
вносящей коррективы в классическую картину. Помимо "орбитального" механического
момента количества движения L электрон обладает внутренним механическим
моментом - спином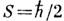 
.
Полный магнитный момент электрона равен сумме орбитального М. м. (2) и спинового
магнитного момент.
Как видно из этой формулы (вытекающей из Дирака уравнения для электрона), гиромагного
отношение для спина оказывается ровно в два раза больше, чем для орбитального
момента. Особенностью квантового представления о магнитном и механическом моментах является
также то, что векторы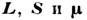 
не могут иметь определённого направления в пространстве вследствие некоммутативности
операторов проекции этих векторов на оси координат.
Спиновый магнитный момент заряженной частицы, определяемый формулой (3),
называется нормальным, для электрона он равен магнетону Бора. Опыт показывает, однако, что
магнитный момент электрона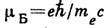 
отличается от (3) на величину порядка 
(
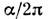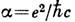- постоянная
тонкой структуры). Подобная добавка, называемая аномальным магнитным моментом, возникает вследствие взаимодействия электрона с фотонами, она описывается
в рамках квантовой электродинамики. Аномальными магнитными моментами
обладают и другие элементарные частицы; особенно велики они для
адронов, которые, согласно современным
представлениям, имеют внутреннюю структуру. Так, аномальный магнитный момент
протона в 2,79 раза больше "нормального" - ядерного магнетона,
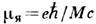(М - масса протона),
а магнитный момент нейтрона равен -1,91
,
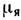т. е. существенно отличен от нуля, хотя нейтрон не обладает электрическим зарядом.
Такие большие аномальные магнитные моменты адронов обусловлены внутр. движением входящих
в их состав заряженных эфирных доменов.
|
|
 |
